Download 6.1/6.2/6.3 Solving Inequalities

1-5 Solving
Inequalities
Solving inequalities by
addition, subtraction,
multiplication, and division
Remember: Inequality Signs
<
-- Less than
> -- Greater than
≤ -- Less than or Equal to
≥ -- Greater than or Equal to
Graph an Inequality in One
Variable
x
<2
z
≤1
a
> -2
0
≤d
Remember
 Open
circle represents everything up to
that value but does not include it.
 Closed circle represents everything up to
that value and that value itself.
 Use open circle for < and >.
 Use closed circle for ≤ and ≥.
Ok… now you try
Linear Equations v. Linear
Inequalities
•
•
There are many characteristics between
inequalities and equations that are very similar…
Then again there are differences also…
Linear Equations v. Linear
Inequalities
 Equations
have
equal signs
 Equations generally
have only one
solution.
 We undo
operations in order
to solve equations.
 Inequalities
use
inequality signs.
 Inequalities
represent infinite
solutions
 We undo
operations in order
to solve
inequalities.
Solving Equations is very similar
to solving Inequalities…
𝑥 + 4 = 7
𝑥+ 4– 4 = 7 − 4
𝑥 = 3
𝑥 + 4 ≥ 7
𝑥 + 4– 4 ≥ 7 − 4
𝑥 ≥ 3
Solving Equations is very similar
to solving Inequalities…
−2 = 𝑛 − 4
−2 + 4 = 𝑛 – 4 + 4
2 = 𝑛
𝑛 = 2
−2 > 𝑛 − 4
−2 + 4 > 𝑛 – 4 + 4
2 > 𝑛
𝑛 < 2
Set Builder Notation
 The
Solution n < 2
states that set of all
numbers less then
2 are solutions to
the Inequality in
the Example.
 Another
way to
represent n < 2 is in
set builder
notation.
 {n | n < 2}
You try…
1.
d+4≤6
𝑑 𝑑 ≤ 2}
4.
-2≥h+6
ℎ ℎ ≤ −8}
2.
x–3>2
5.
- 5 ≤ -5 + s
3.
𝑥 𝑥 > 5}
q + 12 ≥ 4
6.
𝑠 𝑠 ≥ 0}
2v > v - 3
𝑞 𝑞 ≥ −8}
𝑣 𝑣 > −3}
6.2
Investigating
Inequalities
Developing Concepts
•
How do operations
affect an Inequality
Create your own!
 Create
any inequality you want that is
TRUE!
 Use either < or >!
Fill in the table with your
inequality…
Think about it…
 Would
I flip the inequality sign if…
6.2 Solving Inequalities by
using Multiplication and
Division
•
To solve one step inequalities in one variable
using multiplication or division.
Look at the symbols!
Properties of Inequalities with
Multiplication/Division…
 When
Multiplying or Dividing both sides by
a positive number (𝑛 > 0)…
 Keep the Inequality sign the way it is.
 When multiplying or dividing both sides
by a negative number (𝑛 < 0)…
 Flip the Inequality sign…
Properties of Inequalities with
Division…
 When
dividing both
sides by a positive
number…
 Keep the Inequality
sign the way it is.
 When
dividing both
sides by a negative
number…
 Flip the Inequality
sign…
Look at the symbols!
Solve
𝑥
< −2
4
𝑥
(4) < −2(4)
4
Multiplied by
Positive
𝑥 < −8
𝑥
<6
−3
𝑥
(−3)
< −2(−3)
−3
Multiplied by
Negative
𝑥>6
Solve…
−20 ≤ 4𝑥
−20 4𝑥
≤
4
4
−5 ≤ 𝑥
𝑥 ≥ −5
20 ≤ −4𝑥
20 −4𝑥
≤
−4
−4
−5 ≥ 𝑥
𝑥 ≤ −5
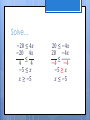
You Try…

≤ -4
 -5

≤
≤3
 <
-10
 5x
≤ -15
 -30
< -6x
 -3x
<9
 9x
> -3
What about Fractions that are
Coefficients?
1
x > -6
2
2 1
2
( ) x > -6( )
1 2
1
x > -12
2
3
2
3
- x > 18
(-
3
)2
x > 18(-
X < -27
3
)
2
Try this…
6.3 Solving
Multi-Step
Inequalities
Goal:
Solving multistep
Inequalities in one variable
What is a Multi-Step
Inequality?
A
Multi-Step
Inequality is just like
a Multi-Step
Equation. It takes
more than one
step to solve.
Solve Inequalities/Equations
 Solve…
2y – 5 < 7
2y – 5 + 5 < 7 + 5
2y < 12
2𝑦
12
<
2
2
y<6
 Think…
2y – 5 = 7
2y – 5 + 5 = 7 + 5
2y = 12
2𝑦
12
=
2
2
y=6
Solve…
 Solve…
-5 – x > 4
-5 – x + 5 > 4 + 5
-x > 9
(-1) –x > 9 (-1)
x < -9
 Think…
-5 – x = 4
-5 – x + 5 = 4 + 5
-x = 9
(-1) –x = 9 (-1)
x = -9
You try…
1.
3x – 5 > 4
3.
-4 < y or y > -4
x>3
2.
10 – n ≤ 5
n≥5
13 > - 3 - 4y
4.
𝑥
4
+6≥5
x ≥ -4
Using the Distributive
Property…
 Solve…
3(x + 2) < 7
3x + 6 < 7
3x + 6 - 6 < 7 – 6
3x < 1
<
x <
Try…
 3(n
– 4) ≥ 6
 -2(x
+ 1) < 2
What if there were two
variables?
2x – 3 ≥ 4x + 1
2x – 3 – 2x ≥ 4x + 1 - 2x
-3 ≥ 2x + 1
-3 - 1 ≥ 2x + 1 – 1
-4 ≥ 2x
−4 2𝑥
≥
2
-2 ≥ x
x ≤ -2
2
You try…
 5n
X
– 21 < 8n + 6
+ 3 ≥ 2x - 4
 4y
-
– 3 < -y + 12
3z + 15 > 2z
Solve the Equations!
4x+8 = 4(x+2)
4x + 8 = 4x + 8
4x + 8 – 4x = 4x + 8 – 4x
8=8
Infinite Solutions
Or
Identity
2x+10 = -2(-x + 5)
2x+10 = 2x - 10
2x + 10 - 2x = 2x - 10 - 2x
10 = -10
10 ≠ -10
No Solutions
Unbalanced!
What about if the variables
eliminate each other?
 Solve
4x+8 > 4(x+2)
4x + 8 > 4x + 8
4x + 8 – 4x > 4x + 8 – 4x
8>8
N/S!
 This
inequality
will not work
because my
end statement is
NOT TRUE!
 What if the sign
was ≥ ?
Lets Try…
2x+6 ≤ 2(x-3)
2x+6 ≤ 2x-6
2x+6 – 2x ≤ 2x-6 – 2x
6 ≤ -6
This is an untrue inequality!
Therefore there is No Solutions to this
Inequality!
Now Try…
2(x + > x - 4
x+>x–4
x+-x>x–4-x
>–4
This is a true inequality!
Therefore any solution for x will work.
It has Infinite Solutions.
1.) 2𝑥 + 5 − 6𝑥 > −4(𝑥 + 5)
5 > -20
TRUE! Infinite Solutions!
2. ) 4 𝑥 − 2 ≥ −2 (4 − 2𝑥)
-8
3.)
≥ -8
TRUE! Infinite Solutions!
2x + 4 > 5x – 2
2 > x or x < 2
4.)
5( 1 – x ) ≤ -1( 5x + 10)
5 ≤ - 10
FALSE! NO SOLUTIONS