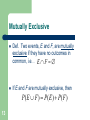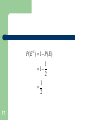Download Basic Probability- Power point

Definitions
Experiment – a process by which an observation
( or measurement ) is observed



Sample Space (S)- The set of all possible outcomes
(or results) of an experiment
Event (E) – a collection of outcomes
i.e E  S
1
Example
Experiment : Toss a balanced die once and
observe its uppermost face
Sample Space =S={1,2,3,4,5,6}
Events: 1.observe a even number
E= { 2,4,6}
2. observe a number less than or
equal to 4
F= { 1,2,3,4}
2
Probability


Given a event (E) , we would like to assign it a
number, P(E)
P(E) is called the probability of E (likelihood that E
will occur)
0  P( E )  1

3
Practical Interpretation
The fraction of times that E happens out of a huge
number of trials of the same experiment will be close
to P(E)
Types of Probabilities


4
Theoretical
Empirical
Theoretical Probabilities


Used if the outcomes of an experiment are
equally likely to occur
If E is an Event
number of outcomes in event E
P( E ) 
number of outcomes in sample space
5
Example
Toss a balanced die once and observe its
uppermost face
S={1,2,3,4,5,6}
Let G=“observe a number divisible by 3”
G={3,6}
Then P(G)=2/6=1/3

6
Empirical Probabilities



Used when theoretical probabilities cannot be
used
The experiment is repeated large number of
times
If E is an Event
number of times E happens
P( E ) 
number of trials
7
Example
The freshman class at ABC college
- 770 students
- 485 identified themselves as “smokers”
Compute the empirical probability that a
randomly selected freshman student from
this class is not a smoker

8
Example-contd.
9

E= event that a randomly chosen student
from this class is not a smoker

P(E)= 285/770=0.37
Properties I
1. 0  P ( E )  1
P( E )  1
2. If E is certain to happen
3. If E and F cannot both happen
P( E or F )  P( E )  P( F )
4.
10
P( S )  1
Union
Def. The union of two sets, E and F, is the
set of outcomes in E or F .
 Example:
E= { 2,4,6}
F= { 1,2,3,4}

E  F  {1, 2, 3, 4, 6}
11
Intersection
Def. The intersection of two sets, E and F, is the
set of outcomes in E and F .
 Example:
E= { 2,4,6}
F= { 1,2,3,4}

E  F  {2 ,4}
12
Mutually Exclusive

Def. Two events, E and F, are mutually
exclusive if they have no outcomes in
common, i.e. . E  F  

If E and F are mutually exclusive, then
P( E  F )  P( E )  P( F )
13


This property can be extended to more than
two events.
For any two events, E and F,
P( E  F )  P( E )  P( F )  P( E  F )
14
Complement of an Event



Def. The complement of an event, E, is the event
that E does not happen .
Example: S={1,2,3,4,5,6}
E= { 2,4,6}
E  {1 ,3 ,5}
C
 Does E and E have common outcomes?
C
15

Since the two events are Mutually Exclusive
P( E  E C )  P( E )  P( E C )
P( S )  P( E )  P( E C )
1  P( E )  P( E )
C
P( E C )  1  P( E )
16
P( E C )  1  P( E )
1
 1
2
1

2
17




18
Assign probability to each outcome
Each probability must be between 0 and 1
The sum of the probabilities must be equal to 1
If the outcomes of an experiment are all equally
likely, then the probability of each outcome is given
by 1 ,where n is the number of possible outcomes
n
DeMorgan’s Laws
P( E C  F C )  P(( E  F )C )  1  P( E  F )
P( E C  F C )  P(( E  F )C )  1  P( E  F )
19
Project Focus
• How can probability help us with the
decision on whether or not to attempt a loan work out?
Events:
S- an attempted work out is successful
F- an attempted work out fails
Goal:
P(S) – Probability of S or fraction of past work out arrangements which
were successful
P(F) - Probability of F or fraction of past work out arrangements which
were unsuccessful?
20
Using “Countif” function in Excel


1.
2.
21
Counts the number of cells within a given
range that meets the given criteria
Fields for the function
Range
Criteria
Project Focus – Basic Probability
Counting
Fractions
Number of Number of Fraction of Fraction of
Successes Failures Successes Failures
3,818
4,408 0.464138099 0.535861901
22
Estimated Probabilities
P (S )
0.464
P (F )
0.536
More on Events S & F

F is the complement of S
Recall:
P( S C )  1  P( S )
P( F )  1  P( S )
23