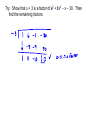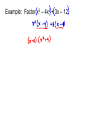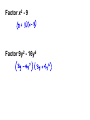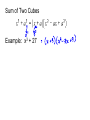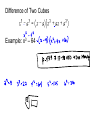* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Remainder and Factor Theorems
Survey
Document related concepts
Transcript
Remainder and Factor Theorems Divide f(x) = 4x2 – 3x + 6 by x – 2. Long Division What is f(2)? Synthetic Division In the previous problem, the value of f(2) was the same as the remainder when dividing by x – 2. This illustrates the Remainder Theorem. • When synthetic division is used to evaluate a function, it is called synthetic substitution. • It is convenient when the degree of the polynomial is greater than 2. • When you divide a polynomial by one of its binomial factors, the result is called a depressed polynomial. • If the remainder is 0 after completing division, then x – a is a binomial factor of the polynomial, and a is a zero. This is a special case of the Remainder Theorem, called the Factor Theorem. • To show that a binomial is a factor of a polynomial, we want to show that the remainder is 0 after division. • We can then find the remaining zeros or roots of the polynomial using quadratic methods. Example: Show that x – 3 is a factor of x3 + 4x2 – 15x – 18. Then find the remaining factors. Try: Show that x + 3 is a factor of x3 + 6x2 – x – 30. Then find the remaining factors. Factoring Grouping, Special Cases • If you have 4 or more terms, you group terms together so that they will have a common factor. • Factor each group separately. • You will then be able to factor over the entire expression. • Rewrite. Example: Factor x3 + 5x2 – 2x – 10 Example: Factor x3 – 4x2 + 3x – 12 Example: Factor 3x3 + 2xy – 15x2 – 10y Difference of Two Squares You may remember seeing expressions like this one when you worked with multiplying algebraic expressions. Do you remember ... If you remember this fact, then you already know that the factors of are and Remember: An algebraic term is a perfect square when the numerical coefficient (the number in front of the variables) is a perfect square and the exponents of each of the variables are even numbers. Factor x2 - 9 Factor 9y2 - 16y6 Sum of Two Cubes Example: x3 + 27 Difference of Two Cubes Example: x3 – 64 What about x6 – y6 ?