Download Bend it Like Magnus: An Inspection of the Magnus Effect in Soccer

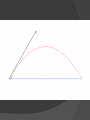
Michal Nowicki Edwin Perezic Zachary Conrad
Outline
Basic Understanding of Effect
Physical Examples
1.
1.
2.
Projectile Motion
Roberto Carlos 1997, Occidental Soccer 2015
Physics of effect
2.
1.
Fluid Dynamics and Aerodynamics
Mathematics of Movement
3.
1.
2.
3.
ODEs of projectile motion
Numerical Method for Solution: Runge-Kutta
Method
Mathematica Modeling of solution
Introduction to Projectile Motion
x = xo+vxot
y=0
z = zo+ vzot – ½gt2
x -> displacement in x direction
y -> displacement in y direction
z -> displacement in z direction
g -> gravity constant
v -> initial velocity
Physical Examples

Roberto Carlos 1997

Basketball
Fluid Dynamics
• Real world is not a vacuum
• Drag force and lift force
• Fl=-.5p|v|2Cl
• Lift coefficient
• Depends on spin
• Additional curvature of trajectory
ODEs of Projectile Motion
x -> displacement in x direction
y -> displacement in y direction
z -> displacement in z direction
kd -> drag coeffecient
g -> gravity constant
kl -> lift coeffecient
γ -> angle between spin axis and ground plane (x,y plane)
v -> initial velocity
Runge-Kutta Numerical Method

Essentially a modified Eulers Method
 Weighted Averages
Method used by Mathematica to solve
ODEs
 For all three equations in the ODE

 x(t0)=0
 y(t0)=0
 z(t0)=0
Runge-Kutta Cont.
y’= f(t,y)
y(t0)= n0
t0=0
Timestep= h
k1=hf(t0,n0)
k2=hf(t0+h/2,n0+k1/2)
k3=hf(t0+h/2,n0+k2/2)
k4=hf(t0+h,n0+k3)
n1=n0+(k1+2k2+2k3+k4)
6
Mathematica

Due to complexity of the system of
ODEs we used Mathematica to solve
and model this system
Conclusion
Gained understanding of the effect of
the Magnus Effect on the flight of a
soccer ball
 Found ODEs for motion of a soccer ball
 Used Mathematica model to solve the
ODEs of flight of a soccer ball
 Modeled famous free kicks such as
Roberto Carlos 1997 using Mathematica
