Download 6-2 Parallelograms 6-4 Rectangles

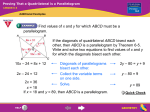
Advanced Geometry
Polygons
Lesson 3
Tests for Parallelograms
There are 5 ways to prove that a quadrilateral is a
parallelogram.
•
Definition of parallelogram
•
If both pairs of opposite sides of a quadrilateral are congruent,
then the quadrilateral is a parallelogram.
•
If both pairs of opposite angles of a quadrilateral are congruent,
then the quadrilateral is a parallelogram.
•
If the diagonals of a quadrilateral bisect each other, then the
quadrilateral is a parallelogram.
•
If one pair of opposite sides of a quadrilateral is both parallel
and congruent, then the quadrilateral is a parallelogram.
Example:
Determine whether each quadrilateral is a
parallelogram. Justify your answer.
Parallelogram
Each pair of opposite
angles is congruent.
Example:
Write a proof of the statement:
If a diagonal of a quadrilateral divides the quadrilateral
into two congruent triangles, then the quadrilateral is a
parallelogram.
Example:
Determine whether a figure with the given vertices is a
parallelogram. Use the method indicated.
A(-3, 0), B(-1, 3), C(3, 2), D(1, -1); Slope Formula
Method:
Parallelogram Test:
Slope Formula
Def. of parallelogram
-Test to see if opposite sides are parallel.
Midpoint Formula
Diagonals bisect each other.
-Find the midpoint of each diagonal to make
sure it is the same point.
Distance Formula
Opposite sides are congruent.
-Find the length of each side to make sure
opposite sides have the same lengths.
Distance & Slope
Formulas
One pair of opposite sides are both parallel
and congruent.
-Find the lengths and slopes of the same pair
of opposite sides.
Example:
Determine whether a figure with the given vertices is a
parallelogram. Use the method indicated.
F(-2, 4), G(4, 2), H(4, -2), F(-2, -1); Distance and Slope Formulas