Download 31_InstructorSolutionsWin

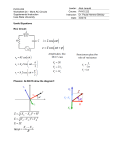
31
ALTERNATING CURRENT
31.1.
IDENTIFY:
i  I cost and I rms  I/ 2.
SET UP: The specified value is the root-mean-square current; I rms  0.34 A.
EXECUTE: (a) I rms  0.34 A
31.2.
(b) I  2I rms  2(0.34 A)  0.48 A.
(c) Since the current is positive half of the time and negative half of the time, its average value is zero.
2
 (0.34 A)2  0.12 A 2.
(d) Since I rms is the square root of the average of i 2, the average square of the current is I rms
EVALUATE: The current amplitude is larger than its rms value.
IDENTIFY and SET UP: Apply Eqs.(31.3) and (31.4)
EXECUTE: (a) I  2I rms  2(2.10 A)  2.97 A.
(b) I rav 
31.3.
31.4.
2

I
2

(2.97 A)  1.89 A.
EVALUATE: (c) The root-mean-square voltage is always greater than the rectified average, because squaring the
current before averaging, and then taking the square root to get the root-mean-square value will always give a
larger value than just averaging.
IDENTIFY and SET UP: Apply Eq.(31.5).
V
45.0 V
EXECUTE: (a) Vrms 

 31.8 V.
2
2
(b) Since the voltage is sinusoidal, the average is zero.
EVALUATE: The voltage amplitude is larger than Vrms .
IDENTIFY:
V  IX C with X C 
1
C
.
 is the angular frequency, in rad/s.
I
EXECUTE: (a) V  IX C 
so I  V C  (60.0 V)(100 rad s)(2.20 106 F)  0.0132 A.
C
(b) I  V C  (60.0 V)(1000 rad s)(2.20 106 F)  0.132 A.
SET UP:
(c) I  V C  (60.0 V)(10,000 rad s)(2.20 106 F)  1.32 A.
(d) The plot of log I versus log is given in Figure 31.4.
EVALUATE: I  VC so log I  log(VC)  log. A graph of log I versus log should be a straight line with
slope +1, and that is what Figure 31.4 shows.
Figure 31.4
31-1
31-2
31.5.
Chapter 31
IDENTIFY: V  IX L with X L   L .
SET UP:  is the angular frequency, in rad/s.
V
60.0 V

 0.120 A.
EXECUTE: (a) V  IX L  I L and I 
 L (100 rad s)(5.00 H)
(b) I 
V
60.0 V

 0.0120 A .
 L (1000 rad s)(5.00 H)
(c) I 
V
60.0 V

 0.00120 A .
 L (10,000 rad s)(5.00 H)
(d) The plot of log I versus log is given in Figure 31.5.
EVALUATE:
I
V
L
so log I  log(V / L)  log . A graph of log I versus log should be a straight line with
slope 1, and that is what Figure 31.5 shows.
Figure 31.5
31.6.
IDENTIFY: The reactance of capacitors and inductors depends on the angular frequency at which they are
operated, as well as their capacitance or inductance.
SET UP: The reactances are X C  1/ C and X L   L .
EXECUTE: (a) Equating the reactances gives  L 
(b) Using the numerical values we get  
31.7.
1
C

1
LC
1
1
= 7560 rad/s

LC
(5.00 mH)(3.50 µF)
XC = XL = L = (7560 rad/s)(5.00 mH) = 37.8 Ω
EVALUATE: At other angular frequencies, the two reactances could be very different.
IDENTIFY and SET UP: For a resistor vR  iR. For an inductor, vL  V cos(t  90°). For a capacitor,
vC  V cos(t  90°).
EXECUTE: The graphs are sketched in Figures 31.7a-c. The phasor diagrams are given in Figure 31.7d.
EVALUATE: For a resistor only in the circuit, the current and voltage in phase. For an inductor only, the voltage
leads the current by 90°. For a capacitor only, the voltage lags the current by 90°.
Figure 31.7a and b
NAlternating Current
31-3
Figure 31.7c
Figure 31.7d
31.8.
IDENTIFY: The reactance of an inductor is X L   L  2 fL . The reactance of a capacitor is X C 
1
C

1
.
2 fC
SET UP: The frequency f is in Hz.
EXECUTE: (a) At 60.0 Hz, X L  2 (60.0 Hz)(0.450 H)  170 . X L is proportional to f so at 600 Hz, X L  1700 .
(b) At 60.0 Hz, X C 
1
 1.06 103 . X C is proportional to 1/ f , so at 600 Hz, X C  106 .
2 (60.0 Hz)(2.50  106 F)
(c) X L  X C says 2 fL 
31.9.
EVALUATE: X L increases when f increases. X C increases when f increases.
IDENTIFY and SET UP: Use Eqs.(31.12) and (31.18).
EXECUTE: (a) X L   L  2 fL  2 (80.0 Hz)(3.00 H)  1510 
(b) X L  2 fL gives L 
(c) X C 
(d) X C 
1
C
IDENTIFY:
SET UP:
1
1

 497 
2 fC 2 (80.0 Hz)(4.00 106 F)
X L increases when L increases; X C decreases when C increases.
VL  I L
 is the angular frequency, in rad/s. f 

is the frequency in Hz.
2
VL
(12.0 V)

 1.63  106 Hz.
2 IL 2 (2.60  103 A)(4.50  104 H)
EVALUATE: When f is increased, I decreases.
IDENTIFY and SET UP: Apply Eqs.(31.18) and (31.19).
V
170 V
EXECUTE: V  IX C so X C  
 200 
I 0.850 A
1
1
1
XC 
gives C 

 1.33 105 F  13.3  F
C
2 f X C 2 (60.0 Hz)(200 )
EVALUATE: The reactance relates the voltage amplitude to the current amplitude and is similar to Ohm’s law.
EXECUTE:
31.11.

XL
120 

 0.239 H
2 f 2 (80.0 Hz)
1
1
1
gives C 

 1.66 105 F
2 fC
2 f X C 2 (80.0 Hz)(120 )
EVALUATE:
31.10.
1
1
1
and f 

 150 Hz.
2 fC
2 LC 2 (0.450 H)(2.50 106 F)
VL  I L so f 
31-4
Chapter 31
31.12.
IDENTIFY: Compare vC that is given in the problem to the general form vC 
I
sin t and determine  .
C
1
. vR  iR and i  I cos.
C
1
1

 1736 
EXECUTE: (a) X C 
 C (120 rad s)(4.80 106 F)
V
7.60 V
 4.378 103 A and i  I cos  t  (4.378  103 A)cos[(120 rad/s)t ]. Then
(b) I  C 
X C 1736 
SET UP:
31.13.
31.14.
31.15.
XC 
vR  iR  (4.38 103 A)(250 )cos((120 rad s)t )  (1.10 V)cos((120 rad s)t ).
EVALUATE: The voltage across the resistor has a different phase than the voltage across the capacitor.
IDENTIFY and SET UP: The voltage and current for a resistor are related by vR  iR. Deduce the frequency of the
voltage and use this in Eq.(31.12) to calculate the inductive reactance. Eq.(31.10) gives the voltage across the
inductor.
EXECUTE: (a) vR  (3.80 V)cos[(720 rad/s)t ]
v
 3.80 V 
vR  iR, so i  R  
 cos[(720 rad/s)t ]  (0.0253 A)cos[(720 rad/s)t ]
R  150  
(b) X L   L
  720 rad/s, L  0.250 H, so X L   L  (720 rad/s)(0.250 H)  180 
(c) If i  I cost then vL  VL cos(t  90) (from Eq.31.10). VL  I L  IX L  (0.02533 A)(180 )  4.56 V
vL  (4.56 V)cos[(720 rad/s)t  90]
But cos(a  90)  sin a (Appendix B), so vL  (4.56 V)sin[(720 rad/s)t ].
EVALUATE: The current is the same in the resistor and inductor and the voltages are 90 out of phase, with the
voltage across the inductor leading.
IDENTIFY: Calculate the reactance of the inductor and of the capacitor. Calculate the impedance and use that
result to calculate the current amplitude.
X
V
SET UP: With no capacitor, Z  R 2  X L2 and tan   L . X L   L. I  . VL  IX L and VR  IR. For an
R
Z
inductor, the voltage leads the current.
EXECUTE: (a) X L   L  (250 rad/s)(0.400 H)  100 . Z  (200 )2  (100 ) 2  224 .
V 30.0 V
(b) I  
 0.134 A
Z 224 
(c) VR  IR  (0.134 A)(200 )  26.8 V. VL  IX L  (0.134 A)(100 )  13.4 V.
X
100 
(d) tan   L 
and   26.6°. Since  is positive, the source voltage leads the current.
R 200 
(e) The phasor diagram is sketched in Figure 31.14.
EVALUATE: Note that VR  VL is greater than V. The loop rule is satisfied at each instance of time but the voltages
across R and L reach their maxima at different times.
Figure 31.14
IDENTIFY: vR (t ) is given by Eq.(31.8). vL (t ) is given by Eq.(31.10).
SET UP: From Exercise 31.14, V  30.0 V , VR  26.8 V , VL  13.4 V and   26.6° .
EXECUTE: (a) The graph is given in Figure 31.15.
(b) The different voltages are v  (30.0 V)cos(250t  26.6), vR  (26.8 V)cos(250t ),
vL  (13.4 V)cos(250t  90). At t  20 ms: v  20.5 V, vR  7.60 V, vL  12.85 V. Note that vR  vL  v.
NAlternating Current
31-5
(c) At t  40 ms: v  15.2 V, vR  22.49 V, vL  7.29 V. Note that vR  vL  v.
EVALUATE: It is important to be careful with radians versus degrees in above expressions!
31.16.
Figure 31.15
IDENTIFY: Calculate the reactance of the inductor and of the capacitor. Calculate the impedance and use that
result to calculate the current amplitude.
X  XC
1
SET UP: With no resistor, Z  ( X L  X C ) 2  X L  X C . tan   L
. XC 
. X L   L. For an
zero
C
inductor, the voltage leads the current. For a capacitor, the voltage lags the current.
1
1

 667 .
EXECUTE: (a) X L   L  (250 rad/s)(0.400 H)  100 . X C 
 C (250 rad/s)(6.00  106 F)
Z  X L  X C  100   667   567 .
V 30.0 V

 0.0529 A
Z 567 
(c) VC  IX C  (0.0529 A)(667 )  35.3 V. VL  IX L  (0.0529 A)(100 )  5.29 V.
X  X C 100   667 
(d) tan   L

  and   90°. The phase angle is negative and the source voltage lags
zero
zero
the current.
(e) The phasor diagram is sketched in Figure 31.16.
EVALUATE: When X C  X L the phase angle is negative and the source voltage lags the current.
(b) I 
Figure 31.16
31.17.
IDENTIFY and SET UP: Calculate the impendance of the circuit and use Eq.(31.22) to find the current amplitude.
The voltage amplitudes across each circuit element are given by Eqs.(31.7), (31.13), and (31.19). The phase angle
is calculated using Eq.(31.24). The circuit is shown in Figure 31.17a.
No inductor means X L  0
R  200 , C  6.00 106 F,
V  30.0 V,   250 rad/s
Figure 31.17a
31-6
Chapter 31
EXECUTE: (a) X C 
1
1

 666.7 
 C (250 rad/s)(6.00 106 F)
Z  R 2  ( X L  X C ) 2  (200 ) 2  (666.7 ) 2  696 
V 30.0 V

 0.0431 A  43.1 mA
Z 696 
(c) Voltage amplitude across the resistor: VR  IR  (0.0431 A)(200 )  8.62 V
Voltage amplitude across the capacitor: VC  IX C  (0.0431 A)(666.7 )  28.7 V
X  X C 0  666.7 
(d) tan   L

 3.333 so   73.3
R
200 
The phase angle is negative, so the source voltage lags behind the current.
(e) The phasor diagram is sketched qualitatively in Figure 31.17b.
(b) I 
31.18.
31.19.
Figure 31.17b
EVALUATE: The voltage across the resistor is in phase with the current and the capacitor voltage lags the current
by 90. The presence of the capacitor causes the source voltage to lag behind the current. Note that VR  VC  V .
The instantaneous voltages in the circuit obey the loop rule at all times but because of the phase differences the
voltage amplitudes do not.
IDENTIFY: vR (t ) is given by Eq.(31.8). vC (t ) is given by Eq.(31.16).
SET UP: From Exercise 31.17, V  30.0 V, VR  8.62 V, VC  28.7 V and   73.3°.
EXECUTE: (a) The graph is given in Figure 31.18.
(b) The different voltage are:
v  (30.0 V)cos(250t  73.3), vR  (8.62 V)cos(250t ), vC  (28.7 V)cos(250t  90). At t  20 ms :
v  25.1 V, vR  2.45 V, vC  27.5 V. Note that vR  vC  v.
(c) At t  40 ms: v  22.9 V, vR  7.23 V, vC  15.6 V. Note that vR  vC  v.
EVALUATE: It is important to be careful with radians vs. degrees!
Figure 31.18
IDENTIFY: Apply the equations in Section 31.3.
SET UP:   250 rad/s, R  200 , L  0.400 H, C  6.00 F and V  30.0 V.
EXECUTE: (a) Z  R2  ( L  1/ C )2 .
Z  (200 )2  ((250 rad/s)(0.0400 H) 1/((250 rad/s)(6.00 106 F)))2  601 
V
30 V
 0.0499 A.
(b) I  
Z 601 
 100   667  
  L  1/  C 
(c)   arctan 
  70.6, and the voltage lags the current.
  arctan 
R
200 




NAlternating Current
31-7
(d) VR  IR  (0.0499 A)(200 )  9.98 V;
VL  I L  (0.0499 A)(250 rad s)(0.400 H)  4.99 V; VC 
I
(0.0499 A)

 33.3 V.
 C (250 rad/s)(6.00  106 F)
EVALUATE: (e) At any instant, v  vR  vC  vL . But vC and v L are 180° out of phase, so vC can be larger than v
at a value of t, if vL  vR is negative at that t.
31.20.
IDENTIFY:
vR (t ) is given by Eq.(31.8). vC (t ) is given by Eq.(31.16). vL (t ) is given by Eq.(31.10).
SET UP: From Exercise 31.19, V  30.0 V, VL  4.99 V, VR  9.98 V, VC  33.3 V and   70.6°.
EXECUTE: (a) The graph is sketched in Figure 31.20. The different voltages plotted in the graph are:
v  (30 V)cos(250t  70.6), vR  (9.98 V)cos(250t ), vL  (4.99 V)cos(250t  90) and vC  (33.3 V)cos(250t  90).
(b) At t  20 ms: v  24.3 V, vR  2.83 V, vL  4.79 V, vC   31.9 V.
(c) At t  40 ms: v  23.8 V, vR  8.37 V, vL  2.71 V, vC  18.1 V.
EVALUATE: In both parts (b) and (c), note that the source voltage equals the sum of the other voltages at the
given instant. Be careful with degrees versus radians!
Figure 31.20
31.21.
IDENTIFY and SET UP: The current is largest at the resonance frequency. At resonance, X L  X C and Z  R. For
part (b), calculate Z and use I  V / Z .
1
EXECUTE: (a) f 0 
 113 Hz. I  V / R  15.0 mA.
2 LC
(b) X C  1/ C  500 . X L   L  160 . Z  R 2  ( X L  X C ) 2  (200 ) 2  (160   500 ) 2  394.5 .
I  V / Z  7.61mA. X C  X L so the source voltage lags the current.
31.22.
EVALUATE: 0  2 f0  710 rad/s.   400 rad/s and is less than  0 . When    0 , X C  X L . Note that I in
part (b) is less than I in part (a).
IDENTIFY: The impedance and individual reactances depend on the angular frequency at which the circuit is
driven.
2
1 

SET UP: The impedance is Z  R 2    L 
 , the current amplitude is I = V/Z, and the instantaneous

C

values of the potential and current are v = V cos(t + ), where tan  = (XL – XC)/R, and i = I cos t.
1
1
1
EXECUTE: (a) Z is a minimum when  L 
, which gives  
= 3162 rad/s =

C
LC
(8.00 mH)(12.5 µF)
3160 rad/s and Z = R = 175 Ω.
(b) I = V/Z = (25.0 V)/(175 Ω) = 0.143 A
(c) i = I cos t = I/2, so cost =
1
2
,
which gives t = 60° = π/3 rad. v = V cos(t + ), where tan  = (XL – XC)/R =
0/R =0. So, v = (25.0 V) cost = (25.0 V)(1/2) = 12.5 V.
vR = Ri = (175 Ω)(1/2)(0.143 A) = 12.5 V.
0.143 A
cos(60  90) = +3.13 V.
vC = VC cos(t – 90°) = IXC cos(t – 90°) =
(3162 rad/s)(12.5 µF)
31-8
Chapter 31
31.23.
vL = VL cos(t + 90°) = IXL cos(t + 90°) = (0.143 A)(3162 rad/s)(8.00 mH) cos(60° + 90°).
vL = –3.13 V.
(d) vR + vL + vC = 12.5 V + (–3.13 V) + 3.13 V = 12.5 V = vsource
EVALUATE: The instantaneous potential differences across all the circuit elements always add up to the value of
the source voltage at that instant. In this case (resonance), the potentials across the inductor and capacitor have the
same magnitude but are 180° out of phase, so they add to zero, leaving all the potential difference across the
resistor.
IDENTIFY and SET UP: Use the equation that preceeds Eq.(31.20): V 2  VR2  (VL  VC )2
31.24.
EXECUTE: V  (30.0 V)2  (50.0 V  90.0 V) 2  50.0 V
EVALUATE: The equation follows directly from the phasor diagrams of Fig.31.13 (b or c). Note that the voltage
amplitudes do not simply add to give 170.0 V for the source voltage.
1
IDENTIFY and SET UP: X L   L and X C 
.
C
1
L
1
1
EXECUTE: (a) If   0 
, then X   L 
and X 

 0.
C
LC
LC C LC
(b) When   0 , X  0
(c) When   0 , X  0
(d) The graph of X versus  is given in Figure 31.24.
EVALUATE:
Z  R 2  X 2 and tan   X / R.
Figure 31.24
31.25.
2
R.
IDENTIFY: For a pure resistance, Pav  Vrms I rms  I rms
SET UP: 20.0 W is the average power Pav .
EXECUTE: (a) The average power is one-half the maximum power, so the maximum instantaneous power is
40.0 W.
P
20.0 W
 0.167 A
(b) I rms  av 
Vrms 120 V
P
20.0 W
 720 
(c) R  2av 
I rms (0.167 A) 2
31.26.
VR2,rms
2
Vrms
(120 V) 2

 20.0 W.
R
R
750 
IDENTIFY: The average power supplied by the source is P  Vrms I rms cos . The power consumed in the resistance
EVALUATE: We can also calculate the average power as Pav 

2
R.
is P  I rms
SET UP:
  2 f  2 (1.25  103 Hz)  7.854  103 rad/s. X L   L  157 . X C 
1
C
 909 .
EXECUTE: (a) First, let us find the phase angle between the voltage and the current:
X  X C 157   909 
tan   L

and   65.04. The impedance of the circuit is
R
350 
Z  R 2  ( X L  X C ) 2  (350 ) 2  (752 ) 2  830 . The average power provided by the generator is then
P  Vrms I rms cos( ) 
2
Vrms
(120 V)2
cos( ) 
cos(65.04)  7.32 W
Z
830 
NAlternating Current
31-9
2
31.27.
 120 V 
2
(b) The average power dissipated by the resistor is PR  I rms
R
 (350 )  7.32 W.
 830  
EVALUATE: Conservation of energy requires that the answers to parts (a) and (b) are equal.
IDENTIFY: The power factor is cos , where  is the phase angle in Fig.31.13. The average power is given by
Eq.(31.31). Use the result of part (a) to rewrite this expression.
(a) SET UP: The phasor diagram is sketched in Figure 31.27.
EXECUTE:
From the diagram
V
IR R
cos  R 
 ,
V IZ Z
as was to be shown.
31.28.
31.29.
Figure 31.27
V
 R  V 
2
(b) Pav  Vrms I rms cos   Vrms I rms     rms  I rms R. But rms  I rms , so Pav  I rms
R.
Z
Z  Z 
EVALUATE: In an L-R-C circuit, electrical energy is stored and released in the inductor and capacitor but none is
dissipated in either of these circuit elements. The power delivered by the source equals the power dissipated in the
resistor.
V
R
IDENTIFY and SET UP: Pav  Vrms I rms cos . I rms  rms . cos  .
Z
Z
80.0 V
75.0 
EXECUTE: I rms 
 0.762 A. cos 
 0.714. Pav  (80.0 V)(0.762 A)(0.714)  43.5 W.
105 
105 
EVALUATE: Since the average power consumed by the inductor and by the capacitor is zero, we can also
2
R  (0.762 A) 2 (75.0 )  43.5 W.
calculate the average power as Pav  I rms
IDENTIFY and SET UP: Use the equations of Section 31.3 to calculate  , Z and Vrms . The average power
2
R
delivered by the source is given by Eq.(31.31) and the average power dissipated in the resistor is I rms
EXECUTE: (a) X L   L  2 f L  2 (400 Hz)(0.120 H)  301.6 
1
1
1
XC 


 54.51 
 C 2 fC 2 (400 Hz)(7.3 106 Hz)
X  X C 301.6   54.41 
tan   L

, so   45.8. The power factor is cos  0.697.
R
240 
(b) Z  R 2  ( X L  X C ) 2  (240 ) 2  (301.6   54.51 ) 2  344 
(c) Vrms  I rms Z  (0.450 A)(344 )  155 V
(d) Pav  I rmsVrms cos  (0.450 A)(155 V)(0.697)  48.6 W
31.30.
2
R  (0.450 A)2 (240 )  48.6 W
(e) Pav  I rms
EVALUATE: The average electrical power delivered by the source equals the average electrical power consumed
in the resistor.
(f ) All the energy stored in the capacitor during one cycle of the current is released back to the circuit in another
part of the cycle. There is no net dissipation of energy in the capacitor.
(g) The answer is the same as for the capacitor. Energy is repeatedly being stored and released in the inductor, but
no net energy is dissipated there.
IDENTIFY: The angular frequency and the capacitance can be used to calculate the reactance X C of the
capacitor. The angular frequency and the inductance can be used to calculate the reactance X L of the inductor.
Calculate the phase angle  and then the power factor is cos. Calculate the impedance of the circuit and then the
rms current in the circuit. The average power is Pav  Vrms I rms cos . On the average no power is consumed in the
capacitor or the inductor, it is all consumed in the resistor.
V
45 V
SET UP: The source has rms voltage Vrms 

 31.8 V.
2
2
31-10
Chapter 31
EXECUTE:
X L   L  (360 rad/s)(15 103 H)  5.4 . X C 
1
1

 794 .
 C (360 rad/s)(3.5  106 F)
X L  X C 5.4   794 
and   72.4°. The power factor is cos  0.302.

R
250 
V
31.8 V
(b) Z  R 2  ( X L  X C ) 2  (250 ) 2  (5.4   794 ) 2  827 . I rms  rms 
 0.0385 A.
Z
827 
Pav  Vrms I rms cos  (31.8 V)(0.0385 A)(0.302)  0.370 W.
tan  
31.31.
2
R  (0.0385 A) 2 (250 )  0.370 W. The average power
(c) The average power delivered to the resistor is Pav  I rms
delivered to the capacitor and to the inductor is zero.
EVALUATE: On average the power delivered to the circuit equals the power consumed in the resistor. The
capacitor and inductor store electrical energy during part of the current oscillation but each return the energy to the
circuit during another part of the current cycle.
IDENTIFY and SET UP: At the resonance frequency, Z = R. Use that V = IZ, VR  IR, VL  IX L and VC  IX C . Pav
is given by Eq.(31.31).
(a) EXECUTE: V  IZ  IR  (0.500 A)(300 )  150 V
(b) VR  IR  150 V
X L   L  L(1/ LC )  L / C  2582 ; VL  IX L  1290 V
X C  1/(C)  L / C  2582 ; VC  IX C  1290 V
(c) Pav  12 VI cos   12 I 2 R, since V  IR and cos   1 at resonance.
Pav  12 (0.500 A) 2 (300 )  37.5 W
EVALUATE: At resonance VL  VC . Note that VL  VC  V . However, at any instant vL  vC  0.
31.32.
31.33.
IDENTIFY: The current is maximum at the resonance frequency, so choose C such that   50.0 rad/s is the
resonance frequency. At the resonance frequency Z  R.
SET UP: VL  I L
V
EXECUTE: (a) The amplitude of the current is given by I 
. Thus, the current will have a
2
R  ( L  1 ) 2
C
1
1
1
. Therefore, C  2 
maximum amplitude when  L 
 44.4  F.
C
 L (50.0 rad/s) 2 (9.00 H)
(b) With the capacitance calculated above we find that Z  R, and the amplitude of the current is
120 V
I V 
 0.300 A. Thus, the amplitude of the voltage across the inductor is
R 400 
VL  I ( L)  (0.300 A)(50.0 rad/s)(9.00 H)  135 V.
EVALUATE: Note that VL is greater than the source voltage amplitude.
IDENTIFY and SET UP: At resonance X L  X C ,   0 and Z  R. R  150 , L  0.750 H,
C  0.0180  F, V  150 V
EXECUTE: (a) At the resonance frequency X L  X C and from tan  
power factor is cos  1.00.
(b) Pav  12 VI cos (Eq.31.31)
At the resonance frequency Z = R, so I 
31.34.
X L  XC
we have that   0 and the
R
V V

Z R
V 2 1 (150 V)2
V 
Pav  12 V   cos  12
2
 75.0 W
R
150 
 R
(c) EVALUATE: When C and f are changed but the circuit is kept on resonance, nothing changes in
Pav  V 2 /(2 R), so the average power is unchanged: Pav  75.0 W. The resonance frequency changes but since Z =
R at resonance the current doesn’t change.
1
IDENTIFY:  0 
. VC  IX C . V  IZ .
LC
SET UP: At resonance, Z  R.
NAlternating Current
EXECUTE: (a) 0 
31.35.
31-11
1
1

 1.54 104 rad/s
LC
(0.350 H)(0.0120 106 F)
V 
V 
1
1

 5.41  103 .
(b) V  IZ   C  Z   C  R. X C 
4
 C (1.54  10 rad/s)(0.0120  106 F)
 XC 
 XC 
 550 V 
V 
 (400 )  40.7 V.
3
 5.4110  
EVALUATE: The voltage amplitude for the capacitor is more than a factor of 10 times greater than the voltage
amplitude of the source.
1
1
IDENTIFY and SET UP: The resonance angular frequency is  0 
and
. X L   L. X C 
C
LC
Z  R 2  ( X L  X C ) 2 . At the resonance frequency X L  X C and Z  R.
EXECUTE: (a) Z  R  115 
1
(b) 0 
 1.33 104 rad/s .   2 0  2.66  104 rad/s.
3
6
(4.50 10 H)(1.26 10 F)
X L   L  (2.66  104 rad/s)(4.50  103 H)  120 . X C 
1
1

 30 
4
 C (2.66 10 rad/s)(1.25  106 F)
Z  (115 )2  (120   30 ) 2  146 
(c)   0 / 2  6.65  103 rad/s. X L  30 . X C 
31.36.
1
C
 120 . Z  (115 )2  (30   120 )2  146 , the
same value as in part (b).
EVALUATE: For   20 , X L  X C . For   0 / 2, X L  X C . But ( X L  X C ) 2 has the same value at these two
frequencies, so Z is the same.
IDENTIFY: At resonance Z  R and X L  X C .
1
. V  IZ . VR  IR, VL  IX L and VC  VL .
LC
1
1

 945 rad s.
EXECUTE: (a)  0 
LC
 0.280 H   4.00  106 F
SET UP:
0 
(b) I = 1.20 A at resonance, so R  Z 
V 120 V

 70.6 
I 1.70 A
(c) At resonance, VR  120 V, VL  VC  I L  1.70 A  945 rad s  0.280 H   450 V.
31.37.
EVALUATE: At resonance, VR  V and VL  VC  0.
IDENTIFY and SET UP: Eq.(31.35) relates the primary and secondary voltages to the number of turns in each. I =
2
2
 Vrms
/ R.
V/R and the power consumed in the resistive load is I rms
EXECUTE: (a)
V2 N 2
N
V 120 V

so 1  1 
 10
V1 N1
N 2 V2 12.0 V
V2 12.0 V

 2.40 A
R 5.00 
(c) Pav  I 22 R  (2.40 A) 2 (5.00 )  28.8 W
(d) The power drawn from the line by the transformer is the 28.8 W that is delivered by the load.
(b) I 2 
Pav 
2
V2
V 2 (120 V)2
so R 

 500 
R
Pav 28.8 W
N 
And  1  (5.00 )  (10) 2 (5.00 )  500 , as was to be shown.
 N2 
EVALUATE: The resistance is “transformed”. A load of resistance R connected to the secondary draws the same
power as a resistance ( N1 / N 2 ) 2 R connected directly to the supply line, without using the transformer.
31-12
Chapter 31
31.38.
IDENTIFY:
SET UP:
Pav  VI and Pav,1  Pav,2 .
V1  120 V. V2  13,000 V.
EXECUTE: (a)
31.39.
N1 V1
 .
N 2 V2
N 2 V2 13,000 V
 
 108
N1 V1
120 V
(b) Pav  V2 I 2  (13,000 V)(8.50 103 A)  110 W
P
110 W
 0.917 A
(c) I1  av 
V1 120 V
EVALUATE: Since the power supplied to the primary must equal the power delivered by the secondary, in a stepup transformer the current in the primary is greater than the current in the secondary.
V
N
IDENTIFY: A transformer transforms voltages according to 2  2 . The effective resistance of a secondary
V1 N1
R
V2
. Resistance R is related to Pav and V by Pav 
circuit of resistance R is Reff 
. Conservation of energy
2
( N 2 / N1 )
R
requires Pav,1  Pav,2 so V1I1  V2 I 2 .
SET UP: Let V1  240 V and V2  120 V, so P2,av  1600 W. These voltages are rms.
31.40.
EXECUTE: (a) V1  240 V and we want V2  120 V, so use a step-down transformer with N2 / N1  12 .
P 1600 W
(b) Pav  VI , so I  av 
 6.67 A.
V
240 V
V 2 (120 V)2
(c) The resistance R of the blower is R 

 9.00 . The effective resistance of the blower is
P 1600 W
9.00 
Reff 
 36.0 .
(1/ 2) 2
EVALUATE: I 2V2  (13.3 A)(120 V)  1600 W. Energy is provided to the primary at the same rate that it is
consumed in the secondary. Step-down transformers step up resistance and the current in the primary is less than
the current in the secondary.
1
IDENTIFY: Z  R 2  ( X L  X C ) 2 , with X L   L and X C 
.
C
SET UP: The woofer has a R and L in series and the tweeter has a R and C in series.
EXECUTE: (a) Z tweeter  R 2  (1 C )2
(b) Zwoofer  R2   L 
2
(c) If Z tweeter  Z woofer , then the current splits evenly through each branch.
(d) At the crossover point, where currents are equal, R 2  1  C 2   R 2   L  .  
2
f 
31.41.
31.42.

1

.
2 2 LC
1
and
LC
EVALUATE: The crossover frequency corresponds to the resonance frequency of a R-C-L circuit, since the
crossover frequency is where X L  X C .
IDENTIFY and SET UP: Use Eq.(31.24) to relate L and R to  . The voltage across the coil leads the current in it
by 52.3, so   52.3.
X  XC
X
EXECUTE: tan   L
. But there is no capacitance in the circuit so X C  0. Thus tan   L and X L 
R
R
XL
62.1 

 0.124 H.
R tan  (48.0 )tan52.3  62.1 . X L   L  2 f L so L 
2 f 2 (80.0 Hz)
EVALUATE:   45 when ( X L  X C )  R, which is the case here.
IDENTIFY:
SET UP:
Z  R 2  ( X L  X C ) 2 . I rms 
Vrms 
V
30.0 V

 21.2 V.
2
2
Vrms
. Vrms  I rms R. VC ,rms  I rms X C . VL ,rms  I rms X L .
Z
NAlternating Current
31-13
EXECUTE: (a)   200 rad/s , so X L   L  (200 rad/s)(0.400 H)  80.0  and
XC 
1
1

 833 . Z  (200 )2  (80.0   833 ) 2  779 .
 C (200 rad/s)(6.00  106 F)
I rms 
Vrms 21.2 V

 0.0272 A. V1 reads VR ,rms  I rms R  (0.0272 A)(200 )  5.44 V. V2 reads
Z
779 
 I rms X L  (0.0272 A)(80.0 )  2.18 V. V3 reads VC ,rms  I rms X C  (0.0272 A)(833 )  22.7 V. V4 reads
VL ,rms
VL  VC
 VL,rms  VC ,rms  2.18 V  22.7 V  20.5 V. V5 reads Vrms  21.2 V.
2
1
833 
(b)   1000 rad/s so X L   L  (5)(80.0 )  400  and X C 

 167 .
C
5
V
21.2 V
Z  (200 )2  (400   167 )2  307 . I rms  rms 
 0.0691 A. V1 reads VR ,rms  13.8 V. V2 reads
Z
307 
VL ,rms  27.6 V. V3 reads VC ,rms  11.5 V. V4 reads VL,rms  VC ,rms  27.6 V  11.5 V  16.1 V. V5 reads
Vrms  21.2 V.
1
 645 rad/s. 200 rad/s is less than the
LC
resonance frequency and X C  X L . 1000 rad/s is greater than the resonance frequency and X L  X C .
IDENTIFY and SET UP: The rectified current equals the absolute value of the current i. Evaluate the integral as
specified in the problem.
EXECUTE: (a) From Fig.31.3b, the rectified current is zero at the same values of t for which the sinusoidal
current is zero. At these t, cos  t  0 and  t   / 2, 3 / 2, . The two smallest positive times are
t1   / 2 , t2  3 / 2.
EVALUATE: The resonance frequency for this circuit is  0 
31.43.
(b) A 

t2
t1
t
2
t2
I
1

idt   I costdt   I  sin t    (sin t2  sin t1 )
t1


 t1
sin t1  sin[ ( / 2 )]  sin( / 2)  1
sin t2  sin[ (3 / 2 )]  sin(3 / 2)  1
2I
I 
A    (1  (1)) 

 
(c ) I rav (t2  t1 )  2I / 
I rav 
31.44.
2I
2I
(b) Z  R2  X L 2 
Vrms  Z
 400    250 
2
2
 472 . cos  
V
V2 R
R
and I rms  rms . Pav  rms , so
Z Z
Z
Z
Pav
800 W
  472  
 668 V.
R
400 
EVALUATE:
31.45.
2I

 , which is Eq.(31.3).
 (t2  t1 )  (3 / 2   / 2 ) 
EVALUATE: We have shown that Eq.(31.3) is correct. The average rectified current is less than the current
amplitude I, since the rectified current varies between 0 and I. The average of the current is zero, since it has both
positive and negative values.
IDENTIFY: X L   L. Pav  Vrms I rms cos
SET UP: f  120 Hz;   2 f .
X
250 
EXECUTE: (a) X L   L  L  L 
 0.332 
 2 120 Hz 
I rms 
Vrms 668 V
2
R  (1.415 A) 2 (400 )  800 W, which

 1.415 A. We can calculate Pav as I rms
Z
472 
checks.
(a) IDENTIFY and SET UP: Source voltage lags current so it must be that X C  X L and we must add an inductor
in series with the circuit. When X C  X L the power factor has its maximum value of unity, so calculate the
additional L needed to raise X L to equal X C .
31-14
Chapter 31
(b) EXECUTE: power factor cos equals 1 so   0 and X C  X L . Calculate the present value of X C  X L to
see how much more X L is needed: R  Z cos  (60.0 )(0.720)  43.2 
X L  XC
so X L  X C  R tan 
R
cos  0.720 gives   43.95 (  is negative since the voltage lags the current)
tan  
Then X L  X C  R tan   (43.2 ) tan(43.95)  41.64 .
Therefore need to add 41.64  of X L .
XL
41.64 

 0.133 H, amount of inductance to add.
2 f 2 (50.0 Hz)
EVALUATE: From the information given we can’t calculate the original value of L in the circuit, just how much
to add. When this L is added the current in the circuit will increase.
2
R
IDENTIFY: Use Vrms  I rms Z to calculate Z and then find R. Pav  I rms
X L   L  2 f L and L 
31.46.
SET UP:
X C  50.0 
EXECUTE:
R
Z
Vrms 240 V
2

 80.0   R 2  X C2  R 2   50.0   . Thus,
I rms 3.00 A
80.0   50.0 
2
2
 62.4 . The average power supplied to this circuit is equal to the power dissipated
2
by the resistor, which is P  I rms
R   3.00 A   62.4    562 W.
2
X L  X C 50.0 
and   38.7°.

R
62.4 
Pav  Vrms I rms cos  (240 V)(3.00 A)cos(38.7°)  562 W, which checks.
IDENTIFY: The voltage and current amplitudes are the maximum values of these quantities, not necessarily the
instantaneous values.
SET UP: The voltage amplitudes are VR = RI, VL = XLI, and VC = XCI, where I = V/Z and
EVALUATE:
31.47.
tan  
2
1 

Z  R2   L 
.
C 

EXECUTE: (a)  = 2πf = 2π(1250 Hz) = 7854 rad/s. Carrying extra figures in the calculator gives XL = L =
(7854 rad/s)(3.50 mH) = 27.5 Ω; XC = 1/C = 1/[(7854 rad/s)(10.0 µF)] = 12.7 Ω;
Z  R 2  ( X L  X C )2 =
(50.0 )2  (27.5  12.7 ) 2 = 52.1 Ω;
I = V/Z = (60.0 V)/(52.1 Ω) = 1.15 A; VR = RI = (50.0 Ω)(1.15 A) = 57.5 V;
VL = XLI = (27.5 Ω)(1.15 A) = 31.6 V; VC = XCI = (12.7 Ω)(1.15 A) = 14.7 V.
The voltage amplitudes can add to more than 60.0 V because these voltages do not all occur at the same instant of
time. At any instant, the instantaneous voltages all add to 60.0 V.
(b) All of them will change because they all depend on . XL = L will double to 55.0 Ω, and XC = 1/C will
31.48.
decrease by half to 6.35 Ω. Therefore Z  (50.0 )2  (55.0   6.35 ) 2 = 69.8 Ω; I = V/Z = (60.0 V)/(69.8 Ω) =
0.860 A; VR = IR = (0.860 A)(50.0 Ω) = 43.0 V;
VL = IXL = (0.860 A)(55.0 Ω) = 47.3 V; VC = IXC = (0.860 A)(6.35 Ω) = 5.47 V.
EVALUATE: The new amplitudes in part (b) are not simple multiples of the values in part (a) because the
impedance and reactances are not all the same simple multiple of the angular frequency.
1
IDENTIFY and SET UP: X C 
. X L   L.
C
1
XL
L
1
1
 1L and LC  2 . At angular frequency 2 ,
 2   22 LC  (21 ) 2 2  4.
EXECUTE: (a)
1C
1
X C 1/  2C
1
X L  XC.
XL
   1  1
 32 LC   1   2   . X C  X L .
XC
 3   1  9
When  increases, X L increases and X C decreases. When  decreases, X L decreases and X C
2
(b) At angular frequency 3 ,
EVALUATE:
increases.
(c) The resonance angular frequency 0 is the value of  for which X C  X L , so 0  1.
NAlternating Current
31.49.
31-15
IDENTIFY and SET UP: Express Z and I in terms of , L, C and R. The voltages across the resistor and the
inductor are 90 out of phase, so Vout  VR2  VL2 .
EXECUTE: The circuit is sketched in Figure 31.49.
X L   L, X C 
1
C
2
1 

Z  R2    L 

C 

V
Vs
I s
2
Z
1 

R2    L 

C 

Figure 31.49
Vout  I R 2  X L2  I R 2   2 L2  Vs
Vout

Vs
R 2   2 L2
1 

R2   L 

C 

2
R 2   2 L2
1 

R2   L 

C 

2
 small
2
1 
1

2
2 2
2
As  gets small, R 2    L 
  2 2 ,R  L  R
C 
C

Therefore
Vout
R2

  RC as  becomes small.
Vs
(1/  2C 2 )
 large
2
1 

2
2 2
2 2
2
2 2
2 2
As  gets large, R2    L 
  R  L  L , R  L  L
C 

Therefore,
31.50.
Vout
 2 L2

 1 as  becomes large.
Vs
 2 L2
EVALUATE: Vout / Vs  0 as  becomes small, so there is Vout only when the frequency  of Vs is large. If the
source voltage contains a number of frequency components, only the high frequency ones are passed by this filter.
IDENTIFY: V  VC  IX C . I  V / Z .
SET UP:
EXECUTE:
X L   L, X C 
Vout  VC 
1
C
.
I
V
1
 out 
.
2
C
Vs C R   L  1 C 2
If  is large:
Vout
1
1
1



.
2
2
Vs C R 2   L  1 C 
 LC  2
C  L 
If  is small:
Vout

Vs  C
1
1 C 
2

C
 1.
C
EVALUATE: When  is large, X C is small and X L is large so Z is large and the current is small. Both factors in
31.51.
VC  IX C are small. When  is small, X C is large and the voltage amplitude across the capacitor is much larger
than the voltage amplitudes across the resistor and the inductor.
IDENTIFY: I  V / Z and Pav  12 I 2 R.
Z  R 2  ( L  1/ C )2
V
V
EXECUTE: (a) I  
.
2
2
Z
R   L  1  C 
SET UP:
31-16
Chapter 31
2
1
1 V 
V 2R 2
(b) Pav  I 2 R    R  2
.
2
2
2Z
R   L  1 C 
(c) The average power and the current amplitude are both greatest when the denominator is smallest, which occurs
1
1
for  0 L 
, so  0 
.
 0C
LC
25 2
100 V   200   2

.
2
2
2
 200      2.00 H   1 [ (0.500 106 F)] 40 ,000 2   2 2  2 ,000 ,000 
2
(d) Pav 
The graph of Pav versus  is sketched in Figure 31.51.
EVALUATE: Note that as the angular frequency goes to zero, the power and current are zero, just as they are
when the angular frequency goes to infinity. This graph exhibits the same strongly peaked nature as the light
purple curve in Figure 31.19 in the textbook.
Figure 31.51
31.52.
IDENTIFY:
I
VL  I L and VC 
.
C
SET UP: Problem 31.51 shows that I 
EXECUTE: (a) VL  I L 
(b) VC 
V
R  ( L  1/[ C ]) 2
2
.
V L
V L

.
2
Z
R 2   L  1/[C ]
I
I
1


.
2
C CZ C R   L  1 [C ]2
(c) The graphs are given in Figure 31.52.
EVALUATE: (d) When the angular frequency is zero, the inductor has zero voltage while the capacitor has
voltage of 100 V (equal to the total source voltage). At very high frequencies, the capacitor voltage goes to zero,
1
while the inductor’s voltage goes to 100 V. At resonance, 0 
 1000 rad s, the two voltages are equal, and
LC
are a maximum, 1000 V.
Figure 31.52
NAlternating Current
31.53.
31-17
U B  12 Li 2 . U E  12 Cv 2 .
IDENTIFY:
SET UP: Let  x denote the average value of the quantity x. i 2   12 I 2 and vC2   12 VC2 . Problem 31.51 shows
that I 
V
R  ( L  1/[ C ])
2
2
. Problem 31.52 shows that VC 
V
 C R  ( L  1/[C ]) 2
2
.
2
 I  1 2
2
 12 L 
EXECUTE: (a) U B  12 Li 2  U B  12 L i 2  12 LI rms
  4 LI .
 2
2
1
V 
U E  12 CvC2  U E  C vC2  12 CVC2,rms  12 C  C   14 CVC2
2
 2
(b) Using Problem 31.51a
UB

1
1
V2
 LI 2  L 
4
4  R 2   L  1  C  2

2

LV 2
 
.
 4 R 2   L  1  C  2



2
1
1
V
V2
Using Problem (31.47b): U E  CVC 2  C

.
2
4
4  2C 2 R2   L  1 C 2
4 2C R2   L  1 C 




(c) The graphs of the magnetic and electric energies are given in Figure 31.53.
EVALUATE: (d) When the angular frequency is zero, the magnetic energy stored in the inductor is zero, while the
electric energy in the capacitor is U E  CV 2 4. As the frequency goes to infinity, the energy noted in both
inductor and capacitor go to zero. The energies equal each other at the resonant frequency where 0 
UB  UE 
1
and
LC
LV 2
.
4R2
Figure 31.53
31.54.
IDENTIFY: At any instant of time the same rules apply to the parallel ac circuit as to parallel dc circuit: the
voltages are the same and the currents add.
SET UP: For a resistor the current and voltage in phase. For an inductor the voltage leads the current by 90° and
for a capacitor the voltage lags the current by 90°.
EXECUTE: (a) The parallel L-R-C circuit must have equal potential drops over the capacitor, inductor and
resistor, so vR  vL  vC  v. Also, the sum of currents entering any junction must equal the current leaving the
junction. Therefore, the sum of the currents in the branches must equal the current through the
source: i  iR  iL  iC .
(b) iR  v is always in phase with the voltage. iL  v lags the voltage by 90, and iC  vC leads the voltage
L
R
by 90. The phase diagram is sketched in Figure 31.54.
(c) From the diagram, I  I R   I C  I L 
2
2
2
(d) From part (c):
I V
2
V 
V  
     V C 
 .
R

L
  
2
2
1
1 
1 
V

  C 
 . But I  , so
2
Z
R
L 
Z

2
1 
1 
  C 
.
2
R 
 L 
31-18
Chapter 31
EVALUATE:
For large , Z 
1
. The current in the capacitor branch is much larger than the current in the
C
other branches. For small , Z   L. The current in the inductive branch is much larger than the current in the
other branches.
Figure 31.54
31.55.
IDENTIFY: Apply the expression for I from problem 31.54 when 0  1/ LC .
2
1 
1 
  C 
2
R
 L 

1
1
V
  0C 
 I C  V  0C 
 I so I  I R and I is a minimum.
EXECUTE: (a) At resonance, 0 
0 L
0 L L
LC
SET UP:
From Problem 31.54, I  V
2
Vrms
V2
at resonance where R < Z so power is a maximum.
cos  
Z
R
(c) At    0 , I and V are in phase, so the phase angle is zero, which is the same as a series resonance.
(b) Pav 
EVALUATE: (d) The parallel circuit is sketched in Figure 31.55. At resonance, iC  iL and at any instant of time
these two currents are in opposite directions. Therefore, the net current between a and b is always zero.
(e) If the inductor and capacitor each have some resistance, and these resistances aren’t the same, then it is no
longer true that iC  iL  0 and the statement in part (d) isn’t valid.
Figure 31.55
31.56.
IDENTIFY: Refer to the results and the phasor diagram in Problem 31.54. The source voltage is applied across
each parallel branch.
SET UP: V  2Vrms  311 V
EXECUTE: (a) I R 
V 311 V

 0.778 A.
R 400 
(b) I C  V C   311 V  360 rad s   6.00  106 F   0.672 A.
I 
 0.672 A 
(c)   arctan  C   arctan 
  40.8.
I
 0.778 A 
 R
(d) I  I R2  IC2 
31.57.
 0.778 A   0.672 A 
2
2
 1.03 A.
(e) Leads since   0.
EVALUATE: The phasor diagram shows that the current in the capacitor always leads the source voltage.
IDENTIFY and SET UP: Refer to the results and the phasor diagram in Problem 31.54. The source voltage is
applied across each parallel branch.
V
V
EXECUTE: (a) I R  ; IC  V C; I L 
.
R
L
(b) The graph of each current versus  is given in Figure 31.57a.
(c)   0 : IC  0; I L  .   : IC  ; I L  0.
At low frequencies, the current is not changing much so the inductor’s back-emf doesn’t “resist.” This allows the
current to pass fairly freely. However, the current in the capacitor goes to zero because it tends to “fill up” over the
slow period, making it less effective at passing charge. At high frequency, the induced emf in the inductor resists
the violent changes and passes little current. The capacitor never gets a chance to fill up so passes charge freely.
NAlternating Current
(d)  
31-19
1
1

 1000 rad sec and f  159 Hz. The phasor diagram is sketched in
LC
(2.0 H)(0.50 106 F)
Figure 31.57b.
2
2
V 
V  
(e) I      V C 
 .
R

L

 
2
2
 100 V  

100 V
1
6
I 
   (100 V)(1000 s )(0.50 10 F) 
  0.50 A
1
(1000 s )(2.0 H) 
 200   
(f ) At resonance I L  I C  V C  (100 V)(1000 s 1 )(0.50 106 F)  0.0500 A and I R 
V 100 V

 0.50 A.
R 200 
EVALUATE: At resonance iC  iL  0 at all times and the current through the source equals the current through the
resistor.
Figure 31.57
31.58.
IDENTIFY: The average power depends on the phase angle .
2
1 

SET UP: The average power is Pav = VrmsIrmscos , and the impedance is Z  R 2    L 
.
C 

, so  = π/3 = 60°. tan  = (XL – XC)/R,
which gives tan 60° = (L – 1/C)/R. Using R = 75.0 Ω, L = 5.00 mH, and C = 2.50 µF and solving for  we get
 = 28760 rad/s = 28,800 rad/s.
(b) Z  R 2  ( X L  X C ) 2 , where XL = L = (28,760 rad/s)(5.00 mH) = 144 Ω and
EXECUTE:
(a) Pav = VrmsIrmscos  =
1
2
(VrmsIrms), which gives cos  =
1
2
XC = 1/C = 1/[(28,760 rad/s)(2.50 µF)] = 13.9 Ω, giving Z  (75 )2  (144   13.9 ) 2 = 150 Ω;
31.59.
I = V/Z = (15.0 V)/(150 Ω) = 0.100 A and Pav = 12 VI cos  = 12 (15.0 V)(0.100 A)(1/2) = 0.375 W.
EVALUATE: All this power is dissipated in the resistor because the average power delivered to the inductor and
capacitor is zero.
2
R from Exercise 31.27 to calculate
IDENTIFY: We know R, X C and  so Eq.(31.24) tells us X L . Use Pav  I rms
Then
calculate
Z
and
use
Eq.(31.26)
to
calculate
for
the
source.
I rms .
Vrms
SET UP: Source voltage lags current so   54.0. X C  350 , R  180 , Pav  140 W
X  XC
EXECUTE: (a) tan   L
R
X L  R tan   X C  (180 ) tan(54.0)  350   248   350   102 
2
R (Exercise 31.27). I rms 
(b) Pav  Vrms I rms cos   I rms
Pav
140 W

 0.882 A
R
180 
(c) Z  R 2  ( X L  X C ) 2  (180 ) 2  (102   350 ) 2  306 
Vrms  I rms Z  (0.882 A)(306 )  270 V.
EVALUATE: We could also use Eq.(31.31): Pav  Vrms I rms cos
Pav
140 W
Vrms 

 270 V, which agrees. The source voltage lags the current when
I rms cos  (0.882 A)cos(54.0)
X C  X L , and this agrees with what we found.
31-20
Chapter 31
31.60.
IDENTIFY and SET UP: Calculate Z and I  V / Z .
EXECUTE: (a) For   800 rad s:
Z  R2  ( L  1 C )2  (500 )2  ((800 rad/s)(2.0 H) 1 ((800 rad/s)(5.0 107 F)))2 . Z  1030 .
V 100 V
1
0.0971 A
I 
 0.0971 A. VR  IR  (0.0971 A)(500 )  48.6 V, VC 

 243 V
 C (800 rad s)(5.0 107 F)
Z 1030 
  L  1 (C ) 
and VL  IL  (0.0971 A)(800 rad s)(2.00 H)  155 V.   arctan 
  60.9. The graph of each
R


voltage versus time is given in Figure 31.60a.
(b) Repeating exactly the same calculations as above for   1000 rad/s:
Z  R  500 ;   0; I  0.200 A; VR  V  100 V; VC  VL  400 V. The graph of each voltage versus time is
given in Figure 31.60b.
(c) Repeating exactly the same calculations as part (a) for   1250 rad/s:
Z  R  1030 ;   60.9; I  0.0971 A; VR  48.6 V; VC  155 V; VL  243 V. The graph of each voltage
versus time is given in Figure 31.60c.
1
1
EVALUATE: The resonance frequency is 0 

 1000 rad/s. For    0 the phase
LC
(2.00 H)(0.500  F)
angle is negative and for    0 the phase angle is positive.
Figure 31.60
NAlternating Current
31.61.
31-21
IDENTIFY and SET UP: Eq.(31.19) allows us to calculate I and then Eq.(31.22) gives Z. Solve Eq.(31.21) for L.
V
360 V
 0.750 A
EXECUTE: (a) VC  IX C so I  C 
X C 480 
V
120 V

 160 
I 0.750 A
(c) Z 2  R 2  ( X L  X C ) 2
(b) V  IZ so Z 
X L  X C   Z 2  R 2 , so
X L  X C  Z 2  R 2  480  ± (160 )2  (80.0 )2  480  ± 139 
X L  619  or 341 
1
and X L   L. At resonance, X C  X L . As the frequency is lowered below the
C
resonance frequency X C increases and X L decreases. Therefore, for   0 , X L  X C . So for X L  341  the
XC 
(d) EVALUATE:
angular frequency is less than the resonance angular frequency.  is greater than 0 when X L  619 . But at
these two values of X L , the magnitude of X L  X C is the same so Z and I are the same. In one case ( X L  691 )
31.62.
the source voltage leads the current and in the other ( X L  341 ) the source voltage lags the current.
IDENTIFY and SET UP: The maximum possible current amplitude occurs at the resonance angular frequency
because the impedance is then smallest.
EXECUTE: (a) At the resonance angular frequency 0  1/ LC , the current is a maximum and Z = R, giving
Imax = V/R. At the required frequency, I = Imax/3. I = V/Z = Imax/3 = (V/R)/3, which means that Z = 3R. Squaring
gives R2 + (L – 1/C)2 = 9R2 . Solving for  gives  = 3.192  105 rad/s and  = 8.35  104 rad/s.
I
V
49.5 V

 0.132 A.
(b) V  2Vrms  2(35.0 V)  49.5 V. I  max 
3
3R 3(125 )
For   8.35 104 rad/s: R  125  and VR  IR  16.5 ; X L   L  125  and VL  16.5 V;
1
 479  and VC  63.2 V.
C
For   3.192 105 rad/s: R  125  and VR  IR  16.5 ; X L   L  479  and VL  63.2 V;
XC 
XC 
1
C
 125  and VC  16.5 V.
For the lower frequency, X C  X L and VC  VL . For the higher frequency, X L  X C and VL  VC .
EVALUATE:
31.63.
IDENTIFY and SET UP: Consider the cycle of the repeating current that lies between t1   / 2 and t2  3 / 2. In
this interval i 
2I 0

(t   ). I av 
t2
t2
1
1
2
i dt and I rms

i 2dt


t2  t1 t1
t2  t1 t1
3 / 2
I av 
EXECUTE:
t2
1
1 3 / 2 2 I 0
2I  1

i dt  
(t   ) dt  20  t 2   t 

t

/
2
1
t2  t1


 2
 /2
2
3 2  2  2 
I
 2 I   9
I av   20  

    (2 I 0 ) 18 (9  12  1  4)  0 (13  13)  0.

8
2
8
2
4



2
I rms
 ( I 2 )av 
2
I rms

4 I 02

3
t2
1
1 3 / 2 4I 02
i 2dt  
(t   )2 dt

t
t2  t1 1
  /2  2
3 / 2

/2
(t   ) 2dt 
4 I 02      
3 3 / 2
1


(
t


)

 / 2 3 3  2     2 
 3 3

  
4 I 02
3
3



I 02
[1  1]  13 I 02
6
I
2
I rms  I rms
 0 .
3
EVALUATE: In each cycle the current has as much negative value as positive value and its average is zero. i 2 is
always positive and its average is not zero. The relation between I rms and the current amplitude for this current is
different from that for a sinusoidal current (Eq.31.4).
2
I rms

31-22
Chapter 31
31.64.
IDENTIFY: Apply Vrms  I rms Z
1
and Z  R 2  ( X L  X C ) 2 .
LC
1
1

 786 rad s.
EXECUTE: (a) 0 
LC
(1.80 H)(9.00 107 F)
0 
SET UP:
(b) Z  R 2  (L  1 C )2 . Z  (300 )2  ((786 rad s)(1.80 H)  1 ((786 rad s)(9.00 107 F)))2  300 .
I rms-0 
Vrms 60 V

 0.200 A.
Z
300 
(c) We want I 
 2 L2 
1
V
I rms-0  rms 
2
Z
Vrms
R  ( L  1 C )
2
2
. R 2  ( L 1 C )2 
2
4Vrms
.
2
I rms-0
2

 1
2 L 4Vrms
1
2L
4V 2
 2   2  0.

 R 2  2 rms  0 and ( 2 ) 2 L2   2  R 2 
2
C
I
C
C
C
I rms-0
rms-0 

2
Substituting in the values for this problem, the equation becomes ( 2 )2 (3.24)   2 (4.27  106 )  1.23  1012  0.
Solving this quadratic equation in  2 we find  2  8.90 105 rad 2 s 2 or 4.28 105 rad 2 /s 2 and
  943 rad s or 654 rad s.
(d) (i) R  300 , I rms-0  0.200 A, 1  2  289 rad s. (ii) R  30 , I rms-0  2A, 1   2  28 rad/s.
(iii) R  3 , I rms-0  20 A, 1  2  2.88 rad/s.
31.65.
EVALUATE: The width gets smaller as R gets smaller; I rms-0 gets larger as R gets smaller.
IDENTIFY: The resonance frequency, the reactances, and the impedance all depend on the values of the circuit
elements.
SET UP: The resonance frequency is 0  1/ LC , the reactances are XL = L and XC = 1/C, and the impedance
is Z  R 2  ( X L  X C ) 2 .
1
 1/ 2, so 0 decreases by 12 .
2 L 2C
(b) Since XL = L, if L is doubled, XL increases by a factor of 2.
(c) Since XC = 1/C, doubling C decreases XC by a factor of 12 .
EXECUTE: (a) 0  1/ LC becomes
(d) Z  R 2  ( X L  X C ) 2  Z  (2 R) 2  (2 X L  12 X C ) 2 , so Z does not change by a simple factor of 2 or
31.66.
1
2
.
EVALUATE: The impedance does not change by a simple factor, even though the other quantities do.
V
N
IDENTIFY: A transformer transforms voltages according to 2  2 . The effective resistance of a secondary
V1 N1
R
.
circuit of resistance R is Reff 
( N 2 / N1 ) 2
SET UP: N 2  275 and V1  25.0 V.
EXECUTE: (a) V2  V1 ( N2 / N1 )  (25.0 V)(834/ 275)  75.8 V
R
125 

 13.6 
( N 2 / N1 ) 2 (834 / 275) 2
EVALUATE: The voltage across the secondary is greater than the voltage across the primary since N 2  N1. The
effective load resistance of the secondary is less than the resistance R connected across the secondary.
1
1
IDENTIFY: The resonance angular frequency is  0 
and the resonance frequency is f 0 
.
LC
2 LC
SET UP: 0 is independent of R.
(b) Reff 
31.67.
EXECUTE: (a) 0 (or f 0 ) depends only on L and C so change these quantities.
31.68.
(b) To double 0 , decrease L and C by multiplying each of them by 12 .
EVALUATE: Increasing L and C decreases the resonance frequency; decreasing L and C increases the resonance
frequency.
IDENTIFY: At resonance, Z  R. I  V / R. VR  IR, VC  IX C and VL  IX L . U E  12 CVC2 and U L  12 LI 2 .
SET UP: The amplitudes of each time dependent quantity correspond to the maximum values of those quantities.
NAlternating Current
EXECUTE: (a) I 
(c) VL  IX L 
31.69.
R0C

V L
.
R C
V
V L
0 L 
.
R
R C
1
1 V2 L 1 V2
(d) U C  CVC2  C 2  L 2 .
2
2 R C 2 R
1
1 V2
(e) U L  LI 2  L 2 .
2
2 R
EVALUATE: At resonance VC  VL and the maximum energy stored in the inductor equals the maximum energy
stored in the capacitor.
IDENTIFY: I  V / R. VR  IR, VC  IX C and VL  IX L . U E  12 CVC2 and U L  12 LI 2 .
SET UP: The amplitudes of each time dependent quantity correspond to the maximum values of those quantities.
EXECUTE:
(a) I 
V

Z

0
2
.
V
 L

R 2   0  2 / 0C 
2


(b) VC  IX C 
2
 0C
0 L
V
R2 
9 L
4C

2

V
.
9 L
R 
4C
2
L
C
2V
R2 
9 L
4C
V
.
L
V 2

.
C
9
L
9 L
2
2
R 
R 
4C
4C
1
2 LV 2
2
.
(d) U C  CVC 
9 L
2
R2 
4C
1 2 1 LV 2
.
(e) U L  LI 
2
2 R2  9 L
4C
EVALUATE: For    0 , VC  VL and the maximum energy stored in the capacitor is greater than the maximum
energy stored in the inductor.
IDENTIFY: I  V / R . VR  IR , VC  IX C and VL  IX L . U E  12 CVC2 and U L  12 LI 2 .
SET UP: The amplitudes of each time dependent quantity correspond to the maximum values of those quantities.
EXECUTE:   20 .
V
V
V
(a) I  

.
2
2
Z
9 L
R  (20 L  1/ 20C )
2
R 
4C
1
V
L
V 2

.
(b) VC  IX C 
2 0C
C
9 L
9 L
R2 
R2 
4C
4C
(c) VL  IX L 
31.70.
V
V
V
1
and I max  .

. At resonance  L 
2
2
Z

C
R
R   L  1/ C 
V
(b) VC  IX C 
31-23
2
(c) VL  IX L  2 0 L
V
9 L
R2 
4C
2
1
LV
(d) U C  CVC2 
.
2
9 L
2
8 R 
4C

L
C
2V
9 L
R 
4C
2
.
31-24
Chapter 31
31.71.
LV 2
.
9 L
2 R2 
4C
EVALUATE: For   0 , VL  VC and the maximum energy stored in the inductor is greater than the maximum
energy stored in the capacitor.
IDENTIFY and SET UP: Assume the angular frequency  of the source and the resistance R of the resistor are
known.
V
I L  L

EXECUTE: Connect the source, capacitor, resistor, and inductor in series. Measure VR and VL . L 
VR
IR
R
and L can be calculated.
EVALUATE: There are a number of other approaches. The frequency could be varied until VC  VL , and then this
31.72.
frequency is equal to 1/ LC . If C is known, then L can be calculated.
V
IDENTIFY: Pav  Vrms I rms cos and I rms  rms . Calculate Z. R  Z cos.
Z
SET UP: f  50.0 Hz and   2 f . The power factor is cos.
1
(e) U L  LI 2 
2
2
Vrms
V 2 cos (120 V)2 (0.560)
cos . Z  rms

 36.7 .
Z
Pav
(220 W)
R  Z cos  (36.7 )(0.560)  20.6 .
EXECUTE: (a) Pav 
(b) Z  R 2  X L 2  X L  Z 2  R 2  (36.7 )2  (20.6 ) 2  30.4 . But   0 is at resonance, so the inductive
and capacitive reactances equal each other. Therefore we need to add X C  30.4 . X C 
C
1
X C

31.73.
IDENTIFY:
SET UP:
therefore gives
1
1

 1.05 104 F.
2 f X C 2 (50.0 Hz)(30.4 )
(c) At resonance, Pav 
EVALUATE:
resonance.
1
C
V 2 (120 V)2

 699 W.
R
20.6 
2
Pav  I rms
R and I rms is maximum at resonance, so the power drawn from the line is maximum at
pR  i 2 R. pL  iL
i  I cost
di
q
. pC  i.
dt
C
1
EXECUTE: (a) pR  i 2 R  I 2 cos2 (t ) R  VR I cos 2 (t )  VR I (1  cos(2t )).
2
1 T
VR I T
VR I T 1
Pav ( R)   pR dt 
(1  cos(2t ))dt 
[t ]0  2 VR I .
T 0
2T 0
2T
T
di
(b) pL  Li   LI 2 cos(t )sin(t )   12 VL I sin(2t ). But  sin(2t )dt  0  Pav ( L)  0.
0
dt
T
q
(c) pC  i  vCi  VC I sin(t )cos(t )  12 VC I sin(2t ). But  sin(2t )dt  0  Pav (C )  0.
0
C
(d) p  pR  pL  pc  VR I cos 2 (t )  12 VL I sin(2t )  12 VC I sin(2t ) and
V V
VR
and sin   L C , so
V
V
p  VI cos(t )(cos cos(t )  sin sin(t )), at any instant of time.
EVALUATE: At an instant of time the energy stored in the capacitor and inductor can be changing, but there is no
net consumption of electrical energy in these components.
dVL
dVC
IDENTIFY: VL  IX L .
 0 at the  where VL is a maximum. VC  IX C .
 0 at the  where VC is a
d
d
maximum.
V
.
SET UP: Problem 31.51 shows that I 
2
R  ( L  1/  C ) 2
p  I cos(t )(VR cos(t )  VL sin(t )  VC sin(t )). But cos 
31.74.
EXECUTE: (a) VR maximum when VC  VL    0 
1
.
LC
NAlternating Current
31-25

dVL
d 
V L
dVL

.
0
 0.Therefore:
d
d  R 2  ( L  1 C )2 
d


VL
V  2 L( L  1  2C )( L  1  2C ) 2
2
0

. R  ( L  1  C )   2 ( L2  1  4C 2 ) .
2
2 3 2
2
2
(
R

(

L

1

C
)
)
R ( L  1 C )
(b) VL  maximum when
R2 
1
R 2C 2
1
2L
1
and  

LC




.
2
 2C 2 C
 2C 2  2
1
LC  R 2C 2 2
.

dVC
d 
V
dVC

.
0
 0. Therefore:
d
d
d  C R 2  ( L  1 C )2 


V
V ( L  1  2C )( L  1  2C ) 2
2
2
2
4 2
0

. R  ( L  1  C )   ( L  1  C ).
2
2 3 2
 2C R 2  ( L  1 C )2 C ( R  ( L  1 C ) )
(c) VC  maximum when
1
R2
2L
 2.
  2 L2 and  
LC 2 L
C
2L
2
2 2
2 2
R  L 
  L .
C
EVALUATE: VL is maximum at a frequency greater than the resonance frequency and X C is a maximum at a
frequency less than the resonance frequency. These frequencies depend on R , as well as on L and on C.
IDENTIFY: Follow the steps specified in the problem.
SET UP: In part (a) use Eq.(31.23) to calculate Z and then I  V / Z .  is given by Eq.(31.24). In part (b) let
Z  R  iX .
EXECUTE: (a) From the current phasors we know that Z  R 2  ( L  1 C )2 .
R2   2 L2 
31.75.
2


1
Z  (400 )   (1000 rad s)(0.50 H) 
  500 .
6
(1000
rad
s)(1.25

10
F)


V 200 V
I 
 0.400 A.
Z 500 
2
 (1000 rad s)(0.500 H)  1 (1000 rad s)(1.25 10 6 F) 
  L  1 (C ) 


arctan
(b)   arctan 
.

  36.9

400 
R






1
1 

(c) Zcpx  R  i   L 
. Z cpx  400   i  (1000 rad s)(0.50 H)  (1000 rad s)(1.25 106 F)   400   300 i.

C




Z  (400 )2  (300 ) 2  500 .
V
200 V
 8  6i 
 8  6i   8  6i 


 A  (0.320 A)  (0.240 A)i. I   25   25   0.400 A.
Z cpx (400  300i)   25 

 

Im( I cpx ) 6 25

 0.75    36.9.
(e) tan  
Re( I cpx ) 8 25
(d) I cpx 
 8  6i 
(f ) VRcpx  I cpx R  
 (400 )  (128  96i )V.
 25 
 8  6i 
VLcpx  iI cpx L  i 
 (1000 rad s)(0.500 H)  (  120  160i) V.
 25 
1
 8  6i 
 i
 (192  256i) V.

C  25  (1000 rad s)(1.25 106 F)
 VRcpx  VLcpx  VCcpx  (128  96i) V  (120  160i)V  (192  256i) V  200 V.
VCcpx  i
(g) Vcpx
I cpx
EVALUATE: Both approaches yield the same value for I and for  .