Download cis480-5

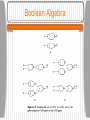
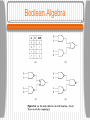
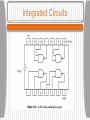
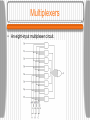
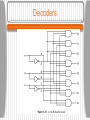
Gates
 A digital circuit is one in which only two
logical values are present.
• Typically, a signal between 0 and 0.5 volt represents
one value (e.g. binary 0) and a signal between 1 and
1.5 volts represents the other value (e.g. binary 1).
 Tiny electronic devices, called gates, can
compute various functions of these two-valued
signals.
• Gates form the basis on which all digital computers
are built.
Gates
 A transistor can be made to operate as a very
fast binary switch.
 The next slide shows a bipolar transistor (the
circle) embedded in a simple circuit. The
transistor has three connections to the outside:
 the collector
 the base
 the emitter
• When the Vin is below a certain critical value, the
transistor turns off and acts like an infinite
resistance. This causes Vout to to take on a value
close to Vcc.
Gates
• When Vin exceeds the critical value, the transistor
switches on and acts like a wire, causing Vout to be
pulled down to 0 volts.
• This circuit is an inverter, converting a logical 0 to a
logical 1, and vice versa. The resistor is needed to
limit the amount of current drawn by the transistor.
• In the next figure, if both inputs are high, the output
will be low. If either output is low, the output will
be high.
• In the third figure, the transistors are wired in
parallel rather than series. If either input is high, the
transistor will turn on and pull the output down.
Gates
Gates
 These three circuits form the three simplest
gates:
• NOT gates
• NAND gates
• NOR gates
 NOT gates are also called inverters.
 If we now adopt the convention that “high” is a
logical 1, and that “low” (ground) is a logical 0,
we can express the output values as a function
of the input values.
Gates
Gates
 If the output of the NAND gate is fed into an
inverter circuit, we get another circuit with
precisely the inverse of the NAND gate - an
AND gate.
 The NOR gate can be connected to an inverter
to yield an OR gate. The small circles used as
part of the symbols for the inverter etc. are
called inversion bubbles.
 The five gates described are the principal
building blocks of the digital logic level.
Gates
• NAND and NOR gates require two transistors each,
while the AND and OR gates require three
transistors each. Therefore, many computers are
based on NAND and NOR gates rather than AND
and OR.
• The two major technologies for constructing gates
are bipolar and MOS (Metal Oxide
Semiconductor). The major bipolar types are TTL
(Transistor-Transistor Logic) and ECL (EmitterCoupled Logic). MOS gates are slower than TTL
and ECL but require less power and space. Most
modern CPUs and memories use CMOS technology
which runs on +1.5 volts.
Boolean Algebra
 Boolean Algebra can be used to describe the
circuits that can be built by combining gates.
 A Boolean function has one or more input
variables and yields a result that depends only
those variables.
• Define a function f such that f(A) is 1 if A is 0 and
f(A) is 0 if A is 1. This function is the NOT function.
 Since a Boolean function of n variables has
only 2n possible combinations of inputs, the
function can be completely described by giving
a truth table with 2n rows of inputs/output.
The Majority Function
Boolean Algebra
 Although any Boolean function can be
specified by giving its truth table, this notation
becomes cumbersome as the number of
variables increases.
 Another notation is based on the fact that any
Boolean function can be specified by telling
which combinations of input variables give an
output value of 1.
• An apostrophe after an input variable means that its
value is inverted. The absence of an apostrophe
means that it is not inverted.
Boolean Algebra
 Implied multiplication (or a dot) means the
Boolean AND function and + means the
Boolean OR function.
• Example: AB’C takes the value 1 only when A = 1,
B = 0 , and C = 1.
• The previous truth table can be written as M =
A’BC + AB’C + ABC’ + ABC as a compact way of
giving the truth table.
• A function of n variables can be described by giving
a “sum” of at most 2n n-variable “product” terms.
Boolean Algebra
 The formulation of a Boolean function as a sum
of up to 2n products leads directly to a possible
implementation as shown.
• We can implement a circuit for any Boolean
function by:
 Writing down the truth table for the function
 Providing inverters to generate the complement of each
input
 Drawing an AND gate for each term with a 1 in the result
column
 Wiring the AND gates to the appropriate inputs
 Feeding the output of all the AND gates into an OR gate
Boolean Algebra
 It is often convenient to implement circuits
using only a single gate type.
 It is straightforward to convert circuits
generated by the previous algorithm to pure
NAND or pure NOR form - all we need is a
way to implement NOT, AND, and OR using a
single gate type.
 Both NAND and NOR gates are said to be
complete, because any Boolean function can be
computed using either of them.
Boolean Algebra
 No other gate has this property.
 Follow the previous algorithm then replace the
multi-input gates with equivalent circuits using
two-input gates. Replace the NOT, AND, and
OR gates with the circuits of the following
slide.
Boolean Algebra
Circuit Equivalence
 Circuit designers try to reduce the number of
gates to reduce cost, space, power consumption,
etc.
 To reduce the complexity, a circuit with fewer
gates which computes the same function must
be found. Boolean algebra can be a valuable
tool.
 Many rules of ordinary algebra hold for
Boolean algebra. AB + AC can be factored into
A(B + C) using the distributive law.
Circuit Equivalence
Circuit Equivalence
 In general, a designer starts with a Boolean
function and then applies the laws of Boolean
algebra to find a simpler but equivalent one.
From the final function, a circuit can be
constructed.
 Some of the major identifies from Boolean
algebra are shown in the following slide. Note
that each law has two forms that are duals of
each other. By interchanging AND and OR and
also 0 and 1, either form can be produced from
the other one.
Boolean Algebra
DeMorgan’s Law
 DeMorgan’s law can be extended to more than
two variables, for example, (ABC)’ = A’ + B’ +
C’.
 DeMorgan’s law suggests an alternative
notation. The following slide shows AND form
with negation indicated by inversion bubbles,
for both input and output. Thus an OR gate is
equivalent to a NAND gate.
 A NOR gate can be drawn as an AND gate with
inverted inputs.
DeMorgan’s Law
DeMorgan’s Law
 Using the identities of the previous slide and
the analogous ones for multi-input gates, it is
easy to convert the sum-of-products
representation of a truth table to pure NAND or
pure NOR form.
 The lines connecting the output of the AND
gates to the input of the OR gates should be
redrawn with two inversion bubbles.
 The OR gate can then be replaced with the
equivalent NAND gate.
Boolean Algebra
Circuit Equivalence
 The same physical gate can compute different
functions, depending on the conventions used.
 The following slide shows the output of a
certain gate F, for different input combinations.
• Both inputs and outputs are shown in volts.
• If we adopt the convention that 0 volts is logical 0
and 1.5 volts is logical 1, called positive logic, we
have one result. If, however, we adopt negative
logic, which has 0 volts as logical 1 and 1.5 volts as
logical 0, we get another function, the OR function.
Usually, we will assume positive logic.
Positive and Negative Logic
Integrated Circuits
 Gates are not manufactured or sold
individually, but rather in units called
Integrated Circuits, often called ICs or chips.
 An IC is a square piece of silicon on which
some gates have been deposited. Small ICs are
usually mounted in rectangular plastic or
ceramic packages which can be larger than the
die (2 x 2mm up to 18 x 18mm).
• Along the long edges are two parallel rows of pins
that can be inserted into sockets or soldered to
printed circuit boards.
Integrated Circuits
 The packages with two rows of pins outside
and ICs inside are technically known as Dual
Inline Packages or DIPs, but everyone calls
them chips.
 The most common packages have 14, 16, 18,
20, 22, 24, 28, 40, 64, or 68 pins. For large
chips, square packages with pins on all four
sides are often used.
 Chips can be divided into rough classes based
on the number of gates they contain:
Integrated Circuits
• SSI (Small Scale Integration) circuit: 1 to 10 gates.
• MSI (Medium Scale Integration) circuit: 10 to 100
gates.
• LSI (Large Scale Integration) circuit: 100 to 100,000
gates.
• VLSI (Very Large Scale Integration) circuit:
>100,000 gates.
 An SSI chip typically contains two to six
independent gates, each of which can be used
independently. The package generally has a
notch near pin 1 to identify the orientation.
Integrated Circuits
•Common types of integrated-circuit packages,
including a dual-inline package (a), pin grid array
(b), and land grid array (c).
Integrated Circuits
Integrated Circuits
 Many chips like this are available for a few
cents each. In the 1970s, computers were
constructed out of a large number of these
chips. Today multiple CPUs and cache memory
are etched onto a single chip.
 We can consider all gates to be ideal so that
output appears as soon as input is applied. In
reality chips have a finite gate delay which
includes signal propagation time and switching
time. Typical delays are 100 picoseconds to
10nsec.
Combinatorial Circuits
 Many applications of digital logic require a
circuit with multiple inputs and multiple
outputs in which the outputs are uniquely
determined by the current inputs. Such a circuit
is called a combinatorial circuit.
 Not all circuits have this property (e.g. memory
elements). A circuit implementing a truth table
is a typical example of a combinatorial circuit.
Multiplexers
 A multiplexer is a circuit with 2n data inputs,
one data output and n control inputs that select
one of the data inputs.
• A multiplexer can be also be used to implement the
majority function shown previously. For each
combination of A, B, and C, one of the data input
lines is selected. Each input is wired to either Vcc
(logical 1) or ground (logical 0).
 Input Di is the same as the value in row i of the truth table.
• A demultiplexer routes its single input signal to one
of 2n outputs, depending on the values of the control
lines.
Multiplexers
• An eight-input multiplexer circuit.
Multiplexers
Decoders
• A decoder takes an n-bit number as input
and uses it to select (i.e. set to 1) exactly
one of the 2n output lines.
• A decoder can be used, for example, to
select 1 of 8 memory chips given the highorder 3 bits of the address if the chips are
organized so that chip 0 has addresses 0 to
256 MB, chip 1 has addresses 256 MB to
512 MB, and so on.
Decoders