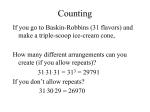Download Math 1004: Probability

Announcements
Finite Probability
Wednesday, September 14th
I
MyMathLab 2 is due tonight!
I
Problem Set 2 is due Friday Sept 16
Today: Sec. 5.5: Combinations and Permutations I
Recognize combinations or permutations situations
Use the combinations/permutations formulas to solve
counting problems
Next Class: Sec. 5.5: Combinations and Permutations II
Cherveny
Sept 14
Math 1004: Probability
Informal Permutations vs Combinations
Permutations: Want to count ways to choose objects without
replacement and the order chosen matters.
Example
There are 8 paintings. How many ways can you arrange 5 of them
in a row on the wall?
Combinations: Want to count ways to choose objects without
replacement but the order chosen does not matter.
Example
There are 10 people in a family. How many ways can five of them
go to the park?
Cherveny
Sept 14
Math 1004: Probability
Deciding Permutations or Combinations Practice
Decide if it’s appropriate to use combinations or permutations in
the following computations:
1. The number of ways to stack three different flavors of ice
cream from 29 flavors on a cone. Permutations
2. The number of stock ticker symbols for which each
abbreviation consists of four letters. Neither
3. The number of ways a five card hand can be dealt from a
standard 52 card deck. Combinations
4. The number of ways to make a 9 person batting lineup for a
baseball team from a roster of 14 players. Permutations
5. The number of ways the 30 people in the class can sit in the
45 seats available. Permutations
6. The number of 16 digit credit card numbers that are possible.
Neither
Cherveny
Sept 14
Math 1004: Probability
Permutations
Let’s be more precise:
Definition
Permutations The number of ways r objects can be chosen from
a collection of n objects without replacement if order chosen
matters is called P(n, r ) and given by
P(n, r ) =
n!
(n − r )!
Recall: The ! means “factorial”. For instance,
6! = 6 · 5 · 4 · 3 · 2 · 1 = 720
Cherveny
Sept 14
Math 1004: Probability
Combinations
Definition
Combinations The number of ways r objects can be chosen from
a collection of n objects without replacement if order chosen does
not matter is called C (n, r ) and given by
C (n, r ) =
P(n, r )
n!
=
r!
r !(n − r )!
Note: Another common way of writing C (n, r ) is
Cherveny
Sept 14
Math 1004: Probability
n
r
.
Practice
1. How many different selections of two books can be made from
nine books?
2. How many different ways can a president, treasurer, and
secretary be chosen from a class of 15 students?
3. At a party, everyone shakes hands with everyone else. If 45
handshakes take place, how many people are at the party?
4. How many ways can no more than 3 people from a 5 person
family go to the grocery store?
Answers:
1. C (9, 2) = 36
2. P(15, 3) = 2730
3. If there are N people at the party, there are C (N, 2)
handshakes. Expanding C (N, 2) = 45 gives N 2 − N − 90 = 0,
which factors as (N − 10)(N + 9) = 0. The only solution that
makes sense is N = 10.
4. C (5, 1) + C (5, 2) + C (5, 3) = 5 + 10 + 10 = 25
Cherveny
Sept 14
Math 1004: Probability