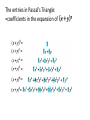* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Patterns and Combinatorics
Survey
Document related concepts
Transcript
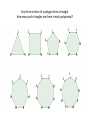
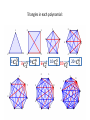
Patterns and Combinatorics Pascal’s Triangle Pascal’s Triangle: click to see movie 210 210 Triangular numbers Triangular numbers: short formula: Proof: Here n=4: For each polynomial, connect all pairs of vertices by lines. Some of these lines will be the sides, some will be diagonals. How many such lines are there in total in each polynomial? 1 2 1 2 1 2 2 3 3 4 1 2 2 7 3 5 3 4 5 1 2 7 6 6 4 1 8 5 3 4 3 6 4 5 1 9 3 8 4 7 5 6 We counted all lines connecting the vertices of the polygons: Can you explain the pattern? 1 2 1 1 2 5 2 3 2 3 lines 3 4 6 lines +3 +4 2 1 3 6 4 3 1 4 10 lines 5 15 lines +5 1 1 9 2 2 7 3 8 3 3 6 4 +6 21 lines 7 4 5 5 +7 28 lines 8 4 6 7 5 +8 6 36 lines The number of lines connecting the vertices of a polygon with n sides is the (n-1) triangular number: 2 The n-th vertex contributes n-1 red lines: 1 3 4 also denoted Counts how many pairs of 2 vertices we can form from among n vertices. Each pair determines a line. Cont the rows in Pascal’s triangle starting from 0. The entry on the n-th horizontal row, and k-th slanted row in Pascal’s triangle: = number of ways to choose a set of k objects from among n given objects. 1= = 1= 1= 1= 1= 5th horizontal row 1= 3= 3= 6= 10= 2nd slanted row 1= 2= 4= 5= 1= 1= 4= 10= 1= 5= 1= Any three vertices of a polygon form a triangle. How many such triangles are there in each polynomial? 1 2 1 2 1 2 2 3 3 4 1 2 2 7 3 5 3 4 5 1 2 7 6 6 4 1 8 5 3 4 3 6 4 5 1 9 3 8 4 7 5 6 Triangles in each polynomial: 1 2 1 1 2 5 2 3 2 1= 3 4 4= 3= 10= 6= 2 1 3 6 4 3 1 4 5 20= 10= 1 1 9 2 2 7 3 8 3 3 6 4 5 7 4 5 6 8 4 7 5 6 Patterns for the number of triangles in a polynomial of n+1 sides: In general, we count: Triangles formed with the vertices 1, 2, ..., n+1 Triangles formed with the vertices 1, 2, ..., n Triangles formed with the vertex n+1 and a pair of other vertices among 1, 2, ..., n More generally: Suppose there are n+1 people in your class. In how many ways can a group of k+1 people be chosen? Ways to choose a random group of k+1 people Ways to choose a group of k+1 people if you’re not included Ways to choose a group of k+1 people if you’re not included (it remains to choose k other people from the remainder of the class) The entries in Pascal’s Triangle: =coefficients in the expansion of Think about: Sums