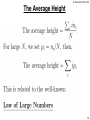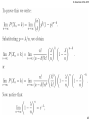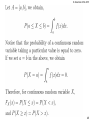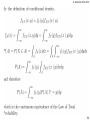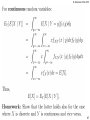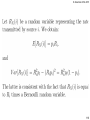Download Basic Probability Topics - Department of Electronic Engineering

© Zukerman 2014-2015
Basic Probability Topics
Moshe Zukerman
Electronic Engineering Department
City University of Hong Kong
Hong Kong SAR, PRC
1
Text/Reference Books
© Zukerman 2014-2015
Moshe Zukerman, Introduction to Queueing
Theory and Stochastic Teletraffic Models
(Chapter 1)
http://www.ee.cityu.edu.hk/~zukerman/classnotes.pdf
D. Bertsekas and J. N. Tsitsiklis, Introduction to
Probability, Athena Scientific, Belmont,
Massachusetts 2002.
S. M. Ross, A first course in probability,
Macmillan, New York, 1976.
2
Events, Sample Space,
and Random Variables
© Zukerman 2014-2015
• Consider an experiment (e.g. tossing a coin, or rolling
a die).
• Sample space - set of all possible outcomes.
• Event - a subset of the sample space.
• example: experiment consisting of rolling a die once.
Sample space = {1, 2, 3, 4, 5, 6}
Possible events:
• {2, 3},
• {6},
• empty set {} (often denoted by Φ)
• the entire sample space {1, 2, 3, 4, 5, 6}
3
© Zukerman 2014-2015
4
© Zukerman 2014-2015
5
Events are called mutually exclusive if
their intersection is the empty set.
© Zukerman 2014-2015
A set of events is exhaustive if its union is equal to the
sample space.
Example 1: tossing a coin only once
The events {H} (Head) and {T} (Tail) are both
mutually exclusive and exhaustive.
What is the state space (the set) of all possible events
in this case?
Example 2: rolling a die only once
The events {1}, {2}, {3}, {4}, {5}, and {6} are both
mutually exclusive and exhaustive.
The events {4}, {5}, and {6} are mutually exclusive but
are not exhaustive.
6
© Zukerman 2014-2015
A random variable is a real valued function defined on
the sample space.
This function X = X(ω) assigns a number to each
outcome ω of the experiment.
Example: tossing a coin experiment
X = 1 for Head {H}
X = 0 for Tail {T}
Note that the function X is deterministic (not random),
but the ω is unknown before the experiment is
performed. Therefore X(ω) is called a random variable.
7
© Zukerman 2014-2015
8
© Zukerman 2014-2015
Probability, Conditional Probability
and Independence
Consider a sample space S. Let A be a subset of S.
The probability of A is the function on S and all its
subsets, denoted P(A) that satisfies the following
three axioms:
3. The probability of the union of mutually exclusive
events is equal to the sum of the probabilities of
these events.
9
© Zukerman 2014-2015
10
© Zukerman 2014-2015
One intuitive interpretation of probability of
an event is its limiting relative frequency
11
© Zukerman 2014-2015
Number of People
30
25
20
15
10
5
0
141-150 cm
151-160 cm
161-170 cm
171-180 cm
181-190 cm
Height
An example of a Histogram with 5 ranges
(bins) and each range is 10 cm.
In every range (bin), 10 ni values are added up.
In this case, N = 93 people.
12
© Zukerman 2014-2015
Limiting Relative Frequency (continued)
13
© Zukerman 2014-2015
The Average Height
14
© Zukerman 2014-2015
Conditional Probability
15
© Zukerman 2014-2015
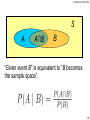
S
A
A∩B
B
“Given event B” is equivalent to “B becomes
the sample space”.
16
© Zukerman 2014-2015
Example: consider rolling a die and B={1,2,3}
(B = outcome is 1 or 2 or 3), and A={1}, then
Now, since
we obtain
17
© Zukerman 2014-2015
Events A and B are said to be independent
if and only if
Equivalent definitions are:
Independence between two events means that if one
of them occurs, the probability of the other to occur is
not affected.
Homework: Show the equivalence between these
three relationships.
18
© Zukerman 2014-2015
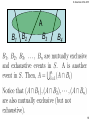
B1
B2
A
B3
B4
19
© Zukerman 2014-2015
20
© Zukerman 2014-2015
Other names for Bayes’ Theorem: Bayes' law
and Bayes' rule
Homework: Make sure you know how to derive the
law of total probability and Bayes’ theorem.
21
© Zukerman 2014-2015
22
© Zukerman 2014-2015
23
© Zukerman 2014-2015
24
© Zukerman 2014-2015
25
© Zukerman 2014-2015
26
© Zukerman 2014-2015
27
© Zukerman 2014-2015
28
© Zukerman 2014-2015
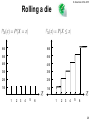
Rolling a die
6/6
6/6
5/6
5/6
4/6
4/6
3/6
3/6
2/6
2/6
1/6
1/6
1
2
3
4
5
6
1
2
3
4
5
6
29
© Zukerman 2014-2015
For the case of Rolling a die
6/6
5/6
4/6
3/6
2/6
1/6
1
2
3
4
5
6
30
© Zukerman 2014-2015
31
© Zukerman 2014-2015
A random variable is called discrete if it takes at
most a countable number of possible values.
A continuous random variable takes an uncountable
number of possible values.
For discrete random variables
the joint probability function is:
and the probability function of a single discrete
random variable is:
32
Conditional Probability for
Discrete Random Variables
© Zukerman 2014-2015
Because of the above and since
we obtain
The implication is that the event {Y=y} is the new
sample space and X has a legitimate distribution
function in this new sample space.
is another version of the law of total probability.
33
© Zukerman 2014-2015
34
© Zukerman 2014-2015
Example
You roll a fair 6-side die twice. X is a result of the
first roll and Y is the result of the second roll.
Define U = max(X,Y) and V = min(X,Y).
Find: P(U=5|V=3)
35
© Zukerman 2014-2015
Convolution
36
© Zukerman 2014-2015
Question
Explain the last equation of convolution
using the Law of Total Probability.
37
© Zukerman 2014-2015
Now consider k random variables
The convolution of the k probability functions is:
38
Some discrete random variables
© Zukerman 2014-2015
1. Bernoulli
2. Geometric
39
© Zukerman 2014-2015
3. Binomial
The number of successes in n independent Bernoulli trials
Can be used to model users activity.
A user is active with probability p and non-active with
probability 1-p.
X = i is the event where i users are active.
40
© Zukerman 2014-2015
4. Poisson
How to compute these values?
Use Recursion and start from values around λ.
Set arbitrary initial value then normalize.
41
© Zukerman 2014-2015
Poisson-Binomial Relationship
42
© Zukerman 2014-2015
43
© Zukerman 2014-2015
44
Sum of two Poisson
Random variables
© Zukerman 2014-2015
45
© Zukerman 2014-2015
5. Pascal
46
© Zukerman 2014-2015
6. Discrete Uniform
47
© Zukerman 2014-2015
Continuous Random Variables and Distributions
48
© Zukerman 2014-2015
49
© Zukerman 2014-2015
50
© Zukerman 2014-2015
51
© Zukerman 2014-2015
52
© Zukerman 2014-2015
Example
53
© Zukerman 2014-2015
Please complete all steps in the following.
54
© Zukerman 2014-2015
Convolution of continuous random variables
55
© Zukerman 2014-2015
Convolution of k continuous random variables
56
© Zukerman 2014-2015
57
© Zukerman 2014-2015
Some Continuous Random Variables
1. Uniform
(with parameters a,b)
58
© Zukerman 2014-2015
Inverse transform sampling
Using uniform (0,1) deviates to generate sequence
of random deviates of any distribution
59
© Zukerman 2014-2015
60
© Zukerman 2014-2015
61
© Zukerman 2014-2015
Convolution of two independent
uniform (0,1) random variables
1
1
2
62
© Zukerman 2014-2015
2. Exponential
(with parameter µ)
63
© Zukerman 2014-2015
Example
Show how to apply the Inverse transform sampling
to generate exponential deviates.
Guide
64
© Zukerman 2014-2015
65
© Zukerman 2014-2015
66
© Zukerman 2014-2015
67
© Zukerman 2014-2015
68
© Zukerman 2014-2015
69
© Zukerman 2014-2015
70
© Zukerman 2014-2015
71
© Zukerman 2014-2015
72
© Zukerman 2014-2015
73
© Zukerman 2014-2015
74
© Zukerman 2014-2015
75
© Zukerman 2014-2015
76
© Zukerman 2014-2015
77
© Zukerman 2014-2015
78
© Zukerman 2014-2015
79
© Zukerman 2014-2015
80
© Zukerman 2014-2015
81
© Zukerman 2014-2015
82
© Zukerman 2014-2015
83
© Zukerman 2014-2015
84
© Zukerman 2014-2015
85
© Zukerman 2014-2015
86
© Zukerman 2014-2015
87
© Zukerman 2014-2015
88
© Zukerman 2014-2015
89
© Zukerman 2014-2015
90
© Zukerman 2014-2015
91
© Zukerman 2014-2015
92
© Zukerman 2014-2015
93
© Zukerman 2014-2015
94
© Zukerman 2014-2015
95
© Zukerman 2014-2015
96
© Zukerman 2014-2015
97
© Zukerman 2014-2015
98
© Zukerman 2014-2015
99
© Zukerman 2014-2015
100
© Zukerman 2014-2015
101
© Zukerman 2014-2015
102
© Zukerman 2014-2015
103
© Zukerman 2014-2015
104
© Zukerman 2014-2015
105
© Zukerman 2014-2015
Homework:
Observe the following behavior of the
Poisson probability function and provide
explanation.
106
© Zukerman 2014-2015
Probability
Poisson Probability function with λ= 1
Number of arrivals
Credit: Li Fan
107
© Zukerman 2014-2015
Probability
Poisson Probability function with λ= 10
Number of arrivals
Credit: Li Fan
108
© Zukerman 2014-2015
Probability
Poisson Probability function with λ= 100
Number of arrivals
Credit: Li Fan
109
© Zukerman 2014-2015
Probability
Poisson Probability function with λ= 1000
Number of arrivals
Credit: Li Fan
110
© Zukerman 2014-2015
Probability
Poisson Probability function with λ= 10000
Number of arrivals
Credit: Li Fan
111
© Zukerman 2014-2015
112
© Zukerman 2014-2015
113
© Zukerman 2014-2015
114
© Zukerman 2014-2015
115
© Zukerman 2014-2015
116
© Zukerman 2014-2015
117
© Zukerman 2014-2015
118
© Zukerman 2014-2015
119
© Zukerman 2014-2015
120
© Zukerman 2014-2015
121
© Zukerman 2014-2015
122
© Zukerman 2014-2015
123