Download Practice A - rjssolutions.com

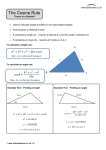
Name ———————————————————————
LESSON
2.3
Date ————————————
Practice A
For use with pages 88–95
Use the Law of Detachment to make a valid conclusion in the situation.
1. If you get a hit, then your baseball team will win. You hit a home run.
You get a hit
2. If Rylee gets promoted, then Callie will also be promoted. Rylee is promoted.
3. If two integers are added together, then the result is an integer. You add an integer x
to another integer y.
4. If you double a negative number, then the result is a smaller number. You calculate
2x, where x < 0.
2x u
than x.
5. If an integer is divided by one of its factors, then the result is another one of the
integer’s factors. You divide an even integer x by 2.
Use the Law of Syllogism to write the statement that follows from the
pair of statements that are given.
6. If Moose is hungry when he goes to the pizza shop, then he’ll finish a whole pizza.
If Moose eats a whole pizza, then he goes through a pitcher of juice.
arrives by tomorrow, then you won’t be charged a late fee.
8. If a triangle has two angles of 608, then the triangle is equiangular. If a triangle is
equiangular, then it is also equilateral.
Decide whether the conclusion reached from the two statements
demonstrates the Law of Detachment, the Law of Syllogism, or neither.
9. If Cedric plays in a big game, then he gets nervous. If Cedric gets nervous, then he
performs well.
LESSON 2.3
Copyright © Holt McDougal Math. All rights reserved.
7. If you mail the payment by noon, then it will arrive by tomorrow. If your payment
Conclusion: If Cedric plays in a big game, then he performs well.
10. If Leanne spends more than $30 on her car, then she’ll have to wait until next week
to buy Michael’s birthday gift. Leanne spent $40 on her car.
Conclusion: Leanne will have to wait until next week to buy Michael’s birthday gift.
Geometry
IDEA! Works
27
Name ———————————————————————
LESSON
2.3
Practice A
Date ————————————
continued
For use with pages 88–95
Decide whether inductive or deductive reasoning is used to reach the
conclusion.
11. While shopping, you notice that brand A is more expensive than brand B. You
conclude that brand A is of higher quality than brand B.
12. Because the brand A product costs $1.50 and the brand B product costs $1.00, you
conclude that the brand A product is 50% more expensive.
13. On the first meet of the year, JD, Bob, and Raul finish their race in a tie. In the final
meet of the year, Raul finishes well ahead of Bob and JD. Having seen both races,
you conclude that Raul trained the hardest.
In Exercises 14 and 15, use the figure at the right.
14. Based on what you see in the figure, use inductive
reasoning to make a conjecture about how the area
of one square compares to the area of another square
with sides that are twice as long.
15. Use deductive reasoning to prove your conjecture by
using side lengths of s 5 x and s 5 2x in the formula for
the area of a square and comparing the result.
Use the figure showing three standing dominos, A, B, and C.
16. Is the Law of Detachment or the Law of Syllogism
B
Statements: If A is pushed into B, then B will be
knocked into C. A is pushed into B.
LESSON 2.3
Conclusion: B is knocked toward C.
28
Geometry
IDEA! Works
A
Copyright © Holt McDougal Math. All rights reserved.
C
used to reach the conclusion below?
ANSWERS
Practice A
1. Your team wins the baseball game. 2. Callie
is also promoted. 3. The sum is an integer.
4. 2x < x 5. The quotient is a factor of x. 6. If
Moose is hungry when he goes to the pizza shop,
then he drinks a pitcher of soda. 7. If you mail
the payment by noon, then you won’t be charged
a late fee. 8. If a triangle has two angles of 608,
then it is equilateral. 9. Law of Syllogism
10. Law of Detachment
11. inductive; the conclusion is a conjecture based
on your perception from a specific example.
12. deductive; the conclusion is based on a
computation of the actual percent using the given
values. 13. inductive; the conclusion is a conjecture drawn on your race observations rather than
on the actual training effort. 14. The area of one
square is one-fourth of the area of another square
with sides that are twice as long.
1
15. A1 5 s2 5 x 2, A2 5 (2x)2 5 4x 2; A1 5 } A2
4
16. Law of Detachment
Quiz 1
1. sample answer: (22)(25) 5 10 2. sample
answer: 2 1 3 5 5 3. If-then form: If an angle
is a straight angle, then its measure is 1808.
Converse: If the measure of an angle is 1808, then
the angle is a straight angle. Inverse: If an angle is
not a straight angle, then its measure is not 1808.
Contrapositive: If the measure of an angle is not
1808, then it is not a straight angle. 4. If-then
form: If a polygon is a quadrilateral, then it has
4 sides. Converse: If a polygon has 4 sides, then
it is a quadrilateral. Inverse: If a polygon is not
a quadrilateral, then it does not have 4 sides.
Contrapositive: If a polygon does not have 4 sides,
then it is not a quadrilateral.
5. 8 1 7 > 11 6. You can purchase Joe’s bicycle.
7. If the measure of an angle is less than 90° ,
then the angle is an acute angle. 8. If an angle
is not an acute angle, then its measure is not less
than 90°.
Lesson 2.4
Practice A
1. 5 2. 8 3. 9 4. 6 5. 6 6. 10 7. 8 8. 9
9. Through the two points A and B, there exists
A4
Geometry
IDEA! Works
exactly the one line, q. 10. Line q contains at
least the two points A and B. 11. Lines p and q
intersect in exactly the one point A. 12. Through
the three
noncollinear points C, D, and E, there exists only
the one plane S. 13. Plane S contains at least the
three noncollinear points C, D, and E.
14. Sample answer: The two points D and E lie in
plane R, so the line m that contains them lies in R.
15. The intersection of planes R and S is line m.
16. no 17. no 18. yes 19. no
20. Sample answer:
21. Sample answer:
B
R
P
A
T
S
22. yes; directly indicated by right angle symbol
23. yes; @##$
EF ⊥ plane S, so it is ⊥ to every line in
S that it intersects 24. no; can’t assume
collinearity without the line drawn
25. yes; all 3 points are on one line
26. yes; it is obvious in diagram
27. no; can’t assume that @##$
DH intersects @##$
EF
28. yes; @##$
EF ⊥ to every line in plane S that it
intersects 29. no; can’t assume these lines
⊥ without a rt. angle marked
Problem Solving Workshop:
Mixed Problem Solving
1. a. The amount of bacteria doubles after every
hour. b. 768 billion bacteria
2. a. Inductive reasoning; it is based on a pattern
in the data. b. Deductive reasoning; you are using
values that are given on the graph.
3. Answers will vary. 4. a. may not; You can
write the statement as “If Adam lives at Pine
Meadows, then he is not allowed to have a dog.”
b. may have; All you know is that Jodi was in Utah
and the Zion National Park is in Utah. You do not
know if she visited it. 5. 43
Lesson 2.5
Practice A
1. a. Addition Property of Equality b. Division
Property of Equality 2. a. Subtraction Property
of Equality b. Addition Property of Equality
c. Division Property of Equality
Copyright © Holt McDougal Math. All rights reserved.
Lesson 2.3