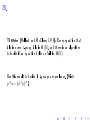Download slides

Finite Models and Practical Decision
Procedures in Propositional Substructural
Logics I
Peter Jipsen
Chapman University, Orange, California
CUSO Winter School, 28 Jan 2013, Les Diablerets
1. Groups
G = (G , ·, − , 1) is a group if (xy )z = x (yz )
1
x −1 x
=1
and
Prove that xx
−1
1x
=1
=x
and x 1
Show that the identities
for all x , y , z
=x
hold
(xy )z = x (yz ),
do not suce to dene groups
∈G
x −1 x
=1
and x 1
=x
2. Monoids
M = (M , ·, 1) is a monoid if (xy )z = x (yz )
x1
=x
and
1x
=x
for all x , y , z
A monoid is commutative if xy
= yx
∈M
holds
Find a smallest noncommutative monoid
3. Join-semilattices and partial orders
A = (A, ∨) is a (join-)semilattice if (x ∨ y ) ∨ z = x ∨ (y ∨ z )
x
∨y =y ∨x
Dene x
≤y
Prove that
x
≤
x
and
i x
∨x =x
for all x , y , z
∈A
∨y =y
is a partial order, i.e., x
≤ y & y ≤ x =⇒
x
=y
A partial order is linear if x
and
≤y
x
or y
≤ x,
≤ y & y ≤ z =⇒
≤x
for all x , y .
Find the smallest nonlinear join-semilattice.
x
≤z
4. Quasi-identities for semilattices?
Suppose
A = (A, ∨, ≤) satises
x
≤z
x
≤ y =⇒
x
≤y ∨z
x
≤ z =⇒
x
≤y ∨z
and y
≤ z =⇒
Does it follow that
x
∨y ≤z
and
(A, ∨)
≤
is a poset
is a semilattice?
5. Lattices
A = (A, ∧, ∨) is a lattice if
(x ∧ y ) ∧ z = x ∧ (y ∧ z ),
x
∧ y = y ∧ x,
(x ∧ y ) ∨ x = x ,
(x ∨ y ) ∨ z = x ∨ (y ∨ z ),
x
∨ y = y ∨ x,
(x ∨ y ) ∧ x = x
These are called the associative, commutative and absorbtive
laws for meet and join respectively.
Prove that x
Show that x
∧x =x
holds in every lattice
∧ (y ∨ z ) = ( x ∧ y ) ∨ (x ∧ z )
fails in some lattice.
6. Distributivity
Prove the following are equivalent:
(i) x
∧ (y ∨ z ) = (x ∧ y ) ∨ (x ∧ z )
(ii) x
∨ (y ∧ z ) = (x ∨ y ) ∧ (x ∨ z )
(iii) x
∧y =x ∧z
and x
∨ y = x ∨ z =⇒
y
=z
(iv) x
∧y ≤x ∧z
and x
∨ y ≤ x ∨ z =⇒
y
≤z
(i) and (ii) are called the distributive identities
7. Residuated Lattices
A = (A, ∧, ∨, ·, 1, \, /) is a residuated lattice if
(A, ∧, ∨)
(A, ·, 1)
is a lattice
is a monoid and
the residuation property xy
for all x , y , z
≤z
i y
≤ x \z
i x
≤ z /y
∈A
Order of operations:
stronger than
∧, ∨
Prove that
1
·
≤ x \x
stronger than
x (x \y )
\, /
≤y
and they bind
x
≤ y \yx
holds
Prove that xy \z
x (y
= y \(x \z )
∨ z ) = xy ∨ xz
(x ∨ y )z = xz ∨ yz
(x ∨ y )\z =
x \(y
∧ z) =
(x \y )/z = x \(y /z )
8. RL is an equational class
Prove that the residuation property can be expressed by 4
identities
hence the class RL of residuated lattices is an equational class
so it is closed under homomorphic images, subalgebras and
direct products
9. Integrality
A residuated lattice is integral if 1 is the top element, i.e.,
x
≤1
holds
Prove that xy
≤x ∧y
residuated lattice
and x \x
=1
hold in every integral
10. Bounded Residuated Lattices
A = (A, ∧, ∨, ·, 1, 0, \, /) is a bounded residuated lattice if
(A, ∧, ∨, ·, 1, \, /)
is a residuated lattice and 0 is the bottom
element
i.e.
0
≤x
Prove that 0x
holds for all x
= 0 = x0
∈A
and x
≤ 0\0
hence 0\0 is the top element, also denoted by
>
11. Divisibility
A residuated lattice
x
A is divisible if
≤ y =⇒ ∃u , v (x = uy
and x
= yv )
for all x , y
∈A
A divisible residuated lattice is called a generalized Basic Logic
algebra (or GBL-algebra)
Prove that divisibility is equivalent to
x
≤ y =⇒
x
= (x /y )y = y (y \x )
Prove this is equivalent to two equations
12. Meet is denable in IGBL-algebras
A be an integral residuated lattice
Prove that A is a GBL-algebra i x ∧ y = (x /y )y = y (y \x )
Let
13. Bounded implies integral
Prove that every bounded GBL-algebra is integral
14. GBL-algebras are distributive
*Prove that every GBL-algebra satises the distributive
identities
15. Prelinearity
A residuated lattice is prelinear if it satises the identities
x \y
∨ y \x ≥ 1
and x /y
∨ y /x ≥ 1
Prove that they are not equivalent
16. Commutative Residuated Lattices
A residuated lattice is commutative if it satises the identity
xy
= yx
Prove that this is equivalent to x \y
In this case we dene x
= y /x
→ y = x \y
*Prove that subdirectly irreducible commutative residuated
lattices are linearly ordered i they satisfy the identity
1
= ((x → y ) ∧ 1) ∨ ((y → x ) ∧ 1)
17. Denition of BL-algebra
A Basic Logic algebra (or BL-algebra) is a
bounded (hence integral) commutative prelinear GBL-algebra
Dene a negation by
Prove that
¬x = x → 0
¬1 = 0, ¬0 = 1
and x
≤ ¬¬x
18. The standard product algebra
⊆ R be the
= max(x , y )
Let [0, 1]
x
∨y
xy
=
unit interval, x
∧ y = min(x , y ),
multiplication of x , y
Find a denition for x
→y
such that
P = ([0, 1], ∧, ∨, ·, 1, 0, →) is a bounded residuated lattice,
called
the standard product algebra.
Prove that
P is a BL-algebra
This is an algebraic model of a fuzzy logic
19. MV-algebras
A multi-valued algebra (or MV-algebra) is a BL-algebra that
satises
¬¬x = x
Find the smallest BL-algebra that is not an MV-algebra
Prove that MV-algebras are self-dual, i.e.,
they satisfy DeMorgan's identity
(or equivalently
if
x
¬(x ∧ y ) = ¬x ∨ ¬y
¬(x ∨ y ) = ¬x ∧ ¬y )
and
A is an MV-algebra and one denes x ⊕ y = ¬(¬x · ¬y ) and
y = ¬x · y
(A, ∨, ∧, ⊕, 0, 1, )
map x 7→ ¬x
then
the
is an MV-algebra isomorphic to
A via
20. Boolean algebras
A = (A, ∧, ∨, ¬, 0, 1) is a Boolean algebra if (A, ∧, ∨) is a
bounded distributive lattice
and x
∧ ¬x = 0
Dene x
and x
∨ ¬x = 1
→ y = ¬x ∨ y
an MV-algebra
for all x
and prove that
∈A
(A, ∧, ∨, ∧, 1, 0, →)
is
21. The standard MV-algebra
([0, 1], ∧, ∨) be
= max(x + y − 1, 0)
Again let
xy
Find a denition for x
the unit interval lattice and dene
→y
such that
L = ([0, 1], ∧, ∨, ·, 1, 0, →) is a bounded residuated lattice
Prove that
L is an MV-algebra
This algebra is named after Šukasiewicz and is an algebraic
model of a fuzzy logic
22.
Heyting algebras
A Heyting algebra is a bounded residuated lattice that satises
xy
=x ∧y
Prove that Heyting algebras are commutative integral
GBL-algebras
Prove that xy
=x ∧y
residuated lattices
is equivalent to xx
=x ≤1
for
23.
Gödel algebras
A Gödel algebra is a prelinear Heyting algebra
Find the smallest Heyting algebra that is not prelinear
24. Triangular norms
Show that
I = ([0, 1], ∧, ∨, ∧, 1, 0, →) is a Gödel algebra for a
suitably dened operation
→
A t-norm is a commutative monoid
([0, 1], ·, 1)
such that
·
is
order-preserving,
i.e., x
≤ y =⇒
xz
≤ yz
A t-norm is continuous if lim xb
x →a
Note that the algebras
= ab
for all a, b
∈ [0, 1]
P, L and I have continuous t-norms as
fusion operation
Prove that a t-norm satises
i
·
has a residual
→
Prove it is continuous i
·
lim xb
x →a−
= ab
for all a, b
has a residual and satises
divisibility
Hence
([0, 1], ∧, ∨, ·, 1, 0, →)
continuous t-norm
is a BL-algebra i
·
is a
∈ [0, 1]
25. Lattice-ordered Groups
G = (G , ∧, ∨, ·, − , 1) is a lattice-ordered group (or `-group) if
1
(G , ∨)
is a join-semilattice,
identities x (y
Prove that
as well as
(G , ·, − , 1)
∨ z ) = xy ∨ xz
(G , ∧)
1
and x
is a group and the
∧ y = (x − ∨ y − )−
1
1
1
hold
is a semilattice, both absorption laws hold
(x ∨ y )z = xz ∨ yz ,
(x ∧ y )z = xz ∧ yz ,
x
x (y
∧ z ) = xy ∧ xz ,
∧ (y ∨ z ) = ( x ∧ y ) ∨ (x ∧ z )
hold
Prove that every bounded (hence every nite) lattice-ordered
group has only one element
Give an example of a commutative lattice-ordered group
26. `-groups are GBL-algebras
Let
G be an `-group and dene x \y = x − y and x /y = xy −
Prove that
1
(G , ∧, ∨, ·, 1, \, /)
is a GBL-algebra
1
27.
= {f : R → R | f
≤ y =⇒ f (x ) ≤ f (y )}
Let A(R)
x
Prove that
is 1-1 and onto and
A(R) = (A(R), ∧, ∨, ◦, − , id ) is a lattice-ordered
1
group
with f
◦g =
the composition of f and g
f −1 the inverse function of f ,
the identity function as id ,
f
∧g
dened by
(f ∧ g )(r ) = min(f (r ), g (r ))
f
∨g
dened by
(f ∨ g )(r ) = max(f (r ), g (r ))
and
28.
Theorem [Holland and McCleary 1979]: Every equation that
fails in some `-group fails in A(R), and there is an algorithm
to decide if an equation holds or fails in A(R)
Use this result to decide if
y −1 x = (x −1 y )−1 .]
`-groups
are prelinear. [Hint:
29. Direct decomposition of GBL-algebras
Theorem [Galatos and Tsinakis 2006]: Every GBL-algebra is
isomorphic to a direct product of an
`-group
and an integral
GBL-algebra
Use this result to prove that x (y
∧ z ) = xy ∧ xz
in every
GBL-algebra
∧ y = x (x \y ) = y ∧ x = y (y \x )
show that xy ∧ xz ≤ x (y ∧ z )
Hint: use the fact that x
xy \z
= y \(x \z )
to
and
30. A Sequent Calculus for RL
Show that the following quasi-identities hold in all residuated
lattices:
≤ z and uyv ≤ z =⇒ u (x ∨ y )v ≤ z
x ≤ y =⇒ x ≤ y ∨ z ,
x ≤ z =⇒ x ≤ y ∨ z
x ≤ y and x ≤ z =⇒ x ≤ y ∧ z
uxv ≤ z =⇒ u (x ∧ y )v ≤ z ,
uyv ≤ z =⇒ u (x ∧ y )v ≤ z
x ≤ y and z ≤ w =⇒ xz ≤ yw
x ≤ y and uzv ≤ w =⇒ ux (y \z )v ≤ w
x ≤ y and uzv ≤ w =⇒ u (z /y )xv ≤ w
xy ≤ z =⇒ y ≤ x \z ,
xy ≤ z =⇒ x ≤ z /y
(xy )z = x (yz ), x 1 = x , 1x = x , x ≤ x .
uxv
31. A decision procedure for RL
Theorem
[Okada and Terui 1999]
An inequality s (x1 , . . . , xn )
≤ t (x , . . . , xn )
1
holds in all
residuated lattices if and only if there is a proof using only the
quasiequations from the previous slide
Moreover it is decidable if such a proof can be found
Use this result to show that x (y
∧ z ) ≤ xy ∧ xz
residuated lattices
but xy
∧ xz ≤ x (y ∧ z )
does not
holds in all
The lattice of subvarieties of (bounded) RL
Draw two diagrams, one with bounded RL at the top, the
other with RL at the top, and the variety of one-element
algebras at the bottom
Then ll in all the varieties from these slides to show how they
are related to each other
Some References
For more hints and background see e.g. some of the following
(available from my website; search for jipsen):
I P. Jipsen and C. Tsinakis, A survey of residuated lattices,
in Ordered Algebraic Structures (J. Martinez, editor),
Kluwer Academic Publishers, Dordrecht, 2002, 1956
I N. Galatos and P. Jipsen, A survey of Generalized Basic
Logic algebras, in Witnessed Years: Essays in Honour of
Petr Hajek", ed. P. Cintula, Z. Hanikova, V. Svejdar,
College Publications, 2009, 305331
I N. Galatos and P. Jipsen, Residuated frames with
applications to decidability, Transactions of the American
Mathematical Society, in press