Download 1.1 radian and degree measure

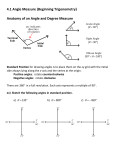
1.1
RADIAN AND DEGREE MEASURE
Copyright © Cengage Learning. All rights reserved.
Angles
The starting position of the ray is the initial side of the
angle, and the position after rotation is the terminal side.
Angle
The endpoint of the ray is the vertex of the angle.
Angles
When the origin is the vertex and the initial side
lies on the positive x-axis, the angle is in standard position.
Angles
Positive angles - counterclockwise
Negative angles - clockwise
Radian Measure
The measure of an angle is determined by the amount of
rotation from the initial side to the terminal side.
One way to measure angles
is in radians.
To define a radian, you can use
a central angle of a circle, one
whose vertex is the center of the
circle.
Arc length = radius when  = 1 radian
Radian Measure
Definition of Radian
One radian is the measure of a central angle θ that intercepts
an arc, s, equal in length to the radius, r, of a circle.
𝑠
𝜃=
𝑟
𝜃 is measured in radians
Since the circumference of a circle is 2 r, it follows that a
central angle of one full revolution corresponds to an arc
length of
s = 2 r.
Radian Measure
Since 2  6.28, there are just over six radius lengths in a
full circle.
Radian Measure
Since one full revolution is 2
Radian Measure
These are additional common angles.
What Quadrant do the following angles lie in?
a)
b)
c)
𝜋
5
11𝜋
8
𝜋
−
4
Radian Measure
Two angles are coterminal if they have the same initial and
terminal sides.
To find coterminal angles, we add or subtract multiples of 2.
A given angle  has infinitely many coterminal angles.
For instance,  =  / 6 is coterminal with
𝜋
+ 2𝑛𝜋
6
where n is an integer.
Example 1 – Sketching and Finding Coterminal Angles
For the positive angle 13 / 6, we can subtract 2 to obtain
a coterminal angle
Example 1 – Sketching and Finding Coterminal Angles
cont’d
For the negative angle –2 / 3, add 2 to obtain a
coterminal angle
Determine two coterminal angles (one positive, one
negative)
Radian Measure
Two positive angles  and  are complementary if their
sum is  / 2.
Two positive angles are supplementary if their sum is .
Complementary angles
Supplementary angles
Degree Measure
A second way to measure angles is in terms of degrees,
denoted by the symbol .
Degree Measure
A full revolution corresponds to 360
Since 2 radians corresponds to one complete revolution
360 = 2 rad or 180 = rad.
Which gives us the following conversions:
Degree Measure
Example 3 – Converting from Degrees to Radians
a.
Multiply by  / 180.
b.
Multiply by  / 180.
c.
Multiply by  / 180.
Applications
The radian measure formula,  = s / r, can be used to
measure arc length along a circle.
Example 5 – Finding Arc Length
A circle has a radius of 4 inches. Find the length of the arc
intercepted by a central angle of 240.
Example 5 – Solution
To use the formula s = r, first convert 240 to radian
measure.
Example 5 – Solution
Since the radius, r = 4 inches
s = r
cont’d
Applications
A sector of a circle is the region bounded by two radii of
the circle and their intercepted arc.
Area of the sector
1
𝐴 = 2 𝑟 2 𝜃 (where 𝜃 is in radians)