Download Diffraction and Interference of EM waves

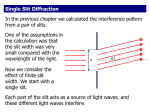
Interference and Diffraction
of EM waves
Maxwell Equations in General Form
Differential form Integral Form
  D  v
 D  dS   v dv
s
 B  0
v
 B  dS  0
s
B
 E  
t

L E  dl   t s B  dS
D
 H  J 
t
D 

H

dl

J


L
s  t   dS
Gauss’s Law for E
field.
Gauss’s Law for H
field. Nonexistence
of monopole
Faraday’s Law
Ampere’s Circuit
Law
Terms
•
•
•
•
E = electric field intensity [V/m]
D = electric field density
H = magnetic field intensity, [A/m]
B = magnetic field density, [Teslas]
Maxwell’s Equations
 v
• Additionally the equation of continuity   J  
t
D
• Maxwell added the term  t to Ampere’s Law so
that it not only works for static conditions but
also for time-varying situations.
• This added term is called the displacement
current density, while J is the conduction current.
Energy (intensity) of electromagnetic
waves
• The frequency of light is very high,
• There is no such detector to measure the electric
field changes,
• We are able only to measure the mean value of the square
root of the electric field,
• our eyes can detect only intensity of light, not phase.
Energy (intensity) of electromagnetic
waves
Poynting vector
Intensity of EM wave
• Light intensity I is a mean velue of square root of the
electric field intensity and is defined in W/m²
• Taking into account the spectral characteristic of human eye,
light intensity is defined in candelas, lumens or lux
Two waves interfering with each other
If two monochromatic waves described as:
will overlap in some plane x=const, then:
Responsible for interference
Two waves interfering with each other
Responsible for interference
For :
>0
constructive interference
=0
<0
destructive interference
The same phases
Constructive interference
The oposite phases
Destructive interference
The key principle: Huygen’s Principle
All points in a wavefront serve as point
sources of spherical secondary waves.
After a time t, the new wavefront will be
the tangent to all the resulting spherical
waves.
Christian Huygens
1629-1695
Huygen’s Principle
For plane waves entering a single slit, the waves emerging from the slit start spreading out,
diffracting
Young’s Double Slit Experiment
For waves entering two slits, the emerging waves interfere and form an interference
(diffraction) pattern
Young experiment in 1801: light is
wave phenomenon
First plane wave through a small slit
yields coherent spherical wave
Then interposed two slits:
interference of two spherical waves
on a screen
Interference
• Phase difference between two waves can change for paths of different lengths
• Each point on the screen is determined by the path length difference DL of the rays
reaching that point
Path Length Difference:
DL  d sin 
Interference
If DL  d sin    integer     bright fringe
Maxima-bright fringes:
d sin   m for m  0,1, 2,
Minima-dark fringes:
d sin    m  12   for m  0,1,2,
 2 
1  1.5 
m

1
dark
fringe
at:


sin
m  2 bright fringe at:   sin 1 



d
d




When the interference is possible
Two sources can produce an interference that is stable over
time, if their light has a phase relationship that does not
change with time: E(t)=E0cos(wt+f).
Coherent sources: Phase f must be well defined and constant
Sunlight is coherent over a short length and time range
Since laser light is produced by cooperative behavior of atoms,
it is coherent of long length and time ranges
Incoherent sources: f jitters randomly in time, no stable
interference occurs
Example of interference
Red laser light (=633nm) goes through two slits d=1cm apart, and produces a
diffraction pattern on a screen L = 55cm away. How far apart are the fringes near
the center?
If the fringes are near the center, we can use
sin  ~ , and then
m=dsin~d => =m/d is the angle for each
maximum (in radians)
D= /d =is the “angular separation”.
The distance between the fringes is then
Dx=LD=L/d=55cm 633nm/1cm=35 mm
For the spacing to be 1mm, we need d~ L/1mm=0.35mm
Example 2
In a double slit experiment, we can measure the wavelength of the light if we
know the distances between the slits and the angular separation of the fringes.
If the separation between the slits is 0.5mm and the first order maximum of the
interference pattern is at an angle of 0.059o from the center of the pattern, what
is the wavelength and color of the light used?
d sin=m =>
=0.5mm sin(0.059o)
= 5.15 x 10-7m=515nm ~ green

Intensity in Double-Slit Interference
E1  E0 sin wt and E2  E0 sin wt  f 
2 d
I  4 I 0 cos2 12 f
f
sin 
E
2
E1

Maxima when: 12 f  m for m  0,1, 2,
 d sin   m for m  0,1, 2,
 f  2m 
2 d

sin 
(maxima)
Minima when: 12 f   m  12    d sin    m  12   for m  0,1, 2,
(minima)
I avg  2 I 0
Example
A double slit experiment has a screen 120cm away from the slits, which are 0.25cm
apart. The slits are illuminated with coherent 600nm light. At what distance above the
central maximum is the average intensity on the screen 75% of the maximum?
I/I0=4cos2f/2 ; I/Imax=cos2f/2 =0.75 => f=2cos–1 (0.75)1/2=60o=/3 rad
f=(2d/)sin => = sin-1(/2d)f0.0022o40 mrad (small!)
y=L48mm
Interferometers
Michelson’s
Mach-Zehnder’s
Ring
Temporal coherence
White light
LED
SLED
LD

Gas laser
He-Ne
D
Measuring the distance with Michelson’s interferometer
Optical coherence tomography
Diffraction
Huygen’s Principle
All points in a wavefront serve as point
sources of spherical secondary waves.
After a time t, the new wavefront will be
the tangent to all the resulting spherical
waves.
Christian Huygens
1629-1695
Huygen’s Principle
For plane waves entering a single slit, the waves emerging from the slit start spreading out,
diffracting
Young’s Double Slit Experiment
For waves entering two slits, the emerging waves interfere and form an interference
(diffraction) pattern
Young experiment in 1801: light is
wave phenomenon
First plane wave through a small slit
yields coherent spherical wave
Then interposed two slits:
interference of two spherical waves
on a screen
Diffraction by a Single Slit:
Locating the Minima
• Path length difference between rays
r1 and r2 is /2
• Two rays out of phase at P1 resulting in
destructive interference
• Path length difference is distance from
starting point of r2 at center of the slit to
point b
• For D>>a, the path length difference
between rays r1 and r2 is (a/2) sin 
Repeat previous analysis for pairs of rays, each separated by a
vertical distance of a/2 at the slit.
Setting path length difference to /2 for each pair of rays, we obtain
the first dark fringes at:
a

sin    a sin   
2
2
(first minimum)
For second minimum, divide slit into 4 zones of equal widths a/4
(separation between pairs of rays). Destructive interference occurs
when the path length difference for each pair is /2.
a

sin    a sin   2
4
2
(second minimum)
Dividing the slit into increasingly larger even numbers of zones, we
can find higher order minima:
a sin   m, for m  1, 2,3
(minima-dark fringes)
Diffraction and the Wave Theory of Light
Diffraction pattern from a single narrow slit.
Side or secondary
maxima
Light
Central
maximum
These patterns cannot be explained
using geometrical optics!
Fresnel Bright Spot.
Light
Bright
spot
Single Slit Diffraction
When light goes through a
narrow slit, it spreads out to
form a diffraction pattern.
Intensity in Single-Slit Diffraction,
Quantitatively
Here we will show that the intensity at the screen due to a single slit
is:
2
 sin  
I    I m 




(36-5)
(1)
1
a
where   f 
sin 
2

In Eq. 1 , minima occur when:
  m ,
for m  1, 2,3
If we put this into Eq. 2 we find:
a
m 
sin  , for m  1, 2,3

or a sin   m , for m  1, 2,3
(minima-dark fringes)
(2)
(36-6)
Diffraction of a laser through a slit
(example)
1.2 cm
Light from a helium-neon laser ( = 633 nm) passes through a narrow slit and is
seen on a screen 2.0 m behind the slit. The first minimum of the diffraction pattern is
observed to be located 1.2 cm from the central maximum.
How wide is the slit?
y1 (0.012 m)
1  
 0.0060 rad
L
(2.00 m)

 (6.33 107 m)
4
a
 

1.06

10
m  0.106 mm
3
sin 1 1 (6.00 10 rad)
Width of a Single-Slit
Diffraction Pattern
-y1 0
y1 y2 y3
w
p L
yp 
;
a
w
2 L
a
p  1, 2,3,
(positions of dark fringes)
(width of diffraction peak from min to min)
1m
1000m
10 m
1m
You are doing 137 mph on I-10 and you pass a little old lady doing 55mph when a cop,
Located 1km away fires his radar gun, which has a 10 cm opening. Can he tell you from
the L.O.L. if the gun Is X-band? What about Laser?
X-band: =10cm
2 L 2  0.1m  1000m
w

 2000m
a
0.1m
Laser-band: =1mm
w
2 L 2  0.000001m  1000m

 0.02m
a
0.1m
Angles of the Secondary Maxima
The diffraction minima
are precisely at the angles
where
sin q = p l/a and a = pp (so
that sin a=0).
However, the
diffraction maxima are not
quite at the angles where
sin q = (p+½) l/a
and a = (p+½)p
(so that |sin a|=1).
l = 633 nm
a = 0.2 mm
1
 sin  
I  I max 

  
2
p
(p+½) /a
Max
1
0.00475
0.00453
2
0.00791
0.00778
3
0.01108
0.01099
4
0.01424
0.01417
5
0.01741
0.01735
2
3
4
5
q (radians)
Diffraction Gratings
A device with N slits (rulings) can be used to manipulate light, such as separate
different wavelengths of light that are contained in a single beam. How does a
diffraction grating affect monochromatic light?
Fig. 36-17
d sin   m for m  0,1, 2
Fig. 36-18
(maxima-lines)
(36-11)
Circular Apertures
Single slit of aperture a
Hole of diameter D
When light passes through a circular aperture instead of a vertical slit, the
diffraction pattern is modified by the 2D geometry. The minima occur at about
1.22/D instead of /a. Otherwise the behavior is the same, including the spread of
the diffraction pattern with decreasing aperture.
The Rayleigh Criterion
The Rayleigh Resolution Criterion
says that the minimum separation to
separate two objects is to have the
diffraction peak of one at the diffraction
minimum of the other, i.e., D  1.22
/D.
Example: The Hubble Space Telescope has a
mirror diameter of 4 m, leading to excellent
resolution of close-lying objects. For light with
wavelength of 500 nm, the angular resolution
of the Hubble is D = 1.53 x 10-7 radians.
Example
A spy satellite in a 200km low-Earth orbit is imaging the Earth in the
visible wavelength of 500nm.
How big a diameter telescope does it need to read a newspaper
over your shoulder from Outer Space?
Example Solution
D  1.22 /D (The smaller the wavelength or the bigger the
telescope opening — the better the angular resolution.)
Letters on a newspaper are about Dx = 10mm apart.
Orbit altitude R = 200km & D is telescope diameter.
R
Formula:
Dx = RD = R(1.22/D)
D = R(1.22/Dx)
= (200x103m)(1.22x500x10–9m)/(10X10–3m)
= 12.2m
Dx
D
Holography
Brief history of holography
• Invented in 1948 by Dennis Gabor – to improve
the resolution in electron microscopy, before the
invention of the laser (this time light sources
were not coherent)
• Leith and Upatnieks (1962) applied laser light to
holography and introduced an important off-axis
technique (the first holographic picture, laser
was necessary to see the picture)
• The pioneer of holography in Poland –
prof. Mieczysław Wolfke (professor from Faculty
of Physics WUT),
Holos - whole, grapho – drawing
•Holography is a method of producing a three-dimensional (3-D) image
of an object. (The three dimensions are height, width, and depth.)
•Later the object can be reconstructed.
•The hologram is actually a recording of the difference between two
beams of coherent light
Can be used as optical store disk, in information processing,
Conventional vs. Holographic picture
• Conventional:
– 2-d version of a 3-d scene
– Photograph lacks depth perception or parallax
– Film sensitive only to radiant energy
– Phase relation (i.e. interference) are lost
Conventional photography
Light
Photographic film:
The intensity is
recorded
Object
Reflected
wave
Conventional photography
Light
Conventional vs. Holographic picture
• Hologram:
– Freezes the intricate wavefront of light that carries all
the visual information of the scene
– To view a hologram, the wavefront is reconstructed
– View what we would have seen if present at the
original scene through the window defined by the
hologram
– Provides depth perception and parallax
Conventional vs. Holographic picture
– Converts phase information into amplitude information
(in-phase - maximum amplitude, out-of-phase – minimum
amplitude)
– Interfere wavefront of light from a scene with a reference
wave
– The hologram is a complex interference pattern of
microscopically spaced fringes
How hologram is made?
• Need a laser, lenses, mirror, photographic film,
and an object
• The laser light is separated into two beams,
reference beam and object beam
• Reference beam enlarged and aimed at a piece
of holographic film
How hologram is made?
• Object beam directed at subject to be recorded
and expanded to illuminate subject,
• Object beam reflects off of object and meets
reference beam at film,
• Produces interference pattern which is recorded,
How hologram is made?
Photographic film.
Interference of reference and
reflected waves is recorded
Reference wave
How hologram is made ?
• Film is developed,
• Hologram illuminated at same angle as
reference beam during original exposure
to reveal holographic image,
Types of holograms
Transmission hologram:
reference and object waves
traverse the film from the
same side
Invented by Benton,
Can be reconstructed
in normal light
Reflection hologram:
reference and object waves
traverse the emulsion from
opposite sides
Applications of holography
•
•
•
•
•
•
Credit cards carry monetary value,
Supermarket scanners,
Optical Computers,
Used in aircraft “heads-up display”,
Art,
Archival Recording of fragile museum
artifacts,
Holography in the future
•
•
•
•
•
•
Medical Purposes
Gaming Systems
Personal Defense
Computers
Artwork
Amusement Park Rides
• Movie production
– Holodeck from Star Trek Holodeck Clip
– Star Wars Chess Game
Summary
• Interference only for coherent light, i.e., with a
phase relationship that is time independent
• Intensity in double-slit interference:
I  4 I 0 cos
2 1
2
f
f
2 d

sin 
• Use Huygens’ Principle to find positions of
diffraction minima of a single slit by subdividing
the aperture
a sin   m, for m  1, 2,3
(minima-dark fringes)
Summary
• Diffraction of light occurs at openings of
the order of the wave length of the light
• Double slit experiment:
Maxima-bright fringes:
d sin   m for m  0,1, 2,
Minima-dark fringes:
d sin    m  12   for m  0,1,2,
• Intensity in double-slit interference:
I  4 I 0 cos2 12 f
f
2 d

sin 
Summary
• To predict the interference pattern of a multi-slit
system, we must combine interference and
diffraction effects.
• Rayleigh’s Criterion for the separability of two
points
• Intensity in single-slit diffraction:
 sin  
I    I m 




2
1
a
where   f 
sin 
(36-5)
2

• Double-slit diffraction:
 sin  
2
I    I m  cos   




2
(double slit)
(36-6)