Download Revision Quadratic Functions

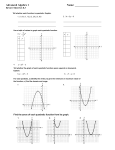
Revision Quadratic Functions
1.
Diagram 1 shows a part of the graph of y = x2.
y
x
0
Diagram 1
Diagrams 2, 3 and 4 show a part of the graph of y = x2 after it has been moved parallel to the
x-axis, or parallel to the y-axis, or parallel to one axis, then the other.
y
y
y
3
3
0
Diagram 2
x
0 2
x
Diagram 3
0 2
x
Diagram 4
Write down the equation of the graph shown in
(a)
Diagram 2;
(b)
Diagram 3;
(c)
Diagram 4.
(Total 4 marks)
Revision Quadratic Functions IB10
MaWa 2013
2.
The graph of the function f (x) = x2 – 2x – 3 is shown in the diagram below.
y
A
Diagram not to scale
0
B
x
C
(a)
Factorize the expression x2 – 2x – 3.
(b)
Write down the coordinates of the points A and B.
(c)
Write down the equation of the axis of symmetry.
(d)
Write down the coordinates of the point C, the vertex of the parabola.
Working:
Answers:
(a) …………………………………………..
(b) ..................................................................
(c) …………………………………………..
(d) ……………………………………..........
(Total 8 marks)
Revision Quadratic Functions IB10
MaWa 2013
3.
The diagram below shows part of the graph of y = ax2 + 4x – 3. The line x = 2 is the axis
of symmetry. M and N are points on the curve, as shown.
y
N
x
0
M
x=2
(a)
Find the value of a.
(b)
Find the coordinates of
(i)
M;
(ii)
N.
Working:
Answers:
(a) …………………………………………..
(b) (i) ……………………………………...
(ii) ……………………………………...
(Total 4 marks)
Revision Quadratic Functions IB10
MaWa 2013
Markscheme Revision Q.
1.
(a)
y = x2 + 3
(A1)
(b)
y = (x – 2)2
(A1)
(c)
y = (x – 2)2 + 3
(A2)
4
[4]
2.
(a)
(x – 3)(x + 1)
Note: Award (A0)(A1) if the signs are reversed.
(A1)(A1) (C2)
(b)
A(1, 0), B(3, 0)
(A1)(A1) (C2)
(c)
x = 1 or x =
(d)
C(1, –4)
( 1 3)
( 2)
= 1 or x =
=1
2
2(1)
Note: Award (A1) for x = and (A1) for 1.
(A1)(A1) (C2)
(A1)(A1) (C2)
[8]
3.
(a)
(b)
b
2a
4
2=
2 a
a = –1
x=
(M1)
(A1)
Note: Answers to (b) must be written as coordinates.
(i)
M(0, –3)
(A1)
(ii)
y = 1 × 22 + 4 × 2 – 3
=1
N is (2,1)
(A1)
[4]
Revision Quadratic Functions IB10
MaWa 2013