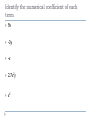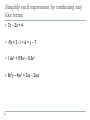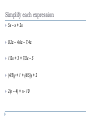Download Class Notes 9-21-2010

Section 1.8
Simplifying Expressions
But, first…

Commutative property: a + b = b + a; a * b = b * a

Associative property: (a + b) + c = a + (b + c)
(a * b) * c = a * (b * c)



Distributive property: a * (b + c) = (a * b) + (a * c)
Also, a * (b – c) = (a * b) – (a * c)
Simplifying expressions





Identifying terms, like terms, and unlike terms
Combining like terms
Simplifying expressions containing parenthesis
Write word phrases as algebraic expressions
Vocabulary: term, numerical coefficient, combining like terms
Identifying Terms, Like Terms, and Unlike
Terms







A term is a number or a product of a number and
variables possibly raised to powers
In other words, a term is pretty much anything
-y is a term: it is the product of -1 and y
2x3 is a term: it is the product of 2 and x3
-5, 3xz2 and 2/y are all terms. 0.8t is a term.
The numerical coefficient of a term is the numerical factor.
The numerical coefficient of -5 is -5
The numerical coefficient of 3xy2 is 3 (not 2, it is a
exponent, and exponents are not factors)
Identify the numerical coefficient of each
term

9x

-3y

-x

2.7x2y

x5
Like terms and unlike terms






Terms with the same variables raised to the exact same
powers are called like terms.
5x and 9x are like terms. The variable for both is x
5x and 9x2 are unlike terms. The variable for 5x is x. The
variable for 9x2 is x2: different powers
6x and 7y are unlike terms: different variables.
5x2y and -4x2y are like terms: same variables and powers
-3ab2 and 5a2b are unlike terms: in the first one, b is
squared, and in the second, a is squared
How about?




Are 9x2y and -6yx2 like terms?
Based on the commutative property, -6yx2 can be written
as -6x2y
Therefore, 9x2y and -6yx2 are like terms
Each variable and its exponent must match exactly, but
the order they are written does not matter
Indicate whether the terms are like terms

6x, -3x

-xy2, -x2y

5ab, (-1/2)ba

2x3yz2, -x3yz3

2zx3yz2, -x3yz3
Combining like terms








Why the big deal about like terms?
In a complicated algebraic expression, like terms can be
combined together to make things simpler
The Distributive property makes this possible
For example, an expression has like terms 6x and 2x
6x + 2x = (6 + 2)x = 8x
Also:
-y2 + 5y2 = (-1 + 5)y2 = 4y2
Simplifying the sum or difference of like terms is called
combining like terms.
Simplify each expression by combining any
like terms

7z – 2z + 4

-9y + 2 -1 + 6 + y – 7

1.6x5 + 0.9x2 – 0.3x5

8x2y – 4yx2 + 2xy – 2xyx
Simplifying expressions containing like
terms










Isn’t simplifying just a matter of removing parenthesis?
(3a + 2) = +1(3a + 2) = +1(3a) + (+1)(2) = 3a + 2
Big deal? Ok, but throw a negative sign in there:
-(3a + 2) = -1(3a + 2) = -1(3a) + (-1)(2) = -3a – 2
In order to remove parenthesis, you have to apply the
Distributed property
-(9x + y – 2z + 6) = -1 * (9x + y – 2z + 6)
Distribute:
-1(9x) + (-1)(y) + (-1)(-2z) + (-1)(6) =
-9x + -y + 2z + -6 =
-9x – y + 2x - 6
Helpful hint: page 71

If a negative “-” sign precedes parenthesis, the sign of each
term within the parenthesis will change when the
parenthesis is removed

-(2x + 1) = -2x – 1

-(x – 2y) = -x + 2y

-(-5x + y – 0.3z) = 5x – y + 0.3z
Use the distributive property to remove the
parenthesis

3(x + 6)

-(-5m + 6n – 2p)

1/3(6x – 9)

14(2x + 6) – 4

10a – 5 – 2(a – 3)
Writing algebraic expressions








Twice a number, plus 6
(2 * x) + 6 = 2x + 6
The difference of a number and 4, divided by 7
(x – 4) ÷ 7
Five plus the sum of a number and 1
5 + (x + 1) = 5 + x + 1 = 6 + x
Four times the sum of a number and 3
4 * (x + 3) = (4 * x) + (4 * 3) = 4x + 12
Write each phrase as an algebraic
expression.

Add -4y + 3 to 6y + 9

Subtract 2x -1 from 3x + 7

Triple a number, decreased by 6

Six times the sum of a number and two
Chapter 1
Review
Vocabulary Check








A mathematical statement that two expressions are equal is
called ___
The ___ of a number is the distance between it and 0 on the
number line
The number in a fraction above the fraction bar is called ___
The number on the bottom of the fraction is the ____
In 23, the 2 is called the ___ and the 3 is the _____
The ___ is the product of a number and variables raised to
powers
The ___ of a term is its numerical factor
Terms with the same variables raised to the same powers are
called ____
Insert <, >, or = in the spaces









8 __ 10
-4 __ - 5
12/2 __ -8
|-7| __ |-8|
|-9| __ -9
-|-1| __ -1
|-14| __ -(-14)
1.2 ___ 1.02
-3/2 ___ -3/4
Translate each statement into symbols

Four is greater than or equal to negative three

Six is not equal to five

0.03 is less than 0.3
{-6, 0, 1, 1½, 3, π, 9.62, √2}

Which are integers?

Which are rational numbers?

Which are irrational numbers?

Which are real numbers?
Simplify (solve) each expression

6 * 32 + 2 * 8

68 – 5 * 23

3(1 + 2 * 5) + 4

8 + 3(2 * 6 – 1)

5[3(2 + 5) – 5]
Translate each word statement to symbols

The difference of twenty and twelve is equal to the
product of two and four

The quotient of nine and two is greater than negative five
Evaluate each when x=6, y=2, & z=8

2x + 3y

x(y + 2z)

(x/y) + (z/2y)

(x2) – 3y2
Decide whether the given number is a
solution to the given equation

7x – 3 = 18; 3

3x2 + 4 = x – 1; 1
Find the additive inverse or opposite to each
number

-9

2/3

|-2|

-|-7|
Solve each problem:










-15 + 4 =
-6 + (-11) =
1/16 + (-1/4) =
-8 + |-3| =
-4.6 + (-9.3) =
6 – 20 =
-3.1 – 8.4 =
-6 – (-11) =
-21 – 16 + 3(8 – 2) =
2 + 3(4) =
Find each multiplicative inverse or
reciprocal

-6

3/5

1¼

0.25

0/12
Simplify (solve) each expression

6(-8)

(-2)(-14)

-18/-6

42/-3

-3(-6)(-2)

(-4)(-3)0(-6)

(3(-2)2 – 5)/-14
Name the property illustrated










-6 + 5 = 5 + (-6)
6*1=6
3(8 – 5) = 3 * 8 + 3 * (-5)
4 + (-4) = 0
2 + (3 + 9) = (2 + 3) + 9
2*8=8*2
(3 * 8) * 4 = 3 * (8 * 4)
4*¼=1
4(8 + 3) = 4(3 + 8)
5(2 + 1) = 5*2 + 5*1
Simplify each expression

5x – x + 2x

0.2z – 4.6z – 7.4z

1/2x + 3 + 7/2x – 5

(4/5)y + 1 + (6/5)y + 2

2(n – 4) + n - 10