Download MPM2D Name:__TEACHER

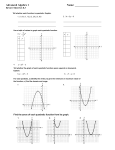
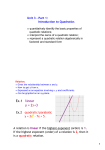
MPM2D
Name:__TEACHER___
Quadratics Review – Day 1 of 2
Quadratic Relations: Vocabulary
Finite differences: are the differences between consecutive values of the dependent variable.
•
First difference: are the values you get when you do the finite differences only once. If they are
all equal, the relation is linear.
•
Second difference: are the values you get when you do the finite differences twice. If they are all
equal, the relation is quadratic.
Quadratic: is the relationship you have when the second differences are constant. It is a second degree
polynomial.
Degree: is the highest exponent that appears in any term of the expanded form of a polynomial.
Properties of Quadratic Relations
A parabola: is the shape of the graph of a quadratic relation.
A vertex: is the point on the graph of a parabola with the greatest y-coordinate (if the graph opens
down) or the least y-coordinate (if the graph opens up). It is usually represented by the coordinates
(h, k).
Optimal value: is the y-coordinate of the vertex when a quadratic relation is used to model a situation.
Maximum: is the greatest y value of the quantity being modeled,
when the parabola opens down.
Maximum is (2,-2)
Minimum: is the smallest y value of the quantity being modeled,
when the parabola opens upwards.
Minimum is (3,2)
Axis of symmetry: is the vertical line that passes through the
vertex. It is the perpendicular bisector of the segments joining any
two points on the parabola that have the same y-coordinates.
Axis of symmetry for top is x=3
Axis of symmetry for bottom is x=2
Zeros or x-intercepts: are the points where the parabola crosses the x axis.
3.4
The Role of the Zeros of a Quadratic Relation
The factored form of a quadratic relation is y = a(x – r)(x – s), provided that a ≠ 0.
a>0
If a > 0, the parabola opens up and has a minimum.
maximum
•
If a < 0, the parabola opens down and has a maximum.
•
minimum
The zeros of a quadratic relation are the solutions to
0 = a ( x − r )( x − s )
a<0
The x-coordinate of the vertex can be found by using the midpoint formula with the values of the zeros.
r+s
x=
2
The y-coordinate of the vertex can be found by substituting the x coordinate into the equation of the
relation.
The value of a can be determined by substituting the coordinates of a point on the curve and the zeros of
the relation.
Ex. If y = (x + 2)(x – 4), determine the zeros and the coordinates of the vertex.
*****Example to be done on the board
Zeros ⇒ 0 = (x + 2)(x – 4)
x + 2 = 0 or x – 4 = 0
x = –2
Vertex ⇒
−2+4
2
x =1
x=
x=4
∴ the zeros are –2 and 4
y = (x + 2)(x - 4)
y = (1 + 3)(1 − 4 )
y = (4 )(− 3)
y = −12
∴ The coordinates of the vertex are (1,−12 )
Ex. What is the equation of a parabola whose zeros are 2 and –3, if it passes through the point A(4,28)?
Zeros mean
y = a(x – 2)(x + 3)
Point A means
28 = a(4 – 2)(4 + 3)
28 = a(2)(7)
28 = 14a
28
=a
14
a=2
∴ Equation is y = 2(x – 2)(x + 3)
Standard Form of a Quadratic Relation
Standard form or expanded form, y = ax2 + bx + c, can be obtained from the factored form by using
the distributive property and then simplifying.
Ex. Expand the expression y = (2x + 3)(3x – 7).
= 2x(3x – 7) + 3(3x – 7)
= 6x2 – 14x + 9x – 21
= 6x2 – 5x – 21
3.8
Factoring Quadratic Expressions
Factoring means writing a quadratic relation that was in the standard form y = ax2 + bx + c and
expressing it as a product of two binomial factors.
Strategy:
1. Find two numbers, n and m, such that:
a. Their product equals the product of a and c: n × m = a × c
b. Their sum equals b: n + m = b
2. Replace the b in the standard form of the equation with n + m
3. Group the first two terms together and the second two terms together and take a common factor
out of each term.
4. Remove the common factor from the two groups of terms.
Ex. Factor
x2 – 14x + 45
Factor
4a2 – 12a + 9
Difference of squares is a special quadratic made up of a square at the beginning minus a square at the
end. It looks like a2x2 – b2 and is factored into (ax + b)(ax – b).
Perfect square is a special quadratic made up of a square at the beginning, a square at the end and two
times the product of their roots in the middle. It looks like a2x2 + 2abx + b2 and is factored into
(ax + b)(ax + b) or (ax + b)2.
Ex. Factor t2 – 8t + 16
Ex. Factor 25x2 – 9