Download The Wave Nature of Light

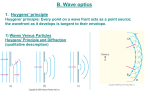
CHAPTER 24
The Wave Nature of Light
http://www.physicsclassroom.com/Class/light/lighttoc.html
Units
•
•
•
•
•
•
•
•
•
•
•
•
Waves Versus Particles; Huygens’ Principle and Diffraction
Huygens’ Principle and the Law of Refraction
Interference – Young’s Double Slit Experiment
The Visible Spectrum and Dispersion
Diffraction by a Single Slit or Disk
Diffraction Grating
The Spectrometer and Spectroscopy
Interference by Thin Films
Michelson Interferometer
Polarization
Liquid Crystal Displays
Scattering of Light by the Atmosphere
What can we say about the nature of light?
Does it travel as a stream of particles away from its source, or does light travel in the form of waves
that spread outward from the source?
In this section we will investigate the wave nature of light.
Huygens, Christiaan (1629-1695)
Dutch physicist who was the leading proponent of the wave
theory of light.
He developed the concept of the wavefront, but could not explain
color.
In 1656, Christiaan Huygens built the world's first pendulum
clock.
Waves Versus Particles; Huygens’ Principle and Diffraction
Huygens’ Principle: Every point on a wave front acts as a point source; the
wavefront as it develops is tangent to their envelope
Huygens principle is useful for analyzing what happens when waves
impinge on an obstacle and the wave fronts are partially interrupted.
1
The bending of waves behind obstacles into the “shadow region” is known as diffraction.
Since diffraction occurs for waves, but not for particles, it is one way for distinguishing the nature of
light.
Waves Versus Particles; Huygens’ Principle and Diffraction
Huygens’ Principle is consistent with diffraction:
The laws of reflection and refraction were well known in Newton’s time. The law of reflection could
not distinguish between the two theories.
The law of refraction is another matter. Consider a ray of light entering a medium where it is bent
toward the normal, as when traveling from air into water.
Huygens’ Principle and the Law of Refraction
This bending can be constructed using Huygens principle if we assume the speed of light is less in
the second medium.
Newton favored a particle theory of light which predicted the opposite result, that the speed of light
would be greater in the second medium.
In 1859 the French physicist Jean Foucault confirmed the wave-theory.
2
Jean Bernard Léon Foucault 1819 -1868) was a French
physicist best known for the invention of the Foucault pendulum, a
device demonstrating the effect of the Earth's rotation. He also
made an early measurement of the speed of light, invented the
gyroscope, and discovered eddy currents.
Huygens’ Principle and the Law of Refraction
Huygens’ Principle can also explain the law of refraction.
As the wavelets propagate from each point, they propagate more slowly in the medium of higher
index of refraction.
This leads to a bend in the wavefront and therefore in the ray.
The frequency of the light does not change, but the wavelength does as it travels into a new
medium.
Highway mirages are due to a
gradually changing index of
refraction in heated air.
Wave Optics
•
•
The wave nature of light is needed to explain various phenomena
– Interference
– Diffraction
– Polarization
The particle nature of light was the basis for ray (geometric) optics
Interference
•
•
Light waves interfere with each other much like mechanical waves do
All interference associated with light waves arises when the electromagnetic fields that
constitute the individual waves combine
3
Conditions for Interference
•
For sustained interference between two sources of light to be observed, there are two
conditions which must be met
– The sources must be coherent
• They must maintain a constant phase with respect to each other
– The waves must have identical wavelengths
Producing Coherent Sources
•
•
•
•
•
•
•
Light from a monochromatic source is allowed to pass through a narrow slit
The light from the single slit is allowed to fall on a screen containing two narrow slits
The first slit is needed to insure the light comes from a tiny region of the source which is
coherent
Old method
Currently, it is much more common to use a laser as a coherent source
The laser produces an intense, coherent, monochromatic beam over a width of several
millimeters
The laser light can be used to illuminate multiple slits directly
Thomas Young (1773-1829)
Young is perhaps best known for his work in physical optics, as
the author of series of research which did much to establish the
wave theory of light, and as the discoverer of the interference of
light. In Young's double-slit experiment, c. 1801, he passed a
beam of light through two parallel slits in an opaque screen,
forming a pattern of alternating light and dark bands on a white
surface beyond. This led Young to reason that light was
composed of waves.
Young’s Double Slit Experiment
•
•
Thomas Young first demonstrated interference in light
waves from two sources in 1801
Light is incident on a screen with a narrow slit, So
•
The light waves emerging from this slit arrive at a
second screen that contains two narrow, parallel slits,
S1 and S2
•
The narrow slits, S1 and S2 act as sources of waves
4
•
The waves emerging from the slits originate from the same wave front and therefore are
always in phase
Young’s Two-Slit Experiment
In this experiment, the original light source need not
be coherent; it becomes so after passing through the
very narrow slits.
If light consists of particles, the final screen should
show two thin stripes, one corresponding to each slit.
However, if light is a wave, each slit serves as a new
source of “wavelets,” as shown, and the final screen
will show the effects of interference. This is called
Huygens’s principle.
Resulting Interference Pattern
•
•
•
•
The light from the two slits form a visible pattern on a screen
The pattern consists of a series of bright and dark parallel bands called fringes
Constructive interference occurs where a bright fringe appears
Destructive interference results in a dark fringe
Fringe Pattern
•
•
•
The fringe pattern formed from a Young’s Double Slit
Experiment would look like this
The bright areas represent constructive interference
The dark areas represent destructive interference
Interference Patterns
•
•
Constructive interference occurs at the center
point
The two waves travel the same distance
– Therefore, they arrive in phase
5
•
•
•
•
•
•
The upper wave has to travel farther than the lower
wave
The upper wave travels one wavelength farther
– Therefore, the waves arrive in phase
A bright fringe occurs
The upper wave travels one-half of a wavelength
farther than the lower wave
The trough of the bottom wave overlaps the crest of
the upper wave
This is destructive interference
– A dark fringe occurs
Young’s Two-Slit Experiment
This diagram illustrates the numbering of the fringes.
6
Between the maxima and the minima, the
interference varies smoothly.
Example 1: Line spacing for double-slit interference.
A screen containing two slits 0.100 mm apart is 1.20 m from the viewing screen. Light of
wavelength   500nm falls on the slits from a distant source. Approximately how far will adjacent
bright interference fringes be on the screen?
Given d  0.100mm  1x104 m,   500 x109 m and L = 1.20m, the first order fringe(m = 1)
occurs at an angle given by
m (1)(500 x109 m)
sin  

 5.00 x103
4
d
1.00 x10 m
This is a very small angle, so we can take sin    ,
with  in radians. The first order fringe will occur a
distance x1 above the center of the screen given by
x1 / L  tan 1  1
So
x1  L1  (1.20m)(5.00 x103 )  6.00mm
The second order fringe (m = 2) will occur at
2
x2  L2  L
 12.0mm
d
Above the center, and so on. Thus the lower order fringes are 6.00 mm apart.
Example 2: Wavelengths from double slit interference.
White light passes through two slits 0.50mm apart, and
an interference pattern is observed on a screen 2.5m
away. The first-order fringe resembles a rainbow with
violet and red light at opposite ends. The violet light falls
about 2.0mm and the red 3.5mm from the center of the
central white fringe.
Estimate the wavelengths for the violet and red light.
For the violet light:
or 400nm. For red light:
d sin  d d x  5.0 x10 m  2.0 x10 m 
7




  4.0 x10 m
m
m mL 
1
 2.5m 
or 700nm
d sin  d d x  5.0 x104 m  3.5 x103 m 
7





  7.0 x10 m
m
m mL 
1
 2.5m 

4
3
7
Interference – Young’s Double-Slit Experiment
Since the position of the maxima (except
the central one) depends on wavelength,
the first- and higher-order fringes contain
a spectrum of colors.
The Visible Spectrum and Dispersion
Wavelengths of visible
light: 400 nm to 750 nm
Shorter wavelengths are
ultraviolet (UV); longer
are infrared (IR).
The index of refraction of a material varies somewhat with
the wavelength of the light.
This variation in refractive index is why a
prism will split visible light into a rainbow of
colors.
Actual rainbows are created by dispersion in
tiny drops of water.
8
Diffraction by a Single Slit or Disk
Light will also diffract around a single slit or obstacle.
The resulting pattern of light and dark stripes is
called a diffraction pattern.
This pattern arises because different points along
a slit create wavelets that interfere with each
other just as a double slit would.
Example 3: Single-slit diffraction maximum.
Light of wavelength 750nm passes through a slit 1.0 x103 mm wide.
How wide is the central maximum (a) in degrees, and (b) in
centimeters, on a screen 20 cm away?
(a) The first minimum occurs at
 7.5x107 m
sin   
 0.75
D 1x106 m
So   49o is the angle between the center and the first minimum.
The angle subtended by the whole central maximum, between the minima above and below the
center, is twice this or 98o
(b) The width of the central maximum is 2x, where tan   x / 20cm . So
2x  2(20cm)(tan 49o )  46cm
Diffraction Grating
•
•
The diffracting grating consists of many equally spaced parallel slits
– A typical grating contains several thousand lines per centimeter
The intensity of the pattern on the screen is the result of the combined effects of
interference and diffraction
9
•
•
•
The condition for maxima is
– d sin θbright = m λ
• m = 0, 1, 2, …
The integer m is the order number of the
diffraction pattern
If the incident radiation contains several
wavelengths, each wavelength deviates
through a specific angle
•
•
•
•
•
All the wavelengths are focused at m = 0
– This is called the zeroth order
maximum
The first order maximum corresponds to m = 1
Note the sharpness of the principle maxima
and the broad range of the dark area
– This is in contrast to the broad, bright
fringes characteristic of the two-slit
interference pattern
The maxima of the diffraction pattern are defined by
10
X-ray diffraction is used to determine crystal structure –
the spacing between crystal planes is close enough to the
wavelength of the X-rays to allow diffraction patterns to
be seen.
A grating spectroscope allows precise determination of
wavelength:
Diffraction can also be observed upon reflection
from narrowly-spaced reflective grooves; the most
familiar example is the recorded side of a CD.
Some insect wings also display reflective
diffraction, especially butterfly wings.
•
•
•
A diffraction grating can be used in a
three-beam method to keep the beam on
a CD on track
The central maximum of the diffraction
pattern is used to read the information on
the CD
The two first-order maxima are used for
steering
Interference by Thin Films
Another way path lengths can differ, and waves interfere, is if the travel through different media.
If there is a very thin film of material – a few wavelengths thick – light will reflect from both the
bottom and the top of the layer, causing interference.
This can be seen in soap bubbles and oil slicks, for example.
11
The wavelength of the light will be different in the oil and the air,
and the reflections at points A and B may or may not involve
reflection.
A similar effect takes place when a shallowly
curved piece of glass is placed on a flat one. When
viewed from above, concentric circles appear that
are called Newton’s rings.
One can also create a thin film of air by creating a wedgeshaped gap between two pieces of glass.
Interference in Reflected Waves
Constructive interference:
Destructive interference:
12
Interference can also occur when light refracts and reflects from
both surfaces of a thin film. This accounts for the colors we see in
oil slicks and soap bubbles.
Now, we have not only path differences and phase changes on
reflection; we also must account for the change in wavelength as
the light travels through the film.
•
Facts to remember
– An electromagnetic wave traveling from a medium of index of refraction n1 toward a
medium of index of refraction n2 undergoes a 180° phase change on reflection when n2 >
n1
–
• There is no phase change in the reflected wave if n2 < n1
The wavelength of light λn in a medium with index of refraction n is λn = λ/n where λ is
the wavelength of light in vacuum
•
•
•
•
•
•
•
•
•
Ray 1 undergoes a phase change of 180° with
respect to the incident ray
Ray 2, which is reflected from the lower surface,
undergoes no phase change with respect to the
incident wave
Ray 2 also travels an additional distance of 2t before
the waves recombine
For constructive interference
– 2nt = (m + ½ ) λ m = 0, 1, 2 …
• This takes into account both the
difference in optical path length for
the two rays and the 180° phase
change
For destruction interference
– 2 n t = m λ m = 0, 1, 2 …
Two factors influence interference
– Possible phase reversals on reflection
– Differences in travel distance
The conditions are valid if the medium above the top surface is the same as the medium
below the bottom surface
If the thin film is between two different media, one of lower index than the film and one of
higher index, the conditions for constructive and destructive interference are reversed
Be sure to include two effects when analyzing the interference pattern from a thin film
– Path length
– Phase change
13
Newton’s Rings
•
•
•
•
Another method for viewing interference is to place a planoconvex lens on top of a flat
glass surface
The air film between the glass surfaces varies in thickness from zero at the point of contact
to some thickness t
A pattern of light and dark rings is observed
– This rings are called Newton’s Rings
– The particle model of light could not explain the origin of the rings
Newton’s Rings can be used to test optical lenses
Problem Solving Strategy with Thin Films
•
•
•
•
Identify the thin film causing the interference
Determine the indices of refraction in the film and the media on either side of it
Determine the number of phase reversals: zero, one or two
The interference is constructive if the path difference is an integral multiple of λ and
destructive if the path difference is an odd half multiple of λ
– The conditions are reversed if one of the waves undergoes a phase change on
reflection
Example 4: Thickness of soap bubble skin.
A soap bubble appears green (  540nm) at the point on
its front surface nearest the viewer. What is the smallest
thickness the soap bubble film could have? Assume
n  1.35 .
t

4n

(540nm)
 100nm
(4)(1.35)
14
Interference in Thin Films, Example
•
•
•
An example of different indices of
refraction
A coating on a solar cell
There are two phase changes
CD’s and Thin Film Interference
•
•
A CD has multiple tracks
– The tracks consist of a sequence of pits of varying length formed in a reflecting
information layer
The pits appear as bumps to the laser beam
– The laser beam shines on the metallic layer through a clear plastic coating
Reading a CD
•
•
•
•
•
As the disk rotates, the laser reflects off the
sequence of bumps and lower areas into a
photodector
– The photodector converts the fluctuating
reflected light intensity into an electrical
string of zeros and ones
The pit depth is made equal to one-quarter of the
wavelength of the light
When the laser beam hits a rising or falling bump
edge, part of the beam reflects from the top of the
bump and part from the lower adjacent area
– This ensures destructive interference and
very low intensity when the reflected
beams combine at the detector
The bump edges are read as ones
The flat bump tops and intervening flat plains are read as zeros
15
DVD’s
•
DVD’s use shorter wavelength lasers
– The track separation, pit depth and minimum pit length are all smaller
– Therefore, the DVD can store about 30 times more information than a CD
Albert A. Michelson1852 -1931
Michelson touched on many departments of physics but, perhaps
due to a special instinct which he appeared to possess, he
excelled in optics. He performed early measurements of the
velocity of light with amazing delicacy and in 1881 he invented his
interferometer for the purpose of discovering the effect of the
Earth's motion on the observed velocity.
Michelson Interferometer
The Michelson interferometer is centered around a beam
splitter, which transmits about half the light hitting it and
reflects the rest. It can be a very sensitive measure of
length.
Polarization
Light is polarized when its electric fields oscillate in a single plane,
rather than in any direction perpendicular to the direction of
propagation.
Polarized light will not be transmitted through a polarized film
whose axis is perpendicular to the polarization direction.
16
When light passes through a polarizer, only
the component parallel to the polarization
axis is transmitted. If the incoming light is
plane-polarized, the outgoing intensity is:
This means that if initially
unpolarized light passes through
crossed polarizer, no light will
get through the second one.
Light is also partially polarized after reflecting from a
nonmetallic surface. At a special angle, called the
polarizing angle or Brewster’s angle, the polarization
is 100%.
Liquid Crystal Displays (LCD)
Liquid crystals are
unpolarized in the
absence of an external
voltage, and will easily
transmit light. When an
external voltage is applied,
the crystals become
polarized and no longer
transmit; they appear
dark.
Liquid crystals can be
found in many familiar
applications, such as
calculators and digital
watches.
17
Color LCD displays are more complicated; each pixel has three subpixels to provide the different
colors. A source of light is behind the display (unlike calculators and watches, which use ambient
light). The pixels must be able to make finer adjustments than just on and off to provide a clear
image.
•
•
Rotation of a
polarized light beam
by a liquid crystal
when the applied
voltage is zero
Light passes through
the polarizer on the
right and is reflected
back to the observer,
who sees the
segment as being
bright
•
•
•
•
When a voltage is
applied, the liquid
crystal does not
rotate the plane of
polarization
The light is absorbed
by the polarizer on
the right and none is
reflected back to the
observer
The segment is dark
Changing the applied voltage in a precise pattern can
– Tick off the seconds on a watch
– Display a letter on a computer display
18
CHAPTER 24
WAVE NATURE OF LIGHT
CONCEPTS
1. For a thin spherical lens, the focal length of red light compared to
the focal length of blue light is greater.
2. The wave theory of light is attributed to Christian Huygens.
3. The particle theory of light is attributed to Isaac Newton.
4. The principle responsible for light spreading as it passes through a narrow slit is diffraction.
19
5. The principle responsible for alternting light
and dark bands when light passes through
two or more narrow slits is called
interference.
6. The principle responsible for the fact that certain sunglasses can reduce glare from
refected surfaces is polarization.
7. The principle on which fiber optics is based is total internal reflection.
8. The principle which allows a rainbow to form is dispersion.
9. The principle on which lenses work is refraction.
10. The principle which explains why a prism separates white light into different colors is
dispersion.
11. Objects under water appear closer than they are because of refraction.
12. All points on a given wave front have the same phase.
13. Rays are always perpendicular to wave fronts.
14. The spacing between adjacent wave fronts is one-half waavelength.
15. When a light wave enters into a medium of different optical density its speed and
wavelength change.
16. When a beam of light (wavelength = 590 nm), originally traveling in air, enters a piece of
glass (index of refraction 1.50), its frequency is unaffected.
17. When a beam of light (wavelength = 590 nm), originally traveling in air, enters a piece of
glass (index of refraction 1.50), its wavelength is reduced to 2/3 its original value.
18. The index of refraction of diamond is 2.42. This means that a given frequency of light
travels 2.42 times faster in vacuum than it does in diamond.
19. When a ray of light passes obliquely from one medium to another, the direction of travel,
wavelength and speed changes.
20
20. White light is a mixture of all frequencies.
21. You can only see a rainbow if the sun is behind you.
22. The color on the outer edge of the primary rainbow is red.
23. Two light sources are said to be coherent if they are of the same frequency, and maintain
a constant phase difference.
24. Ina double slit experiment, it is observed that the distance between adjacent maxima on a
remote screen is 1 cm. The distance between adjacent maxima is increased to 2 cm when
the slit separation is cut in half.
25. At the first maxima on either side of the central bright spot in a double slit experiment, light
from each opening arrives in phase.
26. At the first maxima on either side of the central bright spot in a double slit experiment, light
from one opening travels two wavelengths of light farther than light from the other opening.
27. The colors on an oil slick are caused by reflection and interference.
28. When a beam of light, which is traveling in glass, strikes an air boundary, there is no phase
change in the reflected beam.
29. When a beam of light, which is traveling in air, is reflected by a glass surface, there is a
180o phase change in the reflected beam.
30. A soap film is being viewed in white light. As the film becomes very much thinner than the
wavelength of blue light, the film appears black because it reflects no visible light.
31. In terms of the wavelength of light in soapy water, the minimum thickness of soap film that
will reflect a given wavelength of light is one-fourth wavelength.
32. After a rain, one sometimes sees brightly colored oil slicks on the road. These are due to
interference effects.
33. Consider two different gratings; one has 4000 lines per cm and the other one has 6000
lines per cm. The 6000-line grating produces the greater dispersion.
34. For a beam of light, the direction of polarization is defined as the direction of the electric
field’s vibration.
35. The polarization of sunlight is greatest at both sunrise and sunset.
PHYSICSINMOTION
21