Download protostars and pre-main-sequence evolution.key

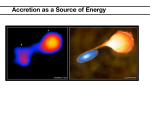
Chapter 5
Protostars and pre-mainsequence evolutiona
Definition
• A protostar is the object that forms in the center of a
collapsing cloud, before it becomes (optically) visible.
• A pre-main sequence star is optically visible and has
no central hydrogen burning
• As soon as hydrogen burning starts, the object is
called a star (main sequence star).
Timescales
 3π 1/2
t ff = 

 32Gρ 
Free fall timescale
Kelvin-Helmholtz timescale
W GM *2
=
= 3×10 7 yr for the Sun
L R* L€*
M
Accretion timescale
tacc = core
M˙
tKH =
€
t ff << tKH ,
€
€
t ff << tacc
2 cases for timescales:
tKH < tacc
• Star evolved toward main sequence, contraction is
slow, luminosity generated by contraction
€
tKH > tacc
• Stellar interior does not adjust thermally as new matter
get piled onto the top. Luminosity is generated at the
surface by accretion shocka
€
First core
• Ambipolar diffusion is faster in central
dense region (why??), so this is where
the protostars forms as slow contraction.
central temperature
• Central lump becomes opaque to its
own radiation: Isothermal approximation
breaks down, the temperature rises
steadily.
• New matter settle on the core which is
growing until it is 5AU and 5§10-2Msun
• Dissociation of H2 acts as a thermostat
Virial
theorem:
T≈

 R −1
µ GM
M
= 850K


−2
3R R
 5 ×10 M o  5AU 
Accretion Luminosity
€
• Gas falling onto the protostar heats the surface and
radiates directly. This additional luminosity is called
accretion luminosity Lacc
Lacc =

 M *  R* −1
GM * M˙
M˙
= 61Lo  −5



R*
10 M o / yr 1M o  5Ro 
• Throughout the main accretion phase, Lacc accounts
for most of Lrad.
€
• Other definition for protostar: Mass gaining star whose
luminosity is dominated by accretion luminosity.
Dust envelope and opacity gap
• Dust is destroyed at
1500 K.
• A gap forms
between the
protostar surface
and the location of
the 1500K
boundary.
• Dust photosphere is
visible in IR
observations.
Stellar structure equations I
Write hydrostatic end energy equations
as function of Mr
∂r
1
=
∂M r 4 πr 2 ρ
mass conservation
∂P
GM ρ
∂P
GM r
= − 2r ⇒
=−
∂r
r
∂M r
4 πr 4
€
ρ
P=
kT
equation of state
µm p
Note: more complicated than in cloud
hydrostatic equil.
because of dissociation, ionization
€
€
Stellar structure equations II
radiative energy transport
T3
∂T
3κLint
=−
∂M r
256π 2σ r 4
∂Lint
∂s
=ε −T
∂M r
∂t
Energy production
€
specific entropy s.
For simple monoatomic gas given by
€
€
k T 3/2 
s = ln
+ s
µ  ρ  0
Stellar structure equations III
Boundary conditions
from ram pressure infall
r(0) = 0
Lint (0) = 0
P(M * ) =
1/2
M˙  2GM * 


4 π  R*5 
L* = Lacc + Lint (M * )
Final ingredient: Mass accretion rate, from collapse model.
Equations are solved €
using guessed central values for P, T,
iterate until match with outer boundary conditions.
Mass radius relation
• Independent of initial
condition after doubling of
mass
The onset of convection
• Stars produced by accretion are stable against
convection, because the strengthening of the accretion
shock leads to an increasing entropy profile.
• Radiation can carry a limited amount of luminosity
Lcrit =
64 πGM rσT 3 ∂T 
 
 ∂P s
3κ
• Once nuclear burning sets in, convection starts and
leads to a constant specific entropy object.
€
Hayashi’s theory (1961)
• Minimum surface temperature 4000-5000K
– due to extremely strong dependence of the H- opacity on
temperature
• fully convective star
– Star is fully convective, polytrope with index n=3/2
p = Kρ γ = Kρ (n+1)/n = Kρ 5 / 3
T ∝ p/ρ
p = KT n+1 = KT 5 /2
€
Forbidden regime for young stars
• Star is fully convective, polytrope with index n=3/2
Deuterium burning
LD = M˙ δ
10 6 K : 2 D + 1H → 3He + γ
10 7 K : H burning via pp chain or CNO cycle
€
• Deuterium luminosity is proportional to accretion rate
and acts as a thermostat while star is fully convective.
• But:
Lrad
€
 M * 11/2  R* −1/2
= Lo    
 M o   Ro 
Deuterium burning
log Teff
Effect of the Deuterium thermostat on the
zero D
Observation of birthline in Taurus/Aurigae
• Open circles are
classical T Tauri stars
(with disks and
accretion
• Filled circles are
“weak-line” T Tauri
stars, accretion has
stopped, these are
older.