Download Proving the Alternate Interior Angles Theorem

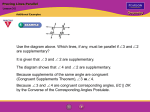
Primary Type: Formative Assessment
Status: Published
This is a resource from CPALMS (www.cpalms.org) where all educators go for bright ideas!
Resource ID#: 56789
Proving the Alternate Interior Angles Theorem
In a diagram involving two parallel lines and a transversal, students are asked to use rigid motion to prove that alternate interior angles are
congruent.
Subject(s): Mathematics
Grade Level(s): 9, 10, 11, 12
Intended Audience: Educators
Freely Available: Yes
Keywords: MFAS, congruent, alternate interior angles, Parallel Postulate, rigid motion
Resource Collection: MFAS Formative Assessments
ATTACHMENTS
MFAS_ProvingTheAlternateInteriorAnglesTheorem.docx
FORMATIVE ASSESSMENT TASK
Instructions for Implementing the Task
This task can be implemented individually, with small groups, or with the whole class.
1. The teacher asks the student to complete the problems on the Proving the Alternate Interior Angles Theorem worksheet.
2. The teacher asks follow-up questions, as needed.
Note: This task assumes that no other special angle pairs in the context of parallel lines and a transversal have yet been shown congruent. The rubrics are written with the
assumption that the congruence of alternate interior angles is the first of the special angle pairs to be shown congruent and that the instructional approach taken relies on
rigid motion. The following theorem is needed in the proof and should be established first: Given line l and point A not on line l, the image of line l under a 180° rotation
about point A is a line parallel to l.
TASK RUBRIC
Getting Started
Misconception/Error
The student is unable to use rigid motion to prove alternate interior angles are congruent.
Examples of Student Work at this Level
The student attempts a proof that does not rely on rigid motion. The student may engage in circular reasoning by using the statement to be proven in the proof. The
student may also use a theorem that has not yet been established such as the Corresponding Angles Theorem (i.e., if two parallel lines are intersected by a transversal,
page 1 of 3 then corresponding angles are congruent).
Questions Eliciting Thinking
What does it mean to use rigid motion to prove these angles are congruent? What are some examples of rigid motion?
Can you use a theorem in its own proof? Would that be convincing?
Have we established yet that corresponding angles are congruent in diagrams such as this?
Instructional Implications
Review the definition of a rotation, properties of rotations, and the theorem that states that the image of a line under a 180° rotation is parallel to the original line. Also
review the Parallel Postulate (i.e., there is exactly one line parallel to a given line through a given point not on the line) and the theorem that states that if two lines are
each parallel to the same line, then the two lines are parallel to each other. Guide the student through a proof of the Alternate Interior Angles Theorem using rigid motion.
Give the student a diagram such as the one used in this task, and ask the student to locate point M, the midpoint of
. Then allow the student to use tracing paper to
perform the indicated 180° rotation. Encourage the student to refer to the diagram and guide the student through the remaining steps of the proof justifying each
statement. Ask the student to explain (1) why it was important to use the midpoint of
as the center of rotation and a rotation of measure 180° about this point, (2)
how the Parallel Postulate was used, and (3) what properties of rigid motion were necessary.
Provide additional opportunities to use rigid motion to prove angles are congruent in diagrams involving lines and angles.
Moving Forward
Misconception/Error
The student attempts to use rigid motion but is unable to write a complete and convincing proof.
Examples of Student Work at this Level
The student:
Informally describes a reflection followed by a translation that maps one angle to the other.
Suggests a 180° rotation of the transversal will show the angles align.
Says that since rigid motion preserves angle measure, the angles must be congruent.
Questions Eliciting Thinking
What if lines a and b were not parallel? Would the sequence of rigid motions you described map
to
?
Why is the assumption that line a is parallel to line b important?
Can you describe this rotation in more detail? About which point are you rotating?
Instructional Implications
Provide feedback to the student and explain why the proof he or she wrote is not convincing. For example, if the student describes a reflection followed by a translation,
have the student perform this sequence of transformations using the given diagram as well as one in which lines a and b are not parallel. Explain the importance of using the
given assumptions in the proof.
Review the theorem that states that the image of a line under a 180° rotation is parallel to the original line, the Parallel Postulate (i.e., there is exactly one line parallel to a
given line through a point not on the given line), and the theorem that states that if two lines are each parallel to the same line, then the two lines are parallel to each
other. Guide the student through a proof of the Alternate Interior Angles Theorem using rigid motion. Give the student a diagram such as the one used in this task, and ask
the student to locate point M, the midpoint of
. Then allow the student to use tracing paper to perform the indicated 180° rotation. Encourage the student to refer to
the diagram and guide the student through the remaining steps of the proof justifying each statement. Ask the student to explain (1) why it was important to use the
midpoint of
as the center of rotation and a rotation of measure 180° about this point, (2) how the Parallel Postulate was used, and (3) what properties of rigid motion
were necessary.
Provide additional opportunities to use rigid motion to prove angles are congruent in diagrams involving lines and angles.
Almost There
Misconception/Error
The student uses rigid motion to develop a convincing argument but leaves out some detail.
Examples of Student Work at this Level
The student writes an essentially correct proof but:
Assumes, rather than proves, that the image of line b is parallel to line a.
Never uses the definition of a midpoint to justify that the image of point B coincides with point A.
Neglects to be explicit about the use of properties of rigid motion in the proof.
Questions Eliciting Thinking
How do you know the image of line b is parallel to line a?
How do you know that the image of point B coincides with point A?
You showed how to map the image of
to
but what property of rigid motion assures us that
is congruent to its image after this mapping?
Instructional Implications
Provide feedback to the student concerning any errors or omissions and allow the student to revise his or her proof. Emphasize the need to justify each statement using
the given assumptions, properties of rigid motion, and previously established theorems. Provide additional opportunities to use rigid motion to prove angles are congruent in
diagrams involving lines and angles.
page 2 of 3 Got It
Misconception/Error
The student provides complete and correct responses to all components of the task.
Examples of Student Work at this Level
The student uses rigid motion to prove that alternate interior angles,
Let M be the midpoint of
and
, are congruent. For example, the student writes:
. Consider a 180° rotation about point M. By a previously proven theorem, line b', the image of line b under this rotation, is parallel to line b.
Since by assumption, a is parallel to b, then by a previously proven theorem, a is parallel to b'. Since AM = MB, by definition of a midpoint, and because rotations preserve
distance, point B is mapped to point A so that line b' contains point A. Since both line b' and line a contain point A and are parallel to line b, by the Parallel Postulate, line b'
coincides with line a. Since line b' coincides with line a and the image of point B coincides with point A, the image of
coincides with
. Since rotations preserve the degree measure of an angle,
coincides with
so that the image of
.
Questions Eliciting Thinking
Was it necessary that point M be the midpoint of
? Why?
What properties of rigid motion did you rely on in this proof?
Instructional Implications
Define corresponding angles and ask the student to use the Alternate Interior Angles Theorem to prove that they are congruent.
ACCOMMODATIONS & RECOMMENDATIONS
Special Materials Needed:
Proving the Alternate Interior Angles Theorem worksheet
SOURCE AND ACCESS INFORMATION
Contributed by: MFAS FCRSTEM
Name of Author/Source: MFAS FCRSTEM
District/Organization of Contributor(s): Okaloosa
Is this Resource freely Available? Yes
Access Privileges: Public
License: CPALMS License - no distribution - non commercial
Related Standards
Name
MAFS.912.G-CO.3.9:
Description
Prove theorems about lines and angles; use theorems about lines and angles to solve problems. Theorems include:
vertical angles are congruent; when a transversal crosses parallel lines, alternate interior angles are congruent and
corresponding angles are congruent; points on a perpendicular bisector of a line segment are exactly those equidistant
from the segment’s endpoints.
page 3 of 3