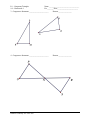
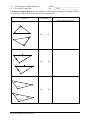
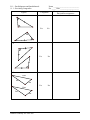
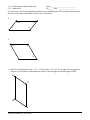
* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
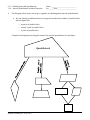
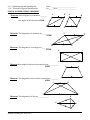
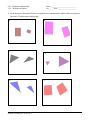
Download Geometry Quarter 2
Noether's theorem wikipedia , lookup
Cartesian coordinate system wikipedia , lookup
Golden ratio wikipedia , lookup
Euler angles wikipedia , lookup
Technical drawing wikipedia , lookup
Multilateration wikipedia , lookup
Reuleaux triangle wikipedia , lookup
Trigonometric functions wikipedia , lookup
Rational trigonometry wikipedia , lookup
Geometrization conjecture wikipedia , lookup
Line (geometry) wikipedia , lookup
History of trigonometry wikipedia , lookup
History of geometry wikipedia , lookup
Integer triangle wikipedia , lookup
Geometry Quarter2 Ø ExploringTriangles Ø CongruentTriangles Ø PerpendicularLinesand Triangles Ø Parallelogramsand Quadrilaterals Ø DilationsandSimilarity Ø SimilarTriangles Ø Similarityand Proportionality MotherNaturelovesmath,too! Constructaseriesofsquareswithlengths thatfollowthenumbersintheFibonacci sequence(1,1,2,3,5,8,13,21,…)and thentraceacurvethroughopposite verticesofeachsquare. Thisformsa“Fibonaccispiral” (#fibonaccispiral).Manyexamplesofthe Fibonaccispiralcanbeseeninnature, includinginthechambersofanautilusshell. Noticehowthepetalsofarosespirals? Howcoolisthat? Table of Contents L8-8.1 Introduction 1 L8-8.2 Angle and Side Relationship 3 L8-8.3 Exterior Angle Theorem 11 L8-8.4 Triangle Inequality Theorem 15 L9-9.1 Introduction 19 L9-9.2 Determining Congruence 21 L9-9.3 Identifying Congruent Triangles 29 L9-9.4 Homework 1 31 L9-9.5 Proving Congruent Triangles 35 L9-9.6 Homework 2 37 Perpendicular Lines & Triangles L10-10.1 Construction Warmup 39 L10-10.2 Grandma’s Roof 40 L10-10.3 Homework 47 L10-10.4 Attic Access Revisited 51 L10-10.5 Finding the Center of Revolution 53 L11-11.1 Revisiting Congruence 57 L11-11.2 Properties of Parallelograms 59 L11-11.3 Homework 65 L11-11.4 Parallelogram Angle Proofs 67 L11-11.5 Homework 71 L11-11.6 Diagonals of Parallelograms 73 L11-11.7 Congruent Quadrilaterals 77 L11-11.8 Special Quadrilaterals and their Properties 81 L11-11.9 Theorems of Special Quadrilaterals 87 Lesson 9: Congruent Triangles Lesson 8: Title Exploring Triangles Lesson Lesson 10: Quarter 2 Lesson 11: Parallelograms and Quadrilaterals Geometry Page i Table of Contents Lesson 14: Similarity and Proportionality Lesson 13: Similar Triangles Lesson 12: Dilations and Similarity Geometry Quarter 1 Lesson Title Page L12-12.1 Refresher on Ratios 93 L12-12.2 Grandma’s Gazebo 95 L12-12.3 Dilations 103 L12-12.4 Introduction to Similarity 109 L12-12.5 Homework 113 L13-13.1 Looking Ahead: Using Similar Triangles to Solve Problems 115 L13-13.2 Characteristics of Similar Triangles 117 L13-13.3 Similarity and Proportion 119 L13-13.4 Homework 123 L13-13.5 Theorems About Similar Triangles 125 L13-13.6 Homework 131 L13-13.7 The Geometric Mean 133 L14-14.1 Construction Warm-up 141 L14-14.2 The Altitude and Mean 143 L14-14.3 The Mid-segment Theorem 145 L14-14.4 Homework 149 L14-14.5 Using Proportionality to Find Coordinates 151 L14-14.6 Parallel Lines in Triangles (Warm-up) 157 L14-14.7 Parallel Lines in Triangles 159 L14-14.8 Medians and Altitudes in Similar Triangles 163 L14-14.9 Homework 169 ii L8 – Exploring Triangles 8.1 – Introduction Name___________________________ Per________ Date_________________ Inequality Review 1. Write inequalities to model the sentences below. a. Keanu is older than Justin. Justin is older than David. b. Mary has less money than Keani. Keani has less money than Nani. c. In the golf match, the Vulcans shot fewer strokes than the Warriors who shot fewer strokes than the Trojans. d. Walmart has more employees than McDonald’s who has more employees than Burger King. e. 𝐴𝐵is longer than 𝐶𝐷, which is longer than 𝐸𝐹. 2. Using the above inequalities, express the following relationships with another inequality. a. The relationship between Keanu and David. b. The relationship between Mary’s and Nani’s money. c. The relationship between the Vulcans’ and Trojans’ golf scores. d. The relationship between the number of employees in Walmart and Burger King. e. The relationship between 𝐴𝐵 and 𝐸𝐹. 3. If Keanu is older than Justin, but Justin is older than Nathan, what can we conclude about the relationship between Keanu and Nathan? Explain your reasoning. HIDOE Geometry SY 2016-2017 1 HIDOE Geometry SY 2016-2017 2 L8 – Exploring Triangles 8.2 – Angle and Side Relationship Name___________________________ Per________ Date_________________ Investigating Roof Designs Below are two possible designs for the roof on Grandma’s house. Uncle Bobby wants to know more about the designs and realizes the designs lack measurements. He needs to know if the roofs are too steep to build or too flat (could leak). Using your ruler and protractor, measure each angle and each side. Record the measurements on the picture. Roof Design #1 Roof Design #2 Based on your prior knowledge, what is the sum of the interior angles of a triangle? Do your measurements agree with that sum? Compare the length of a side to the measure of the angle opposite that side. Do you notice any patterns? (hint: look at the sizes of the sides and angles compared with the other sides and angles in the triangle). HIDOE Geometry SY 2016-2017 3 L8 – Exploring Triangles 8.2 – Angle and Side Relationship Name___________________________ Per________ Date_________________ Investigating Your Patterns Measure the sides and the angles of the four triangles below. Label each on the sketch. Classify each triangle two ways: A. By its Angle Name as Acute, Obtuse, or Right. B. By its Sides Name as Scalene,Isosceles,orEquilateral. 1. Angle Name ___________________ Side Name ____________________ 2. Angle Name ___________________ Side Name ____________________ 3. Angle Name ___________________ Side Name ____________________ HIDOE Geometry SY 2016-2017 4 L8 – Exploring Triangles 8.2 – Angle and Side Relationship 4. Name___________________________ Per________ Date_________________ Angle Name ___________________ Side Name ____________________ Based on your measurements, did the pattern you discovered in Grandma’s roof designs hold with these triangles? Trace the triangles onto patty paper. Rip off each vertex (keep each vertex with the other two vertices of the same triangle), and arrange the vertices so that they are adjacent (i.e. so that one ray of the first coincides with one ray of the second, and the remaining ray of the second coincides with one ray of the third). What do you notice? Make a conjecture about the sum of the angles. HIDOE Geometry SY 2016-2017 5 L8 – Exploring Triangles 8.2 – Angle and Side Relationship Name___________________________ Per________ Date_________________ Sum of the Measures of the Interior Angles of a Triangle Based on your measurements, complete the statement: The sum of the measures of the interior angles of a triangle is __________________. (#THM) Let’s prove it. Use the diagram below. Given: ∆𝐴𝐵𝐶 and line m ∥ 𝐶𝐴 Prove: 𝑚∠1 + 𝑚∠2 + 𝑚∠3 = 180° Statement HIDOE Geometry SY 2016-2017 Reason 6 L8 – Exploring Triangles 8.2 – Angle and Side Relationship Name___________________________ Per________ Date_________________ Using Sum of the Interior Angles Theorem Fill in any missing interior angle measures. 1. 2. 58.3° 54° 47° 89.5° 3. 130.8° 37.32° 4. Solve for x in each of the triangles. (Hint: the sum of the measures of the interior angles equals 180. Set up an equation to show that sum and solve for x.) (𝑥)° (𝑥 + 12)° (3𝑥 + 32)° (𝑥 − 4)° 50° HIDOE Geometry SY 2016-2017 7 L8 – Exploring Triangles 8.2 – Angle and Side Relationship Name___________________________ Per________ Date_________________ Proof of the Longer Side Inequality Theorem State your conjecture from the previous work regarding the lengths of the sides and the measures of the angles here. In more formal language, (#THM) we can say, One side of a triangle is longer than another side of a triangle if and only if the measure of the angle opposite the longer side is greater than the angle opposite the shorter side. Now let’s prove it. Given:∆𝐴𝐵𝐶 ∶ 𝐴𝐶 > 𝐴𝐵 ???? ∶ ???? Construct:𝐵𝐷 𝐴𝐷 ≅ ???? 𝐴𝐵 Prove:𝑚∠𝐴𝐵𝐶 > 𝑚∠𝐶 A D B C Statement 1. DABC; AC > AB 2. BD : AD @ AB HIDOE Geometry SY 2016-2017 Reason 1. Given 2. Congruent segment construction 8 L8 – Exploring Triangles 8.2 – Angle and Side Relationship Name___________________________ Per________ Date_________________ Using the Longer Side Inequality Based on the longer side inequality theorem, list the sides of the triangles in order of longest to shortest. 1. 2. A E 126° 36° 70° D F 67° C B Based on the longer side inequality, list the angles in order of size from largest to smallest. A 3. 4. 7.49 5.93 5.65 D 5.79 C 6.04 B F 6.19 E For all the above problems, explain your reasoning for listing the sides or angles in the order that you did. HIDOE Geometry SY 2016-2017 9 HIDOE Geometry SY 2016-2017 10 L8 – Exploring Triangles 8.3 – Exterior Angle Theorem Name_____________________________ Per________ Date_________________ Exterior Angle Theorem Grandma has a side job for you. She wants her chicken coop repaired. We need to start with a repair to the area where the roof meets the front wall. We need to build a support that is the exact same angle as that. It’s too dangerous to measure that angle directly, but luckily, we know the angle between the roof and ceiling and the angle between the ceiling and front wall. Below is a sketch of the chicken coop and the angles that we know. Below is a sketch of a side view Grandma’s old chicken coop. Angleweneedtomeasure Roof 23° Ceiling 90° Frontwall Floor How can we deduce the measure of the angle we are looking for without actually measuring it? (Complete the next activity to find out.) HIDOE Geometry SY 2016-2017 11 L8 – Exploring Triangles 8.3 – Exterior Angle Theorem Name_____________________________ Per________ Date_________________ The diagram below shows exterior angles, adjacent interior angles, and remote interior angles of a triangle. (#VOC) Remote Interior Angle Exterior Angle Adjacent Interior Angle Measure the exterior angles and remote interior angles on the triangles below. Compare your measurements with your classmates. Based on your measurements, describe any patterns you see between the exterior angle and the remote interior angles. HIDOE Geometry SY 2016-2017 12 L8 – Exploring Triangles 8.3 – Exterior Angle Theorem Name_____________________________ Per________ Date_________________ Exterior Angle Theorem (#THM) The exterior angle theorem states that given a triangle and an exterior angle of that triangle, the measure of the exterior angle is equal to the sum of the measures of the two remote interior angles. Remote Interior Angle Exterior Angle Adjacent Interior Angle Use the figure below to prove the exterior angle theorem. A Given: ∆𝐴𝐵𝐶 and exterior angle ∠𝐷𝐶𝐴 Prove: 𝑚∠𝐷𝐶𝐴 = 𝑚∠𝐴 + 𝑚∠𝐵 B Statement HIDOE Geometry SY 2016-2017 C D Reason 13 HIDOE Geometry SY 2016-2017 14 L8 – Exploring Triangles 8.4 – Triangle Inequality Theorem Name_____________________________ Per________ Date_________________ Creating Triangles In this exercise, you will create a triangle with straws (or pieces of spaghetti). You should have 6 different length straws of 5, 6, 8, 12, 13, 14 cm. Create triangles with the indicated lengths. Record whether your triangles are acute, obtuse, or right. If it is not possible to create a triangle with the straws, write “not possible”. All the measurements are in cm and the sides are labeled a, b, and c. 1. a = 5, b = 12, c = 13 2. a = 5, b = 6, c = 8 3. a = 5, b = 6, c = 12 4. a = 5, b = 8, c = 12 5. a = 5, b = 8, c = 13 6. a = 8, b = 12, c = 14 7. a = 6, b = 8, c = 13 8. a = 6, b = 8, c = 14 List the side lengths of the triangles below in the possible or not possible categories. Possible Not Possible Do you notice any patterns? In other words, why were some combinations not possible? HIDOE Geometry SY 2016-2017 15 L8 – Exploring Triangles 8.4 – Triangle Inequality Theorem Name_____________________________ Per________ Date_________________ Possible or Not? 1. Determine whether you could construct a triangle given the following combinations of side lengths. If “not possible”, explain your reasoning. a) 4, 5, 9 cm b) 4, 6, 9 cm c) 7, 13, 8 cm d) 9, 3, 5 cm 2. Dezmond decides to build a triangular garden. He has three extra 2"x4" boards lying in his shed. He measures the board lengths and finds them to be 4, 10, and 3 ft. a. Will he be able to build a triangular garden without adjusting his boards? Explain your reasoning. b. If Dezmond is only comfortable in working in whole number measurements, what does he have to do to ensure that he is able to build a triangular garden with those boards? 3. Gabby saw Dezmond’s triangular boxes and wants to build her own. She has 6 boards, but no way to cut the boards. Her boards have lengths of 4 ft, 7 ft, 2 ft, 3.5 ft, 6 ft, and 5 ft. What combinations of boards will not work to build a triangle? Explain your reasoning. The Triangle Inequality Theorem (#THM): If a, b, and c represent the side lengths of a triangle, then each must be less than the sum of the other two. HIDOE Geometry SY 2016-2017 16 L8 – Exploring Triangles 8.4 – Triangle Inequality Theorem Name_____________________________ Per________ Date_________________ Shortest Way – As the Nene Flies Below is a diagram of two villages on a map, with a lake between the two villages. Young’sVillage Takahashi’sVillage The dotted line represents the flight of a nene between the two villages, and the solid line represents the walking trail. Using the triangle inequality theorem, explain why the flight of the nene is shorter than the walking trail. Extension: Justify the statement “the shortest distance between two points is a straight line.” HIDOE Geometry SY 2016-2017 17 HIDOE Geometry SY 2016-2017 18 L9 – Congruent Triangles 9.1 – Introduction Name ________________________________ Per _______ Date _______________________ How Do We Compare? Using patty paper, compare the lengths and angles of the following triangle pairs. Record what is the same for each pair and what is different. 1. What is common? What is different? Is there a rigid motion that shows they are congruent? 2. What is common? What is different? Is there a rigid motion that shows they are congruent? HIDOE Geometry SY 2016-2017 19 L9 – Congruent Triangles 9.1 – Introduction Name ________________________________ Per _______ Date _______________________ 3. What is common? What is different? Is there a rigid motion that shows they are congruent? 4. Based upon your results, what are some conjectures about when triangles are congruent? HIDOE Geometry SY 2016-2017 20 L9 – Congruent Triangles 9.2 – Determining Congruence Name __________________________________ Per _______ Date _______________________ Grandma’s Garden Boxes Grandma has been watching the garden channel again. She fell in love with some triangular shaped raised garden boxes. She asked Uncle Bobby to build them, but Uncle Bobby did not want to measure all three sides and all three angles of all the triangles. While he was complaining to you, you mentioned that you heard a rumor that in order to be sure that two triangles are congruent, you only need to measure three pieces of information. You just couldn’t remember what three pieces. Let’s investigate in the next activity. When you are finished with the activity, write a note to Uncle Bobby explaining what three measurements he would need to make sure the triangles are congruent. Note to Uncle Bobby: HIDOE Geometry SY 2016-2017 21 L9 – Congruent Triangles 9.2 – Determining Congruence Name __________________________________ Per _______ Date _______________________ WHAT DOES IT TAKE TO BE THE SAME? This exercise investigates critical theorems for proving when two triangles must be congruent. You will be able to use these theorems throughout the remainder of the course. Scenario 1: Side-Side-Side (SSS) In this scenario you will explore if having three sides of one triangle congruent to three sides of another triangle guarantees that the two triangles are congruent. 1. Draw a scalene triangle on a sheet of tissue paper. 2. Using three other pieces of tissue paper, trace each of the sides of the triangle onto a separate piece of paper. Mark the ends of each segment to make them easier to see. 3. Slide the three pieces together to make a triangle and copy the new triangle onto another piece of tissue paper. 4. Is your new triangle congruent to the original? Explain why or why not. 5. Can you rearrange the pieces to create a new triangle that is not congruent to the original? Explain why the two triangles must be congruent, or why not. 6. State your Claim: If three sides of one triangle are congruent to three sides of another triangle, then ______________________________________________________________________.(#THM) HIDOE Geometry SY 2016-2017 22 L9 – Congruent Triangles 9.2 – Determining Congruence Name __________________________________ Per _______ Date _______________________ Scenario 2: Angle-Angle-Angle (AAA) In this scenario you will explore if having three angles of one triangle congruent to three angles of another triangle guarantees that the two triangles are congruent. 1. Draw a scalene triangle on a sheet of tissue paper. 2. Using three other pieces of tissue paper, trace each of the angles of the triangle onto a separate piece of paper. Extend the rays of the angles. 3. Slide the three pieces together to make a new triangle and copy the new triangle onto another piece of tissue paper. Recall that a ray has no end, hence you will only be using a portion of each ray as a side. 4. Is your new triangle congruent to the original? Explain why or why not. 5. Can you rearrange the pieces to create a new triangle that is not congruent to the original? Explain why the two triangles must be congruent, or why not. 6. State your Claim: If three angles of one triangle are congruent to three angles of another triangle, then __________________________________________________________________ HIDOE Geometry SY 2016-2017 23 L9 – Congruent Triangles 9.2 – Determining Congruence Name __________________________________ Per _______ Date _______________________ Scenario 3: Side-Side-Angle (SSA) In this scenario you will explore if having two concurrent sides and the angle adjacent to the second side of one triangle congruent to two concurrent sides and the angle adjacent to the second side of another triangle guarantees that the two triangles are congruent. 1. Draw a scalene triangle on a sheet of tissue paper. 2. Using three other pieces of tissue paper, trace two concurrent sides and the angle adjacent to the second side (i.e. opposite the first side) of one triangle onto a separate piece of paper. Mark the ends of each segment to make them easier to see, making sure you keep track of which side was the first side, and extend the rays of the angles. 3. Slide the three pieces together to make a new triangle, making sure the angle is still opposite the first side, and copy the new triangle onto another piece of tissue paper. Recall that a ray has no end, hence you will only be using a portion of each ray as a side. 4. Is your new triangle congruent to the original? Explain why or why not. 5. Can you rearrange the pieces to create a new triangle that is not congruent to the original, where the angle is still opposite the first side? Explain why the two triangles must be congruent, or why not. 6. State your Claim: If two concurrent sides and the angle adjacent to the second side of one triangle are congruent to two concurrent sides and the angle adjacent to the second side of another triangle, then _____________________________________________________________________ HIDOE Geometry SY 2016-2017 24 L9 – Congruent Triangles 9.2 – Determining Congruence Name __________________________________ Per _______ Date _______________________ Scenario 4: Side-Angle-Side (SAS) In this scenario you will explore if having two sides and the angle between them of one triangle congruent to two sides and the angle between them of another triangle guarantees that the two triangles are congruent. 1. Draw a scalene triangle on a sheet of tissue paper. 2. Using three other pieces of tissue paper, trace two sides and the angle between them of the triangle onto a separate piece of paper. Mark the ends of each segment to make them easier to see and extend the rays of the angles. Recall that a ray has no end, hence you will only be using a portion of each ray as a side. 3. Slide the three pieces together to make a new triangle, making sure the angle is still between the two sides, and copy the new triangle onto another piece of tissue paper. Recall that a ray has no end, hence you will only be using a portion of each ray as a side. 4. Is your new triangle congruent to the original? Explain why or why not. 5. Can you rearrange the pieces to create a new triangle that is not congruent to the original, where the angle is still between the two sides? Explain why the two triangles must be congruent, or why not. 6. State your Claim: If two sides and the angle between them of one triangle are congruent to two sides and the angle between them of another triangle, then ___________________________________________________________________. (#THM) HIDOE Geometry SY 2016-2017 25 L9 – Congruent Triangles 9.2 – Determining Congruence Name __________________________________ Per _______ Date _______________________ Scenario 5: Side-Angle-Angle (SAA) In this scenario you will explore if having two angles and the side not between them of one triangle congruent to two angles and one of the sides not between them, of another triangle guarantees that the two triangles are congruent. 1. Draw a scalene triangle on a sheet of tissue paper. 2. Using three other pieces of tissue paper, trace two angles and one of the sides not between them of the triangle onto a separate piece of paper. Mark the ends of each segment to make them easier to see and extend the rays of the angles. 3. Slide the three pieces together to make a new triangle, making sure the side is still not between the two angles, and copy the new triangle onto another piece of tissue paper. Recall that a ray has no end, hence you will only be using a portion of each ray as a side. 4. Is your new triangle congruent to the original? Explain why or why not. 5. Can you rearrange the pieces to create a new triangle that is not congruent to the original, making sure the side is still not between the two angles? Explain why the two triangles must be congruent, or why not. 6. State your Claim: If two angles and the side not between them of one triangle are congruent to two angles and the side not between them of another triangle, then ___________________________________________________________________.(#THM) HIDOE Geometry SY 2016-2017 26 L9 – Congruent Triangles 9.2 – Determining Congruence Name __________________________________ Per _______ Date _______________________ Scenario 6: Angle-Side-Angle (ASA) In this scenario you will explore if having two angles and the side between them of one triangle congruent to two angles and the side between them of another triangle guarantees that the two triangles are congruent. 1. Draw a scalene triangle on a sheet of tissue paper. 2. Using three other pieces of tissue paper, trace two angles and the side between them of the triangle onto a separate piece of paper. Mark the ends of each segment to make them easier to see and extend the rays of the angles. 3. Slide the three pieces together to make a new triangle, making sure the side is still between the two angles, and copy the new triangle onto another piece of tissue paper. Recall that a ray has no end, hence you will only be using a portion of each ray as a side. 4. Is your new triangle congruent to the original? Explain why or why not. 5. Can you rearrange the pieces to create a new triangle that is not congruent to the original, making sure the side is still between the two angles? Explain why the two triangles must be congruent, or why not. 6. State your Claim: If two angles and the side between them of one triangle are congruent to two angles and the side between them of another triangle, then ___________________________________________________________________.(#THM) HIDOE Geometry SY 2016-2017 27 L9 – Congruent Triangles 9.2 – Determining Congruence Name __________________________________ Per _______ Date _______________________ Summary Complete the following. Use this sheet as a summary for your class and homework. 1. List the four Congruence Theorems here. Write the acronym and then describe what that acronym means. Be specific and clear when describing an angle or side. 2. By definition, congruent triangles have ______________________________ and _____________________________________. 3. Thus, we can say “Corresponding parts of ____________________ triangles are _______________________.” (#THM) We use this statement very often in geometry. When we use it, we use an acronym, CPCTC. Congruence Statement If ∆𝐴𝐵𝐶 is congruent to ∆𝐷𝐸𝐹, then we write ∆𝐴𝐵𝐶 ≅ ∆𝐷𝐸𝐹. So, if ∆𝐴𝐵𝐶 ≅ ∆𝐷𝐸𝐹 then complete the following: ∠𝐸 ≅ ______ 𝐴𝐵 ≅______ ∠𝐶 ≅______ 𝐸𝐹 ≅______ ∠𝐷 ≅______ 𝐴𝐶 ≅______ Now go back to grandma’s garden boxes and write your note to Uncle Bobby. HIDOE Geometry SY 2016-2017 28 L9 – Congruent Triangles 9.3 – Identifying Congruent Triangles Name __________________________________ Per _______ Date ________________________ Are We Identical Twins? Which of the following pairs of triangles are congruent? Explain which criteria for triangle congruence you used to determine your answer. 1. Are the triangles congruent? Explain why or why not. 2. Are the triangles congruent? Explain why or why not. 3. Are the triangles congruent? Explain why or why not. 4. Are the triangles congruent? Explain why or why not. HIDOE Geometry SY 2016-2017 29 L9 – Congruent Triangles 9.3 – Identifying Congruent Triangles Name __________________________________ Per _______ Date ________________________ 5. Are the triangles congruent? Explain why or why not. 6. Are the triangles congruent? Explain why or why not. 7. Are the triangles congruent? Explain why or why not. HIDOE Geometry SY 2016-2017 30 L9 – Congruent Triangles 9.4 – Homework 1 Name __________________________________ Per _______ Date _______________________ Congruent Triangles Homework There are four pairs of congruent triangles. State how you know they are congruent using the measurements of the sides and/or angles. You have four methods to use to prove they are congruent: SSS, SAS, ASA, and AAS. Once you use one method, you may not use it again. Thus, you must use a different method for each pair. Label each triangle and write a congruence statement for each. 1. Congruence Statement ______________________ Reason _______________ 2. Congruence Statement ______________________ Reason _______________ HIDOE Geometry SY 2016-2017 31 L9 – Congruent Triangles 9.4 – Homework 1 Name __________________________________ Per _______ Date _______________________ 3. Congruence Statement ______________________ Reason _______________ 4. Congruence Statement ______________________ Reason _______________ HIDOE Geometry SY 2016-2017 32 L9 – Congruent Triangles 9.4 – Homework 1 Name __________________________________ Per _______ Date _______________________ CPCTC means _________________________________________________________ ______________________________________________________________________ Using the congruent statement, solve for x. Then, give the length of the sides for each triangle. ∆𝐵𝐶𝐷 ≅ ∆𝐹𝐻𝐺 G B 𝑥 + 5 𝑥 + 3 11.5 F 2𝑥 − 3 C D H 𝐵𝐶 =_________ 𝐹𝐻 =_________ 𝐵𝐷 =_________ 𝐹𝐺 =_________ 𝐷𝐶 =_________ 𝐺𝐻 =_________ Using the above triangles, we are given that 𝑚∠𝐷 = (4𝑦 + 12)° and𝑚∠𝐶 = (5𝑦 − 8)° and 𝑚∠𝐹 = (6𝑦 − 34)°. Solve for y and use y to find all the angle measures. 𝑦 = ___________ 𝑚∠𝐷 = ___________° 𝑚∠𝐹 = ___________° 𝑚∠𝐶 = ___________° 𝑚∠𝐻 = ___________° 𝑚∠𝐵 = ___________° 𝑚∠𝐺 = ___________° HIDOE Geometry SY 2016-2017 33 HIDOE Geometry SY 2016-2017 34 L9 – Congruent Triangles 9.5 Proving Congruent Triangles Name __________________________________ Per _______ Date _______________________ Now we will use SSS, SAS, ASA, AAS and CPCTC to prove statements involving congruent triangles. 1. Given: Aisthemidpointof CE Aisthemidpointof BD Prove: ΔBCA ≅ ΔDEA Whattransformationcouldtake ΔBCA onto ΔDEA ?__________________________ Statement Reason HIDOE Geometry SY 2016-2017 35 L9 – Congruent Triangles 9.5 Proving Congruent Triangles 2. Given: Name __________________________________ Per _______ Date _______________________ GH ! JI ∠G ≅ ∠I GJ ≅ IH Prove: Whattransformationcouldtake ΔJGH onto ΔHIJ ?__________________________ Statement Reason HIDOE Geometry SY 2016-2017 36 L9 – Congruent Triangles 9.6 – Homework 2 Name __________________________________ Per _______ Date _______________________ Prove the following statements. OR and SP bisect each other 1. Given: ΔONP ≅ ΔRNS Prove: Statement Reason 2. Given: ∠JKM ≅ ∠LKM ∠JMK ≅ ∠LMK Prove: JM ≅ LM Statement Reason HIDOE Geometry SY 2016-2017 37 L9 – Congruent Triangles 9.6 – Homework 2 3. Given: Name __________________________________ Per _______ Date _______________________ R is the midpoint of QS QT ≅ ST Prove: ΔQRT ≅ ΔSRT Statement Reason 4. Given: ∠U and ∠X are right angles. ∠W ≅ ∠Y UW ≅ YX ∠V ≅ ∠Z Prove: Statement Reason HIDOE Geometry SY 2016-2017 38 L10 – Perpendicular Lines and Triangles 10.1 – Construction Warmup Name _____________________________ Per _____ Date _____________________ 1. Use a straightedge and compass to construct the perpendicular bisector for the line below. A B 2. If P is a point on the perpendicular bisector that does not lie on the line segment AB, what can you say about the lengths AP and BP? HIDOE Geometry SY 2016-2017 39 L10 – Perpendicular Lines and Triangles 10.2 – Grandma’s Roof Name _____________________________ Per _____ Date _____________________ Grandma’s Roof It’s time to design the roof to Grandma’s House. Many roofs are shaped like isosceles triangles. 1. List below all the things you know about isosceles triangles. 2. Can any of these help us build an isosceles shaped roof? 3. Sketch several examples of an isosceles triangle. What are some of the ways you can test to see if it’s really isosceles? 4. Think about the perpendicular bisector, as depicted below. This can help us with building an isosceles triangle. Draw an isosceles triangle on the diagram below. How do you KNOW what you’ve drawn is isosceles? HIDOE Geometry SY 2016-2017 40 L10 – Perpendicular Lines and Triangles 10.2 – Grandma’s Roof Name _____________________________ Per _____ Date _____________________ 5. This construction can help us in building our roof. Imagine that this is the front view of Grandma’s house. What are the four steps you would follow to sketch the roof in such a manner that you could be assured your roof would be isosceles? 6. Choose how high you want Grandma’s roof, and make a sketch of the house roof below. 7. Grandma sees your plans and decides she wants a roof that is half as tall in the middle. Draw this shorter roof on the same sketch above. In both examples, which sides of the roof triangle appear to be congruent? HIDOE Geometry SY 2016-2017 41 L10 – Perpendicular Lines and Triangles 10.2 – Grandma’s Roof Name _____________________________ Per _____ Date _____________________ 8. Let’s take a break from our building project to do a quick proof. Given: Point P is located on the perpendicular bisector of line segment AB. Prove: 𝑃𝐴 ≅ 𝑃𝐵 C P A Statement Reason 1. 1. Given 2. ????? 𝐴𝑀 ≅ ______ 2. ????? ≅ ______ 3. 𝑃𝑀 3. 4. 4. 5. _________ ≅ ________ 5. ???? ≅ 𝑃𝐵 ???? 6. 𝑃𝐴 6. B M ______ You just proved the Perpendicular Bisector Theorem: Any point on the perpendicular bisector of a line segment will be __________________ from the two endpoints of that line segment. (#THM). You should take particular note of the Perpendicular Bisector Theorem, and its Converse, which follows. They are very powerful theorems and appear throughout the study of geometry. HIDOE Geometry SY 2016-2017 42 L10 – Perpendicular Lines and Triangles 10.2 – Grandma’s Roof Name _____________________________ Per _____ Date _____________________ 9. Let’s do another isosceles triangle proof. • First, use patty paper to reproduce the triangle STU. • Fold the patty paper in such a way that the fold contains the midpoint of 𝑆𝑈and the point T. • Which angles appear to be equal? Let’s prove it! T Given: In triangle STU, 𝑆𝑇 ≅ 𝑇𝑈 Prove: ÐS @ ÐU Hint: First draw the angle bisector of ∠T Statement S U Reason The Isosceles Triangle Theorem: If two sides of a triangle are ______________________ , then the angles opposite those sides are also ______________________ . (#THM) 10. Make a conjecture for the converse of this theorem: If two angles of a triangle are ____________________, then the _________ opposite ____________ are also ____________________. HIDOE Geometry SY 2016-2017 43 L10 – Perpendicular Lines and Triangles 10.2 – Grandma’s Roof Name _____________________________ Per _____ Date _____________________ Note: The Isosceles Triangle Theorem is equivalent to the Converse of the Perpendicular Bisector Theorem: If 𝑃𝐴 ≅ 𝑃𝐵 then P must lie on the perpendicular bisector of line segment AB. (#THM) Thus, when you drop down a perpendicular line from the peak to the base, it must bisect the base (as long as you already know the two sides are equal, which is given). 11. Use what you just learned about the Isosceles Triangle Theorem to construct an isosceles triangle roof for grandma’s house, using only a compass and straightedge. HIDOE Geometry SY 2016-2017 44 L10 – Perpendicular Lines and Triangles 10.2 – Grandma’s Roof Name _____________________________ Per _____ Date _____________________ Distance from a point to line 12. Given: 𝐴𝐸 bisects ÐHAT and point P lies on 𝐴𝐸 H Prove: 𝐾𝑃 ≅ 𝑃𝐿 E K P A L *Hint: use the triangles Statement T Reason You just proved Theorem 10.1 (#THM): Given an angle bisector, all points on that bisector are ______________________________ from the sides of the angle. 13. Work with a partner to come up with a converse for Theorem 10.1. Write the converse statement below and then add it to your Theorem Booklet (#THM). HIDOE Geometry SY 2016-2017 45 L10 – Perpendicular Lines and Triangles 10.2 – Grandma’s Roof 14. Name _____________________________ Per _____ Date _____________________ X Given: Triangle XYZ is equilateral. Prove: ÐX @ ÐY @ ÐZ Y Statement Z Reason _______________ 1. 1. Given ???? ≅ ______ ≅ ______ 2. 𝑋𝑌 2. 3. 3. Isosceles Triangle Theorem 4. 4. Isosceles Triangle Theorem 5. 5. Theorem 10.2: An equilateral triangle is also _______________________________, and each angle has a measure of ______. (#THM) HIDOE Geometry SY 2016-2017 46 L10 – Perpendicular Lines and Triangles 10.3 – Homework Name _____________________________ Per _____ Date _____________________ Part I: Find the measure of the indicated side or angle. 1. 𝑊𝑌 2. 𝐽𝐷 W 3. 𝐴𝑇 F K 12 in 7 mi 7 cm J 9 mi D A Y U 4. mÐV T 5. T mÐX Y 68° R S 41° V X Part II:For exercises 6 – 10, refer to the diagram on the right. Set-up and solve an equation using the information provided. 6. LM = 5, LO = x 7. LM = 2x + 4, LO = 18 8. 9. LM = 3x - 6, LO = 2x + 21 𝑚∠𝑀 = 20 + 𝑥, 𝑚∠0 = 90 − 𝑥 L M HIDOE Geometry SY 2016-2017 O 47 L10 – Perpendicular Lines and Triangles 10.3 – Homework Name _____________________________ Per _____ Date _____________________ Part III:For exercises 11 – 14, refer to the diagram on the right. Set-up and solve an equation using the information provided. In the diagram, 𝐸𝐾 bisects ÐYEH 10. AP = 𝑥 − 5 and PB = −2𝑥 + 25 Y K A P 11. AP = 4𝑥 R − 12 and PB = 2𝑥 R + 6 E 12. 𝑚∠𝑌𝐸𝐻 = 82∘ 𝑎𝑛𝑑𝑚∠𝐵𝐸𝑃 = 4𝑥 + 9 13. B H ∠𝑌𝐸𝐻 = 82∘ 𝑎𝑛𝑑𝑚∠𝐵𝐸𝑃 = 7𝑥 C 14. Prove the Converse of the Isosceles Triangle Theorem. Given: ∠𝐴 ≅ ∠𝐵 in triangle ABC Prove: 𝐴𝐶 ≅ 𝐵𝐶 Statement Reason A HIDOE Geometry SY 2016-2017 B 48 L10 – Perpendicular Lines and Triangles 10.3 – Homework 15. Name _____________________________ Per _____ Date _____________________ Given: 𝐵𝐶 ≅ 𝐶𝐷 ≅ 𝐷𝐸, ∠𝐹𝐷𝐸 ≅ ∠𝐹 C Prove: ΔBCD ≅ ΔFED B D F E Statement HIDOE Geometry SY 2016-2017 Reason 49 HIDOE Geometry SY 2016-2017 50 L10 – Perpendicular Lines and Triangles 10.4 – Attic Access Revisited Name _____________________________ Per _____ Date _____________________ In the previous lesson we proved Theorem 10.1: Given an angle bisector, all points on that bisector are equidistant from the sides of the angle. This theorem can be helpful when planning to design Grandma’s attic. To ensure that opening to the attic opening is the closest distance to both sides of the roof, Theorem 10.1 tells us that the opening should be located on the angle bisector of the peak angle (as depicted in the sketch below). Angle Bisector Theorem (#THM): If a ray bisects an angle of a triangle, then it divides the opposite side into segments proportional to the other two sides of the triangle. For example, in the diagram below, since DB is half of CA, the angle bisector theorem tell us that Y is half of X. C 20’ A 10’ D X Y B 1. If the length of AB is 24’, what must be the values for X and Y? 2. If the length of AB is 25’, what must be the values for X and Y? HIDOE Geometry SY 2016-2017 51 HIDOE Geometry SY 2016-2017 52 L10 – Perpendicular Lines and Triangles 10.5 – Finding the Center of Revolution Name _____________________________ Per _____ Date _____________________ 1. Δ𝐴𝐵𝐶 below was rotated 180° about point D. Find point D. Hint: when a single point P is rotated about point D, the distance from its image P’ and D remains the same as from P to D. a. Verify that AD = A’D, BD = B’D and CD = C’D. b. Verify that the distance from the midpoint of BC to D is the same as the distance from the image of the midpoint of BC to D. HIDOE Geometry SY 2016-2017 53 L10 – Perpendicular Lines and Triangles 10.5 – Finding the Center of Revolution Name _____________________________ Per _____ Date _____________________ Recall the Converse of the Perpendicular Bisector Theorem: If point P is equidistant from points A and B, then P must lie on the perpendicular bisector of 𝐴𝐵. 2. When a figure is rotated 180° about a point, it is relatively easy to find the central point of rotation. When the figure is rotated X°, where X is NOT 180°, the problem becomes more difficult. We can use what we’ve learned in this lesson to locate the center. Let’s begin by rotating a point P, CW X° about a given point D, as illustrated in the diagram below. (D has purposefully been hidden, and the value for X is irrelevant to this discussion.) Since P is rotated about D, its image P’ must lie on the circle centered at D with radius PD. How might you be able to find D? Assume the dotted line circle is hidden from your view. a. Draw the line segment 𝑃𝑃′. b. The values PD and P’D must be _________________. c. Using your answer to part b, along with what you’ve learned in this lesson, it must be the case that D lies somewhere on the ___________________________ of𝑃𝑃′. d. Draw a line that must contain the point D. Note: since in a rotation problem you are not given the dotted-line circle, it is not possible to locate D with such limited information; you can only limit its location to being some point on a line. However, if your figure being rotated contains more than a single point, such as with a triangle for example, then you can use this technique on multiple points (e.g. the vertices) to find D. We do that in the next problem. HIDOE Geometry SY 2016-2017 54 L10 – Perpendicular Lines and Triangles 10.5 – Finding the Center of Revolution Name _____________________________ Per _____ Date _____________________ 3. Δ𝐸𝐹𝐺 below was rotated clockwise X° about point D. Find point D. Hint: Follow the technique used in the previous problem for the three vertices, along with the Converse of the Perpendicular Bisector Theorem. Reflections: a. Explain how to find the center of rotation when given a triangle and its rotated image. b. Do you think this technique would work with other figures? Why? c. How many pre-image/image pairs of points do you need to locate the center of rotation? HIDOE Geometry SY 2016-2017 55 HIDOE Geometry SY 2016-2017 56 L11 – Parallelograms and Quadrilaterals 11.1 – Revisiting Congruence Name _____________________________ Per _____ Date _____________________ Congruent Triangles Review: Decide whether or not each pair of triangles is congruent. If they are congruent, name the rule/theorem that proves that they are. Figures Congruent? If congruent, state the rule/theorem that justifies congruence A. Yes No B. Yes No Yes No C. 50° 100° 30° 50° 100° 30° HIDOE Geometry SY 2016-2017 57 L11 – Parallelograms and Quadrilaterals 11.1 – Revisiting Congruence Figures Name _____________________________ Per _____ Date _____________________ Congruent? If congruent, state the rule/theorem that justifies congruence D. Yes No E. Yes No Yes No F. 10m 8m 4m 10m 8m 4m HIDOE Geometry SY 2016-2017 58 L11 – Parallelograms and Quadrilaterals 11.2 – Properties of Parallelograms Name _____________________________ Per _____ Date _____________________ Grandma wants to install a window in the space shown in the diagram. Thinking about all the shapes she knows, she thinks a parallelogram may be a good fit for that space in the wall. To the right is a simple sketch of the wall the window is going in. Sketch a picture of what the rest of the window will look like in the diagram below. 2. What features do you think a parallelogram has? LEFTOFFRAME 1. (#VOC) Parallelogram: A four-sided figure where both pairs of opposite sides are parallel. HIDOE Geometry SY 2016-2017 59 L11 – Parallelograms and Quadrilaterals 11.2 – Properties of Parallelograms Name _____________________________ Per _____ Date _____________________ Investigation: 3. In order to determine what the window will look like, we need to construct the rest of the parallelogram. Do this by drawing the two remaining sides so they are parallel to their opposite sides. 4. Now measure all the side lengths of the parallelogram using your ruler or compass. Make a conjecture about the lengths of the opposite sides of a parallelogram: Myconjectureaboutthelengthsoftheoppositesidesofaparallelogram: HIDOE Geometry SY 2016-2017 60 L11 – Parallelograms and Quadrilaterals 11.2 – Properties of Parallelograms Name _____________________________ Per _____ Date _____________________ Grandma is not convinced. You only measured one example of a parallelogram that you sketched on a piece of paper. “You think all parallelograms have congruent opposite sides? Prove it!” If a quadrilateral is a parallelogram, then the opposite sides are congruent. (#THM) 5. Prove this theorem. • To do this proof, we want to draw a diagonal inside our parallelogram; this diagonal creates two triangles. We can use these triangles to help us prove many properties of parallelograms. C B D A Given: Quadrilateral ABCD is a parallelogram Hint: Use congruent triangles. Prove: 𝐶𝐵 ≅ 𝐷𝐴 and 𝐶𝐷 ≅ 𝐵𝐴 Statement HIDOE Geometry SY 2016-2017 Reason 61 L11 – Parallelograms and Quadrilaterals 11.2 – Properties of Parallelograms 6. Name _____________________________ Per _____ Date _____________________ Prove the converse of the theorem we just proved. If two opposite sides of a quadrilateral are parallel and congruent, then the quadrilateral is a parallelogram. (#THM) B C A D Given: 𝐶𝐵 ∥ 𝐷𝐴 and 𝐶𝐵 ≅ 𝐷𝐴 Prove: ABCD is a parallelogram. Statement HIDOE Geometry SY 2016-2017 Reason 62 L11 – Parallelograms and Quadrilaterals 11.2 – Properties of Parallelograms 7. Name _____________________________ Per _____ Date _____________________ If the only information we are given about a parallelogram is that both pairs of opposite sides of are congruent, can we prove that the quadrilateral must be a parallelogram? Ifthetwopairsofoppositesidesofaquadrilateralarecongruent, thenthequadrilateralisaparallelogram.(#THM) D Given:𝐷𝐴 ≅ 𝐶𝐵and𝐶𝐷 ≅ 𝐵𝐴. Prove:ABCDisaparallelogram. A C B Statement HIDOE Geometry SY 2016-2017 Reason 63 HIDOE Geometry SY 2016-2017 64 L11 – Parallelograms and Quadrilaterals 11.3 – Homework 1. D Name _____________________________ Per _____ Date _____________________ Inthefigurebelow,ABCDisaparallelogram. • Usewhatyouknowaboutpropertiesofparallelogramstoset-upandsolvean equationtodeterminethevalueofx. • Then,useyoursolutiontodeterminetheperimeteroftheparallelogram. 𝟑𝒙 + 𝟔 A C 2. 𝒙 B 𝟓𝒙 − 𝟓 Circlethequadrilateralsbelowthatyouknowforsureareparallelograms.Diagramsarenot drawntoscale. A. B. C. D. HIDOE Geometry SY 2016-2017 65 HIDOE Geometry SY 2016-2017 66 L11 – Parallelograms and Quadrilaterals 11.4 – Parallelogram Angle Proofs Name _____________________________ Per _____ Date _____________________ Tocuttheglassforthewindowintoaparallelogram,theglasscompanyneedstoknowthe measureofeachangleoftheparallelogram.Wehavealreadyprovedthattheoppositesidesmust bethesamelength.Butisitalsotruethatoppositeanglesmustbecongruent? Investigation: 1. Constructthreeuniqueparallelogram-shapedwindowsusingthesegmentprovidedforone sideoftheparallelogram.Note:constructeachparallelogramsothatadjacentsidesarenotthe samelength. A.ConstructparallelogramPQRSusing𝑃𝑄foronesideoftheparallelogram.Appropriatelylabel allfourverticesofyourparallelogram. P Q B.ConstructparallelogramEFGHusing𝐸𝐹foronesideoftheparallelogram.Appropriatelylabel allfourverticesofyourparallelogram. E HIDOE Geometry SY 2016-2017 F 67 L11 – Parallelograms and Quadrilaterals 11.4 – Parallelogram Angle Proofs Name _____________________________ Per _____ Date _____________________ C.ConstructparallelogramJKLMusing𝐽𝐾foronesideoftheparallelogram.Appropriatelylabel allfourverticesofyourparallelogram. J K 2. Forallthreeparallelogramsthatyoujustconstructed,useaprotractortomeasureeachangle (tothenearestdegree).Writethemeasureineachangle. 3. Analyzetheanglemeasureswithineachparallelogram.Maketwoconjecturesaboutthe measuresoftheangleswithinaparallelogram. HIDOE Geometry SY 2016-2017 68 L11 – Parallelograms and Quadrilaterals 11.4 – Parallelogram Angle Proofs Name _____________________________ Per _____ Date _____________________ 4. Aretheconsecutiveanglesofparallelogramsalwayssupplementary?Let’strytoproveit. Consecutiveanglesinaparallelogramaresupplementary.(#THM) Given:ABCDisaparallelogram. Prove:∠𝐶𝐷𝐴and∠𝐵𝐴𝐷aresupplementary. B C A D ***Inthediagramabove,eachsideoftheparallelogramhavebeenextended(withdashedlines) sothatitisalittleeasiertoseetheparallellines.Whathavewelearnedpreviouslyaboutthe relationshipsbetweenanglesformedwhenparallellinesarecutbyatransversal? Statement Reason HIDOE Geometry SY 2016-2017 69 L11 – Parallelograms and Quadrilaterals 11.4 – Parallelogram Angle Proofs 5. Name _____________________________ Per _____ Date _____________________ Aretheoppositeanglesofparallelogramsalwayscongruent?Let’strytoproveit. Oppositeanglesofaparallelogramarecongruent.(#THM) Given:ABCDisaparallelogram. Prove:∠𝐶𝐷𝐴 ≅ ∠𝐶𝐵𝐴and∠𝐵𝐴𝐷 ≅ ∠𝐵𝐶𝐷 B C A D ***Inthediagramabove,adiagonalhasbeendrawninsideoftheparallelogram.Whatdoesthis diagonalcreateinsideoftheparallelogram?Howmightithelpusprove∠𝐶𝐷𝐴 ≅ ∠𝐶𝐵𝐴and ∠𝐵𝐴𝐷 ≅ ∠𝐵𝐶𝐷? Statement HIDOE Geometry SY 2016-2017 Reason 70 L11 – Parallelograms and Quadrilaterals 11.5 – Homework Name _____________________________ Per _____ Date _____________________ Forexercises1and2,thequadrilateralsshownareparallelograms.Eachvariablerepresentsthe measureoftheangle.Determinethevalueofeachvariable. 1. x 120° z y 2. 34° b c a 3.KPLRisaparallelogram.𝑚∠𝑃 = 7𝑥 − 75and𝑚∠𝑅 = 3𝑥 + 45.Set-upandsolveanequation, thenuseyoursolutiontodeterminethevalueofallfouranglesofparallelogramVWXY. K P R L HIDOE Geometry SY 2016-2017 71 HIDOE Geometry SY 2016-2017 72 L11 – Parallelograms and Quadrilaterals 11.6 – Diagonals of Parallelograms Name _____________________________ Per _____ Date _____________________ Often,interestingdesignscanbecreatedbydrawinginthediagonalsofafigure. Diagonalsofaparallelogramcanbedrawnbyconnectingbothpairsofoppositevertices. (#VOC)Diagonal:Alineconnectingnon-consecutiveverticesofapolygon. 1. Intheparallelogrambelow,usearuler(orastraight-edgetool)todrawthetwodiagonals. 2. Whentwodiagonalsintersect,theycuttheothertoformfoursmallerlinesegments? Measurethelengthsofthefourlinesegmentscreatedbythediagonalsinyourfigureabove. Writeeachmeasurenexttoeachsegment. 3. Analyzethelengthsofthefoursegmentsyoujustmeasured.Makeaconjectureaboutthe lengthsofthesegmentscreatedwhenyoudrawinbothdiagonalsofaparallelogram. 4. Repeatsteps1and2abovewiththebelowparallelogram.Doesyourconjecturestillhold? HIDOE Geometry SY 2016-2017 73 L11 – Parallelograms and Quadrilaterals 11.6 – Diagonals of Parallelograms Name _____________________________ Per _____ Date _____________________ 5. Dothediagonalsofaparallelogramsalwayscuteachotherintotwocongruentsegments? Let’strytoproveit. Thediagonalsofaparallelogrambisecteachother.(#THM) Given:ABCDisaParallelogram. 𝐶𝐴and𝐷𝐵arediagonalsofABCD. Prove:𝐷𝐸 ≅ 𝐸𝐵and𝐶𝐸 ≅ 𝐸𝐴 C B E A D Statement Reason HIDOE Geometry SY 2016-2017 74 L11 – Parallelograms and Quadrilaterals 11.6 – Diagonals of Parallelograms Name _____________________________ Per _____ Date _____________________ Grandmalikestheideaofhavingawindowintheshapeofaparallelogram.Butshedoesn’tlike thedesigncreatedbydrawinginthediagonalsoftheparallelogram Instead,shewantstohavethewindowintheshapeofaparallelogram,butwithonly2sections. Youthinkoftheideatoconnectthemidpointsofthetopandbottomsidesoftheparallelogram. Youdrawthediagrambelowandaskherwhatshethinks. 6. Let’sproveatheoremaboutthesegmentthatconnectsthemidpointsofoppositesidesofa parallelogram. Inaparallelogram,thelinesegmentcontainingthemidpointsofoppositesides isparalleltotheothertwosides.(#THM) Given:ABCDisaParallelogram. MandNarethemidpointsofthe oppositesides𝐴𝐷and𝐵𝐶,respectively. D Prove:𝑀𝑁isparallelto𝐷𝐶and𝐴𝐵 Statement M C A N B Reason HIDOE Geometry SY 2016-2017 75 L11 – Parallelograms and Quadrilaterals 11.6 – Diagonals of Parallelograms 7. Name _____________________________ Per _____ Date _____________________ Arectangleisaspecialparallelogrambecauseithasadditionalproperties.Several interestingthingshappenwhenwedrawinthediagonalsofarectangle. Let’sapplywhatwe’velearnedpreviouslyaboutdiagonalsofaparallelogramandcongruent trianglestocompletetheproofbelow. C X D Given:𝐶𝐴and𝐷𝐵arediagonalsofrectangleABCD Prove:DDAXisisosceles Statement HIDOE Geometry SY 2016-2017 B A Reason 76 L11 – Parallelograms and Quadrilaterals 11.7 – Congruent Quadrilaterals Name _____________________________ Per _____ Date _____________________ Recallthatininformalwaytoverifyiftwopolygonsarecongruentistoshowthatthefigures havethesamesizeandsameshape. 1.Foreachpairoffiguresbelow,answerthefollowingquestions. • Arethequadrilateralscongruent?Usepattyormeasuringtoolstoconfirmyouranswer. • Ifthequadrilateralsarecongruent,writecongruencestatementsthatindicateALLofthe correspondingsidesandanglesthatarecongruent(e.g.,𝐷𝐸 ≅ 𝐸𝐵). A. R J S K L T M U B. O V W P Q X N Y HIDOE Geometry SY 2016-2017 77 L11 – Parallelograms and Quadrilaterals 11.7 – Congruent Quadrilaterals Name _____________________________ Per _____ Date _____________________ Followingyourteacher’sinstructions,usethenextfewquestionstotakeguidednotesabout congruentquadrilaterals. 2.CongruentQuadrilaterals • Theyhaveexactlythesame_______________________________and_______________________________. • Youusearigidtransformationtoverifyiftheyarecongruent.Forexample,youcould _______________________________,_______________________________,or_______________________________ oneofthefiguressothatitfitsexactlyontheotherone. • • Corresponding_______________________________andcorresponding_______________________________ arecongruent. Whenwritingacongruencestatement,eachquadrilateralshouldbenamedsuchthatthe correspondingverticesappearinthe________________________________________________________. N 3. Thetwoquadrilateralsshownarecongruent. A A.Fillintheblankstoindicateallpairs ofcorrespondingvertices,sidesandangles. R Rcorrespondsto______ correspondsto____________ ÐRcorrespondsto___________ Ncorrespondsto______ correspondsto____________ ÐNcorrespondsto___________ Acorrespondsto______ correspondsto____________ ÐAcorrespondsto___________ Fcorrespondsto______ 𝐹𝑅correspondsto____________ ÐFcorrespondsto___________ Y G F L P B.Writethecongruencestatementforthetwoquadrilateralsshown:_______________________________ HIDOE Geometry SY 2016-2017 78 7.1 – Congruent Quadrilaterals Per_____ Date_______________________ Example 2: COAT ! KIND. Find: N Quadrilaterals – Congruence & Characteristics Name_______________________________ 8 cm L11 – Parallelograms and2Quadrilaterals Name _____________________________ 50° 7.1 – Congruent Quadrilaterals Per_____ Date_______________________ 11.7 – Congruent Quadrilaterals Per _____ Date _____________________ a) Use the congruence statement to O 50° list corresponding Example 2: vertices. COAT ! KIND. Find: A D N 8 cm 4.Forthefiguresshowntotheright,COAT@KIND. a) Use the congruence statement to O list corresponding vertices. A.Usethecongruencestatementtolist 130°50° correspondingvertices. C T b) m"A ____________correspondsto____________ 130° C ____________correspondsto____________ b) m"A 50° A D K 8 cm I T K c) m"D ____________correspondsto____________ 8 cm I ____________correspondsto____________ c) m"D C ! T d) AT B.mÐA= C.mÐD=____________ D. =____________ C T AT d)____________ Example 3: Find the value of the variables, x and y, if CHLD ! PNTS. T S C Example 3: Find the value of the variables, x and y, if CHLD ! PNTS. x T S 5. !Forthefiguresshowntotheright, • CHLD@PNTS • xrepresentsthemeasureofÐS • yrepresentsthelengthof𝐶𝐷 C 40° 4xyd y 40° 4 yd y D DN Determinethevaluesofxandy. 5 yd N H 3 yd H 3 yd • 4x+2representsthemeasureofÐR 17 mm H H (8z–2)° (8z–2)° • 5y–7representsthelengthof𝐴𝑇 • 8z–2representsthemeasureofÐH 21 mm P L 6. Forthefiguresshowntotheright, MATH@PRTY 5 yd L R Example 4: Find the value of the variables, x, y, and z, if MATH ! PRTY. Example 4: Find the value of the variables, x, y, and z, if MATH ! PRTY. • P T 8 mm (4x+2)° R P8 mm (4x+2)° P 17 mm T 38° 38° Y 21 mm Determinethevaluesofx,yandz. Geometry 5y–7 M M 90° A Geometry HIDOE Geometry SY 2016-2017 5y–7 90° A Q2 Quadrilaterals Handouts Q2 Quadrilaterals Handouts Page 4 Page 4 79 Y HIDOE Geometry SY 2016-2017 80 L11 – Parallelograms and Quadrilaterals 11.8 – Special Quadrilaterals and their Properties Name _____________________________ Per _____ Date _____________________ Followingyourteacher’sinstructions,usethenextfewquestionstotakeguidednotesabout specialquadrilaterals. 1. Reviewthedefinitionsofthefollowingspecialquadrilaterals. A. Quadrilateral:_____________________________________________________________________________________. B. Parallelogram:aquadrilateralwith____________________________________________________________. C. Rhombus:aPARALLELOGRAMwith_____________________________________________________.#VOC D. Rectangle:aPARALLELOGRAMwith_____________________________________________________.#VOC E. Square:aPARALLELOGRAMwith________________________________________________________.#VOC F. Trapezoid:aquadrilateralwith____________________________________________________________.VOC G. IsoscelesTrapezoid:aTRAPEZOID______________________________________________________.#VOC 2. 3. H. Kite:aquadrilateralwith__________________________________________________________________.#VOC Fromthefiguretotheright,whatcanyouconcludeabout𝐴𝐵and𝐶𝐷?Brieflyexplainhow youknowyourconclusionistrue. A B C D Fillintheblanktocreateatruestatement: Basedonthedefinitionsabove,therhombus,rectangleandsquareareallspecialtypesof _____________________________________________________. HIDOE Geometry SY 2016-2017 81 L11 – Parallelograms and Quadrilaterals 11.8 – Special Quadrilaterals and their Properties 4. Name _____________________________ Per _____ Date _____________________ Thediagrambelowshowsonewaytoorganizeourthinkingaboutspecialquadrilaterals. • Wecanclassifyquadrilateralsinto3categoriesbasedonthenumberofparallelsides thatthefigurehas: o nopairsofparallelsides o exactly1pairofparallelsides o 2pairsofparallelsides Completethediagrambywritingthenameofthespecialquadrilateralineachfigure. Quadrilateral HIDOE Geometry SY 2016-2017 82 L11 – Parallelograms and Quadrilaterals 11.8 – Special Quadrilaterals and their Properties 5. Name _____________________________ Per _____ Date _____________________ Workingwithapartner,usethedefinitionsandthediagramonthepreviouspagesto determineifthefollowingstatementsaretrueorfalse.Ifthestatementisfalse,eitherexplain whyordrawafigurethatshowsanexampleofwhythestatementisfalse. Statement True of False A. All trapezoids are quadrilaterals. True False B. All rectangles are squares. True False C. An isosceles trapezoid can be a kite. True False D. All squares are rhombuses. True False E. All parallelograms are rhombuses. True False If false, either explain why or draw afigurethatisacounterexample. HIDOE Geometry SY 2016-2017 83 L11 – Parallelograms and Quadrilaterals 11.8 – Special Quadrilaterals and their Properties 6. A. B. Name _____________________________ Per _____ Date _____________________ Findthevaluesofthevariablesandthelengthsofthesidesofeachquadrilateral. LMNO is a parallelogram. Determine the value of m and s. O 2m + 8 N s+1 L 5m - 2 3m - 1 M FGHI is a square. Determine the value of f and g. F 3f + 2 G 2g - 5 g+6 I H 5f - 8 HIDOE Geometry SY 2016-2017 84 L11 – Parallelograms and Quadrilaterals 11.8 – Special Quadrilaterals and their Properties 7. A. B. C. Name _____________________________ Per _____ Date _____________________ Usethequadrilateraltotherighttoanswerthefollowingquestions. 39° Based on the information provided for the figure, what is the most appropriate name for the quadrilateral? Provide a brief explanation why you selected that name. 3 Determine the sum of all 4 angles of the quadrilateral. Show or explain how you determined your answer. U Complete the following proof regarding the sum of the angles of any quadrilateral. Given:QuadrilateralQUADwithdiagonal𝑄𝐴 Prove:mÐQ+mÐU+mÐA+mÐD=360 1 Statement A Q D Reason HIDOE Geometry SY 2016-2017 85 HIDOE Geometry SY 2016-2017 86 L11 – Parallelograms and Quadrilaterals 11.9 – Theorems of Special Quadrilaterals Name _____________________________ Per _____ Date _____________________ PROPERTIESOFSPECIALQUADRILATERALS 1. Foreachquadrilateralbelow,dothefollowing: -drawinandmeasurethelengthsofthediagonals. -measureallanglesinthefigure. -choosethebestnameforthequadrilateral a) b) c) d) e) f) 2. Usingwhatyoulearnedabove, a. Whatcharacteristic(s)doallrectangleshave? Rectangleshave___________________________________________________ b. Whatcharacteristic(s)doallrhombihave? Rhombihave______________________________________________________ c. Whatcharacteristic(s)doallisoscelestrapezoidshave? Isoscelestrapezoidshave_____________________________________________ d. Whatcharacteristic(s)doallkiteshave? Kiteshave________________________________________________________ HIDOE Geometry SY 2016-2017 87 L11 – Parallelograms and Quadrilaterals 11.9 – Theorems of Special Quadrilaterals Name _____________________________ Per _____ Date _____________________ SPECIALQUADRILATERALTHEOREMS Theorem:Eachdiagonalofarhombus__________ twoanglesoftherhombus.#THM A D B C A B D Theorem:Thediagonalsofarhombusare__________. #THM C S T M Theorem:Thediagonalofarectangleare__________. #THM I E W V Y X Theorem:Baseanglesofanisoscelestrapezoidare_______________. #THM Theorem:Thediagonalsofanisoscelestrapezoidare___________. #THM P N Theorem:Thediagonalsofakiteare_______________. E HIDOE Geometry SY 2016-2017 H P U N H U K I T 88 L11 – Parallelograms and Quadrilaterals 11.9 – Theorems of Special Quadrilaterals Name _____________________________ Per _____ Date _____________________ 3.Foreachquadrilateral, • statethemostappropriatenameforthefigure • findthemeasureofeachnumberedangle(e.g.,1,2,3,4). 18° A. B. 54° 4 1 4 23 C. D. 121° 1 2 1 3 59° 4 E. F. 2 1 1 79° 65° HIDOE Geometry SY 2016-2017 2 3 1 2 2 89 L11 – Parallelograms and Quadrilaterals 11.9 – Theorems of Special Quadrilaterals Name _____________________________ Per _____ Date _____________________ 4. Theperimeterofakiteis80ft.Thelengthofoneofitssidesis5lessthan4timesthelength ofanother.Findthelengthofeachsideofthekite.Hint:Drawapicture. 5. Findthevalueofthevariables. A. B. (6x + 20)° 2x° 3x° y° 4x° (10x - 6)° C. 3x - 3 x-1 x+5 HIDOE Geometry SY 2016-2017 90 L11 – Parallelograms and Quadrilaterals 11.9 – Theorems of Special Quadrilaterals Name _____________________________ Per _____ Date _____________________ 6.ProvethefollowingTheorem:Diagonalsofarhombusbisectoppositeanglesofarhombus. S B Given:RhombusRMBSwithdiagonal𝑆𝑀 Prove:ÐRSM≅ÐBSMandÐRMS≅ÐBMS R M 7.ProvethefollowingTheorem:Thediagonalsofarectanglearecongruent. Given:RectangleRECT M A Prove:𝑀𝑇 ≅ 𝐻𝐴 HIDOE Geometry SY 2016-2017 H T 91 HIDOE Geometry SY 2016-2017 92 L12 – Dilations and Similarity 12.1 – Refresher on Ratios Name _____________________________ Per _____ Date _____________________ 1. Completethetablebelow.Thefirstrowiscompletedforyouasanexample. Equation 1 Equation 2 (equation 1 re-written so that the variables are on opposite sides of the equation) Interpretation of Equation 2 x =3 y x = 3y x is 3 times as big as y x to y is 3 x to y is ½ x =2 y x= 1 y 4 x is 5 times as big as y x to y is 0.3 2. Statetheratioofthelengthsofthefollowingpairsofsidesofthetriangle. `a ab = `b ab = 2 m. 1.5 m. `a 1 m. HIDOE Geometry SY 2016-2017 `b = `b `a = 93 L12 – Dilations and Similarity 12.1 – Refresher on Ratios Name _____________________________ Per _____ Date _____________________ 3. Ineachpicture,determineifthereisarigidmotiontransformationwhichtakesonefigureto theother.Ifnoneexists,explainwhy. B A C D E HIDOE Geometry SY 2016-2017 F 94 L12 – Dilations and Similarity 12.2 – Grandma’s Gazebo Name _____________________________ Per _____ Date _____________________ 1. Below is a bird’s eye view of Grandma’s Gazebo, as depicted on the architect’s blueprints. Because of her poor eyesight, Grandma is having difficultly seeing the details of the Gazebo drawing. Help her out by drawing a new version that is twice as big, by following the instructionsbelow. F E iii. iv. B G D i. ii. A C Fromthecenter,extendthedottedlinesegment GA tobetheray𝐺𝐴.Repeatfortheray𝐺𝐵. Measurethelengthofthelinesegments GA and GB .(Theyshouldbeequal,andinfactalso equaltoAB,since∆𝐴𝐵𝐺isequilateral.) Markthepoints A ' and B ' ontherays𝐺𝐴and𝐺𝐵,respectively,sothatthelinesegments GA ' and GB ' aretwiceaslongaslinesegments GA and GB .(Usearulerorcompass.) Nowmeasurethelengthofthelinesegment𝐴′𝐵′. a. Whatistherelationshipbetweenthelengthof𝐴′𝐵′andthelengthof𝐴𝐵? !##" !###" b. Howarethelines AB and A' B ' related?(Note:notthelinesegments,butthelines.) HIDOE Geometry SY 2016-2017 95 L12 – Dilations and Similarity 12.2 – Grandma’s Gazebo Name _____________________________ Per _____ Date _____________________ Imagine repeating Steps 3 and 4 at each vertex. What would be the shape of the resulting figure? c. Tryitout.RepeatSteps3and4ateachvertex.Whatdoyounotice? d. UsepattypaperoraprotractortocomparetheanglesABCandA’B’C’,andtheangles ABGandA’B’G.Whatdoyounotice? e. MeasurethedistancefromthecenterGtothemidpointof AB .Whatdoyouthink thedistanceisfromthecenterGtothemidpointof A ' B ' ?Tryitout. f. Repeatthiscomparisonforthelinesegmentsconnectingthemidpointsof AB and CD ,andthoseconnectingthemidpointsof A ' B ' and C ' D ' .Whatdoyounotice? g. Whatistheratioofthecorrespondingsidesbetweenthedouble-scaleddrawingand theoriginal? The ratio is: This means that when we extend the rays from a specific point of the gazebo by a multiple of _________, then the side lengths multiply by a factor of ______________. h. Whatistheratioofthecorrespondinganglesbetweenthedouble-scaleddrawing andtheoriginal? The ratio is: This means that when we extend the rays from a specific point of the gazebo by a multiple of _________, then the angles ____________________________. Whenweincreasethesizeofthegazebo,thelengthmeasurements_______________, buttheanglemeasurements____________________________. HIDOE Geometry SY 2016-2017 96 L12 – Dilations and Similarity 12.2 – Grandma’s Gazebo i. j. Name _____________________________ Per _____ Date _____________________ Whatdoyouthinktheratioofcorrespondingsideswouldbeifwehadcreatedatriplescalediagram? Whatdoyouthinktheratioofcorrespondingangleswouldbeifwehadcreatedatriplescalediagram? Summary: This dilation transformation seems to have preserved the _________________, but increased the ________________. HIDOE Geometry SY 2016-2017 97 L12 – Dilations and Similarity 12.2 – Grandma’s Gazebo Name _____________________________ Per _____ Date _____________________ 2. Grandma’seyesareprettyweak.Usetheprocesswejustcompletedearliertodrawacopyof thehexagongazebothatisthreetimeslargerthantheoriginalpicture. F E A B G D C A. What is the ratio of the diagonals of your new diagram to the original one? B. Do you think we would get a different result if we increased the size by an integer multiple (2, 3, 5, etc.)? For example, suppose we wanted to make the gazebo drawing 5.3 times as large; would we end up with the same result as above or would we get a different result? HIDOE Geometry SY 2016-2017 98 L12 – Dilations and Similarity 12.2 – Grandma’s Gazebo Name _____________________________ Per _____ Date _____________________ 3. Supposewetookahexagonwithsidelengthsof3inches(i.e.yourresultsfromtheprevious problem)andplaceditonthegroundsothatitscenterwasattheprecisecenterofwhere Grandmawilllocatehergazebo.Grandma’sGazebohassidelengthsof8feet.Calculatehow manytimeslargertheactualgazeboisthanthediagramplacedontheground,byfillinginthe followingblanks. Gazebo drawing side length: _________ inches Gazebo actual side length: _________ feet = ____________ inches How many times larger: _________________ a. Inordertobuildahexagonalgazebowith8ftsides,wewouldneedtoincreasethesizeof ourdiagrambyafactorof_______,whichiswhatwecallthesizeratiobetweenthetwo hexagons. b. Measuretheradiusofyour3-inchsidedGazebofromProblem2,itshouldalsobe3”. Therefore,theradiusoftheactualGazeboshouldbe_________________. c. Ifwewantedtoincreaseourcurrentdrawing(ofsidelength3inches)toalargerdrawing with1footsides,wewouldneedtoincreasethesizeofourdiagrambyafactorof______,the sizeratiobetweenthetwohexagons. d. This ratio is referred to as the scale factor (#VOC), which is a non-negative number that we use to increase or decrease the size of our image, while maintaining the same shape. 4. AssumeyouarethecontractorandyouneedtolayouttheGazebowith8ft.sides.Youknow wherethecenterislocated,butyouneedtolocateeachofthevertices.Youcanassumeyou haveaverylargecompass,sinceacompasscanbeemulatedwithastringattachedtoastakein theground(e.g.locatedatthecenteroftheGazebo),andthatyouhavea25ft.tapemeasure, whichisessentiallyalongruler.WhatstepswouldyoufollowtolayouttheGazebo?Note:you maychooseyourfirstvertexarbitrarily,aslongasitsdistancefromthecenteriscorrect. HIDOE Geometry SY 2016-2017 99 L12 – Dilations and Similarity 12.2 – Grandma’s Gazebo 5. Name _____________________________ Per _____ Date _____________________ Follow your teacher’s instructions to apply the concept of “scale factor” to compare, enlarge or compress various objects. Original object’s side lengths: ___________, ____________, ______________, ___________ Projected object’s side lengths: __________, ____________, ______________, ___________ Ratio between lengths: ___________, ____________, ______________, ___________ Therefore, scale factor is: ______________ HIDOE Geometry SY 2016-2017 100 L12 – Dilations and Similarity 12.2 – Grandma’s Gazebo 6. Name _____________________________ Per _____ Date _____________________ For each pair of figures below, thefigureonthelefthasbeendilatedtocreatethefigureon theright.Measurethelengthsofanysidesthatareneeded(inmillimeters)anduseyour measurementstostatethescalefactorbetweenthetwofigures. A. Scalefactor: B. Scalefactor: C. Scalefactor: D. Scalefactor: HIDOE Geometry SY 2016-2017 101 L12 – Dilations and Similarity 12.2 – Grandma’s Gazebo Name _____________________________ Per _____ Date _____________________ 7. Pairupthefollowingtrianglesthatappeartoberelatedbyadilation. • • Then,measurethelengthofeachsidetohelpyoudetermineifthefiguresrepresentan actualdilation. Ifso,statethescalefactorthatwasusedtodilatethefirstfiguretocreatethesecond figure. B A C D E Pair 1: F & _______________ Scale Factor: _________________ Pair 2: C & _______________ Scale Factor: _________________ Pair 3: D & _______________ Scale Factor: _________________ HIDOE Geometry SY 2016-2017 F 102 L12 – Dilations and Similarity 12.3 – Dilations Name _____________________________ Per _____ Date _____________________ The type of transformation that we used to enlarge Grandma’s Gazebo, where we expanded our figure from its center, is an example of a special type of non-rigid transformation that we refer to as dilation, which we will formally define below. Let’s try to dilate figures from points other than a center. 1. Belowis DABC .Dilatethistrianglebyascalefactorof2fromvertexAandlabelthenew triangle DAB ' C ' .HerepointAisplayingthesameroleaspointGintheGazeboexercise. Followthesamestepsusedthere(i.e.drawaraywithendpointAthroughpointB,etc.) B A C 2. Check that your work is accurate. Measure each side length of DABC and DAB ' C ' to determine if the ratio of their lengths confirms our scale factor of 2. Show your work below. Remember to label your measurements with the side lengths they represent. 3. Are the angles of the new triangle the same as the corresponding angles of the original triangle? 4. When dilating a triangle using one of its vertices as the center of dilation, how many individual image points completely determine the entire image? HIDOE Geometry SY 2016-2017 103 L12 – Dilations and Similarity 12.3 – Dilations 5. Name _____________________________ Per _____ Date _____________________ WorkwithapartnertodiscussandanswerquestionsA–Dbelow. A. Howdoestheimageofadiagramcomparetotheoriginaldiagramwhenitisdilatedusinga scalefactorof2? B. Howdoestheimageofadiagramcomparetotheoriginaldiagramwhenitisdilatedusinga scalefactorof1? C. Howdoestheimageofadiagramcomparetotheoriginaldiagramwhenitisdilatedusinga scalefactorof½? D. Howdoestheimageofadiagramcomparetotheoriginaldiagramwhenitisdilatedusinga scalefactorof1.5? 6. Nowthatyouhavepracticedtheskillofdilationfromavertex,practicethisnon-rigid transformationonthetrianglesbelowwithnon-integerscalefactors(usingpattypaperand astraightedge). A. DEFG dilatedto DEF ' G ' withscalefactorof1.5 E G F HIDOE Geometry SY 2016-2017 104 L12 – Dilations and Similarity 12.3 – Dilations Name _____________________________ Per _____ Date _____________________ B. DKLM dilatedto DK ' L ' M withascalefactorof0.5 K L M C. DQRS dilatedto DQ ' RS ' withscalefactor2.5 R S Q HIDOE Geometry SY 2016-2017 105 L12 – Dilations and Similarity 12.3 – Dilations 7. Name _____________________________ Per _____ Date _____________________ We now move to the most general type of dilation, where the point of dilation is outside the figure. Follow the directions below to dilate DABC from point D with a scale factor of 2. D B C A i. Drawrays𝐷𝐴and𝐷𝐵. ii. MeasurethelengthsDAandDB. iii. MarkthepointA’andB’ontherays𝐷𝐴and𝐷𝐵,respectively,sothatthelinesegments DA ' and DB ' aretwiceaslongaslinesegments DA and DB .(Inotherwords,pointsA’andB’ aretwiceasfarfromDasAandB,respectively.) Howarethelengths AB and A ' B ' related? !##" !###" !##" !####" !##" !####" Howarethelines AB and A' B ' related?Whatabout AC and A'C ' , BC and B 'C ' . iv. RepeatthisprocessforpointCtoformtriangleA’B’C’. v. Usepattypaperoraprotractortocomparecorrespondinganglesinthetwotriangles.What doyounoticeaboutthecorrespondinganglesinthetwotriangles? HIDOE Geometry SY 2016-2017 106 L12 – Dilations and Similarity 12.3 – Dilations Name _____________________________ Per _____ Date _____________________ You have now seen 3 types of dilation: 1) from the center of the figure (Grandma’s Gazebo) 2) from a vertex of a figure, and 3) from a point outside a figure. A dilation with center D and scale factor r (#VOC) is a transformation that takes each point P (P not equal to D) to a point P’ along the ray 𝐷𝑃 such that the ratio of the distances (Note: Unless the scale factor is 1, a dilation is not a rigid transformation). 8. cd e cd = 𝑟. Follow your teacher’s instructions and use the space below to take guided notes. A. A scale factor is a ___________________ number. B. A dilation from point D with scale factor r takes a line segment of length L to a line segment of length r L . In other words, if the image under this dilation of line segment AB is the line segment A ' B ' , then the _______________of A ' B ' is r-times the length of _____________. !##" !###" C. Furthermore, the lines AB and A' B ' are _______________. As a result, the image of a dilation of a polygon will result in a polygon that has the same ____________________________but the length of the _______________will be ____________________________by a factor of r. D. A dilation with center D and scale factor r takes a line not containing D to a _________________________________________. E. A dilation with center D and scale factor r takes a line containing D to _________________________________________. F. A dilation with center D and a scale factor r takes an angle formed by rays AB and AC to a _____________________________. In order to dilate a triangle, using one of the vertices as the center of dilation, you only need to locate the image for __________________________ in order to completely determine the dilated image. HIDOE Geometry SY 2016-2017 107 HIDOE Geometry SY 2016-2017 108 L12 – Dilations and Similarity 12.4 – Introduction to Similarity Name _____________________________ Per _____ Date _____________________ A fundamental question in Geometry is “Does Figure A have the same shape as Figure B?” What we have seen is that the image of a dilation has the same shape as its pre-image. Two such objects, the image and the pre-image, are said to be similar. Before formalizing the meaning of similarity, let’s intuitively investigate the connection between this important concept and congruence. 1. Thefollowingpairsofobjectsintuitivelyappeartobesimilarinthesensethattheyappearto havethesameshape.Usepattypaperoraprotractortocheckthecongruencyoftheir correspondingangles. HIDOE Geometry SY 2016-2017 109 L12 – Dilations and Similarity 12.4 – Introduction to Similarity Name _____________________________ Per _____ Date _____________________ 2. Onewaytodetermineifapairoffiguresissimilaristoattempttomatchuptheangles.However, sincethesizeofthefiguresdiffer,youcanonlymatchuponeangleatatime. Gobackandtraceontopattypaperthefigureontherightineachofthethreepreviouspairs. Laythepattypaperwiththefigureyoutracedapproximatelywhereitwaspreviouslylocated. Slideitaround,asifyouwereapplyingarigidmotiontransformationuntiloneofthevertices anditsanglematches.Note:youmayalsoneedtoflipyourpattypaperoverifareflectionis required.Nowthatanangleismatchedup,doesthereappeartobeadilationthatwould transformthesmallerfigureintothelargerfigure? Whatistheapproximatescalefactorforeachpair? 3. Let’sinvestigatetheconnectionbetweensameshapeandcongruencewithafinalexample. a. TranslateΔ𝐴𝐵𝐶belowuntilvertexAcoincideswithvertexD.Usepattypaperorcutout Δ𝐴𝐵𝐶. b. RotatethisimageofΔ𝐴𝐵𝐶anappropriateamountclockwiseuntil𝐴𝐶ishorizontal(asis linesegment𝐷𝐹). c. ReflectthesmallertriangleimageovertheverticallinepassingthroughpointD. E B A D F C It should now be clear that angles A and D are congruent, and further, if you were to dilate the smaller triangle by an appropriate scale factor it would coincide precisely with Δ𝐷𝐸𝐹, which shows the two triangles have congruent angles. In conclusion, a similarity transformation (#VOC) is a rigid motion transformation (e.g. the translation, rotation, and reflection used above) followed by a dilation. Similarity transformations demonstrate the connection between objects that have the same shape, but are not congruent (i.e. they can be made congruent via an appropriate dilation). Figure 1 and Figure 2 are said to be similar (#VOC) if Figure 2 is the image of Figure 1 under a similarity transformation (e.g. Δ𝐷𝐸𝐹 coincided with the image of the similarity transformation of Δ𝐴𝐵𝐶, so the two triangles are similar, which simply means they have congruent corresponding angles). The notation we use is Δ𝐴𝐵𝐶~Δ𝐷𝐸𝐹. HIDOE Geometry SY 2016-2017 110 L12 – Dilations and Similarity 12.4 – Introduction to Similarity Name _____________________________ Per _____ Date _____________________ 4. Twoboatsleaveadockatthesametime.BoatAtravels10milesperhourdirectlysouthand BoatBtravels30milesperhourdirectlyEast(Seediagrambelow.)Ateachmomentintimethe threepointscorrespondingtothedockandthepositionsofthetwopointsformatriangle.Is thetriangleformedafter10minutesoftravelsimilartothetriangleformedafter30minutesof travel?Explainthereasoningyouusedtoanswerthisquestiontoaclassmate. Boat Boat B10 B30 Dock min min Boat A10 min Boat A30 min 5. Aboyisrunningfromsecondbasetothirdbase.Ateachmomentintimeduringhisrun,the threepointscorrespondingtohisposition,thirdbase,andhomeplate,formatriangle.Locate thepointscorrespondingtohispositionaquarterofthewayand halfwaytothirdbase,and drawthetriangles.Arethetwotrianglessimilar?Explainyouranswertoaclassmate. 2ndBase 3rdBase HomePlate HIDOE Geometry SY 2016-2017 111 L12 – Dilations and Similarity 12.4 – Introduction to Similarity Name _____________________________ Per _____ Date _____________________ 6. Refer to the diagram shown below. A. Rotate DBCD 90° CW about point A. Dilate the image by a scale factor of 0.5 with center A. Label it DB ' C ' D ' C B D A B. Explain how you knew which vertices to label B’, C’, and D’. C. The image and pre-image are related, in that DBCD and DB ' C ' D ' are _____________________ . HIDOE Geometry SY 2016-2017 112 L12 – Dilations and Similarity 12.5 – Homework Name _____________________________ Per _____ Date _____________________ Complete the following rigid motion transformation and dilations to create new images of the given figures. 1. Rotate DEFG 90°CCWaboutpointAanddilatetheimagebyascalefactorof1.5,andlabelthe resultingimage DE ' F ' G ' . E F G A Check your work by measuring the corresponding angles: mÐE = _________ mÐE’ = _________ mÐF = _________ mÐF’ = _________ mÐG = _________ mÐG’ = _________ The image and pre-image are related, in that DEFG and DE ' F ' G ' are ____________________ . HIDOE Geometry SY 2016-2017 113 L12 – Dilations and Similarity 12.5 – Homework Name _____________________________ Per _____ Date _____________________ 2. Reflect DHIJ aboutlinem,translatetheresultingimageusingthetranslationdefinedbyT(x, y)=(x,y–5),anddilatetheresultingimagebyascalefactorof2abouttheleft-mostpointof thetriangle.Labeltheresultingtriangle DH ' I ' J ' . m H I J The image and pre-image are related, in that DHIJ and DH ' I ' J ' are ____________________ . HIDOE Geometry SY 2016-2017 114 L13 – Similar Triangles Name _____________________________ 13.1 – Looking Ahead: Using Similar Triangles to Solve Problems Per _____ Date ____________ Motivation:Attheendofthisunit,youwillbeabletosolvethefollowingproblems. Real-WorldProblem:Grandma needs to measure the palm tree in her front yard in order to have it removed by professionals. She is perplexed by this task since measuring the height of the tree with a tape measure is difficult, if not impossible. As the kids are playing in the yard, grandma notices the shadow her granddaughter casts on the ground looks to be in the same proportion to her height as the tree’s shadow on the ground is to the tree’s height. If her 5-foot tall granddaughter has a shadow 8-feet long, sketch a diagram to find the tree’s height if its shadow is 24 feet. Real-WorldProblem:Grandmaistakingoutarowofbushesalongthesideofthehouseinorder toextendhertriangularvegetablegarden,shownbelow.Shewantsthevegetablegardentobeas largeaspossible,butretainitstriangularshape.Sincethenewgardenwillrunalongthesideofthe house,shecanonlyextendthe8-footsidetobe18feet,andtheedgealongthehousewillbeparallel withthe9-footside.Sketchadiagramofgrandma’snewgarden. 18 feet 8 feet 9 feet Grandma’s House 14 feet HIDOE Geometry SY 2016-2017 115 HIDOE Geometry SY 2016-2017 116 L13 – Similar Triangles 13.2 – Characteristics of Similar Triangles Name _____________________________ Per _____ Date _____________________ SIMILARTRIANGLES:Investigatethecharacteristicsofsimilartriangles 1. UsingthediagramofDABCbelow,measurethesides,andlabeleachsidewithitslengthin centimeters. B C A 2. Inthespaceabove,usearulertoextend AB to AB' todoubleitsoriginallength.Dothe samefor AC to AC' .ConnectB’andC’,andmeasureeachsideofthelargertriangleand labelitslength. € € € € HIDOE Geometry SY 2016-2017 117 L13 – Similar Triangles 13.2 – Characteristics of Similar Triangles Name _____________________________ Per _____ Date _____________________ 3. Comparethelengthsof BC and B'C' .Whatdoyounotice?Explain. € € 4. Repeatthisprocess,triplingtheoriginalsidelengthsusingtheextendedpointsB”andC”, andhalvingtheoriginalsidelengthsusingthepointsB’’’andC’’’.Doeswhatyounoticed aboutthethirdsidestillholdtrue?Explain. 5. Usewhatyoudiscoveredtomakeaconjectureaboutcorrespondingsidesofsimilar triangles. Insimilartriangles,correspondingsides___________________________________________ _________________________________________________________________________________________ 6. Now,measurealltheanglesineachtriangle.Whatdoyounotice? 7. Usewhatyoudiscoveredtomakeaconjectureaboutthecorrespondinganglesofsimilar triangles. Insimilartriangles,correspondinganglesare_______________________________________. HIDOE Geometry SY 2016-2017 118 L13 – Similar Triangles 13.3 – Similarity and Proportion Name _____________________________ Per _____ Date _____________________ Part I: Follow your teacher’s instructions and use the space below to take guided notes. 1. Similar ( ~ ) Triangles (#VOC): corresponding angles are ___________, and corresponding sides are _________________________ (meaning the ratios of their lengths are __________). 2. Proportion (#VOC): a statement that two ratios are ________________. • For example, a b = c d (read as “________________________________________________”) a 3. Similarity Ratio (written as b ) (#VOC): the ratio of lengths of ____________________ sides; € always measured in the same ______________. 4. R Are the triangles€to the right similar? Y If so, write the similarity statement and state the similarity ratio. 2 4 6 X 3 12 Z Q 9 S 5. Extended Proportion: a statement that __________ or more ratios are ___________. (#VOC) 6. Write an “extended proportion” to show the equivalence between the ratios of all pairs of corresponding sides of DXYZ and DQRS. 7. If h i j Properties of Proportions k = , which of the following must be true? A.8x=5y x y = B. 5 8 y 8 = C. x 5 isequivalentto 1)ad=bc (Cross-ProductProperty) € HIDOE Geometry SY 2016-2017 € 2) 3) 119 L13 – Similar Triangles 13.3 – Similarity and Proportion Name _____________________________ Per _____ Date _____________________ 8. Determine the value of x that makes each statement true. A. 13 = 9. In the diagram, ΔART ~ ΔBUS . 𝟔 𝒙 B. j R = h C. l 8 𝑥 = 𝑥 2 T R mno = p kmno B A. Determine the similarity ration between DART and DBUS. B. What is the measure of ÐU? C. What is the length of 𝑆𝐵? D. What is the measure of ÐA? E. F. D. € S 10 cm 18 cm U 56° A 12 cm R What is the measure of ÐS? If the given similarity statement was written as ΔBUS ~ ΔART , how would that affect the similarity ratio? HIDOE Geometry SY 2016-2017 € 120 L13 – Similar Triangles 13.3 – Similarity and Proportion Name _____________________________ Per _____ Date _____________________ Part II: Practice exercises 10.If xy = 47 ,whichofthefollowingmustbetrue?Justifyyouranswer. A. x y = 4 7 B. x y = 7 4 C. x 12 = y 21 C. 3 5 = x x +1 € € 11.Solveforx. 7 5 x 3 A. = € € € 2 x B. = x 32 € 12.DVOC~DTMH.Findthevalueofthevariablesx&y. H V 10 in T 24in 8 in x y M C O 40 in HIDOE Geometry SY 2016-2017 121 HIDOE Geometry SY 2016-2017 122 L13 – Similar Triangles 13.4 – Homework Name _____________________________ Per _____ Date _____________________ Solve for x. 1. 9 12 = 24 x 2. € x 9 = 4 x 3. € 3. x +1 6x − 2 = 9 36 € ΔWXZ ~ ΔDFG Z G € 3 in W 37° 4 in 10 in X D 6 in F Determine each of the following: A. the similarity ratio B. m∠Z € C. m∠G € D. GF € E. m∠D € F. WZ € HIDOE Geometry SY 2016-2017 123 L13 – Similar Triangles 13.4 – Homework Name _____________________________ Per _____ Date _____________________ 5. Find the value of the variables if Δ𝑀𝑄𝐴~ΔEOD. O Q 108° 4m z 3m (2x+4)° A 9m M 6m y° (3x–14)° E D 6. The triangles below are similar. Determine the value of the variables x and y. 3 m. y 7 m. x HIDOE Geometry SY 2016-2017 5 m. 17 m. 124 L13 – Similar Triangles 13.5 – Theorems About Similar Triangles Name _____________________________ Per _____ Date _____________________ Part I: Investigate what information you need to prove two triangles are similar. Materials: - protractor - ruler 1. In DABC below, use a protractor to label ÐA with its measure (to the nearest degree). B C A 2. Using the line drawn below and a protractor or patty paper, create an angle congruent to ÐA from Question 1 at point R. Given this angle, attempt to draw a triangle that is not similar to DABC. S R 3. Were you able to draw a triangle not similar to DABC? Explain. HIDOE Geometry SY 2016-2017 125 L13 – Similar Triangles 13.5 – Theorems About Similar Triangles Name _____________________________ Per _____ Date _____________________ 4. Measure and label ÐB from Question 1. Again, create an angle congruent to ÐA at point K and an angle congruent ÐB at point L. Attempt to draw a triangle that is not similar to DABC. L K 5. Use what you discovered to make a conjecture about the minimum amount of angle measures needed to prove triangles similar. The minimum number of angle measures needed to prove triangles are similar is _________ sets of corresponding congruent angles. 6. If you have two sets of corresponding congruent angles in a triangle, what does that say about the last pair of corresponding angles? Explain. HIDOE Geometry SY 2016-2017 126 L13 – Similar Triangles 13.5 – Theorems About Similar Triangles Name _____________________________ Per _____ Date _____________________ Part II: Follow your teacher’s instructions and use the space below to take guided notes. àSimilarTriangles: 1)aretwotrianglesthathaveexactlythesame____________butNOTnecessarilythe same_____________. 2)occurwhencorresponding___________arecongruentANDcorresponding ______________areproportional. 3)showtheirrelationshipusinga_____________________________________,the ratioofthelengthsofcorresponding______________. Three Ways to Prove Two Triangles are Similar Without Relying on the Definition Angle-AngleSimilarityTheorem(AA~Postulate)(#THM) C A D O If______anglesofone______are_________to______angles G ofanother_________,thenthetwo__________are__________. Side-Angle-SideSimilarityTheorem(SAS~Theorem)(#THM) A Ifanangleofone______is______toanangleofanother______, andthesides____________________thetwoanglesare ________________________,thenthetwo________are______. T H 3 E 40° 2 40° T M G Side-Side-SideSimilarityTheorem(SSS~Theorem)(#THM) Ifthe___________________________sidesoftwo________are K N 24 6 16 _________________________,thenthetwo________are______. HIDOE Geometry SY 2016-2017 6 4 4 L 4 Q 1 P M 127 L13 – Similar Triangles 13.5 – Theorems About Similar Triangles Name _____________________________ Per _____ Date _____________________ PartIII:Practiceexercises 7. Is enough information provided to prove that the following triangles are similar? • If so, write the similarity statement and name the postulate or theorem you used. • If not, explain why not. A. B. U Y 8 Z 5 4 30° C V T R 6 X 10 8 30° A 12 B Q S 13 C. A 2 4 B Q 4 M 8 P 8. Each diagram contains 2 triangles that are similar. Determinethevalueofx. 42 A. 9 B. C. 12 15 17 10 x 8 x 5 x 6 12 14 HIDOE Geometry SY 2016-2017 128 L13 – Similar Triangles 13.5 – Theorems About Similar Triangles 9. 10. € € Name _____________________________ Per _____ Date _____________________ Lookingbackatgrandma’sgarden,tothenearestfoot,howmuchedgingwillgrandmaneed topurchasetomakeanewborderaroundherentirevegetablegarden? 18 feet 8 feet 9 feet 14 feet Justify the following statements using the similarity postulates or theorems. A. ΔABC ~ ΔADB B B. ΔABC ~ ΔBDC A D C C. ΔADB ~ ΔBDC € HIDOE Geometry SY 2016-2017 129 HIDOE Geometry SY 2016-2017 130 L13 – Similar Triangles 13.6 – Homework 1. Name _____________________________ Per _____ Date _____________________ Is enough information provided to prove that the following triangles are similar? A. • If so, write the similarity statement and name the postulate or theorem you used. • If not, explain why not. K N 3 J 70° M C. B. 20° L 6 S 110° B T R P 20° A 50° C Q A 40° 40° X B 2. A. 70° 2 4 R C Each diagram contains 2 triangles that are similar. Determinethevalueofx. B. C. 15 4 12 x 3 12 10 x x 7 11 8 4 8 HIDOE Geometry SY 2016-2017 131 L13 – Similar Triangles 13.6 – Homework 3. Name _____________________________ Per _____ Date _____________________ The figure below contains three similar triangles: DABC ~ DADB ~ DBDC B y 6 A A. x D 9 C In the given figure above, DADB and DBDC are embedded in DABC, making them a little difficult to see. The diagram below separates the 3 triangles to make them a little easier to distinguish from each other. Label the vertices of each of the 3 triangles below. To help you, use the given similarity statement and use any rigid motion transformations to help you figure out the corresponding vertices. B. Determine the values of x and y in the given figure above. HIDOE Geometry SY 2016-2017 132 L13 – Similar Triangles 13.7 – The Geometric Mean Name _____________________________ Per _____ Date _____________________ Grandma wants to put in a pool and Jacuzzi in the Northwest (back left side) corner of her back yard. She wants to be different and make both of them triangular shaped. She also wants to build them so that they share a common wall so people can easily climb from one to the other. See figure below. The common wall is an altitude for the larger triangle. Pool 4X Jacuzzi X Grandma knows she wants the hypotenuse of the pool and Jacuzzi together (the largest triangle) to be 40 ft. and that the Pool portion of the hypotenuse should be four times as long as the Jacuzzi portion of the hypotenuse. Help her find the rest of the measurements so she can buy the right amount of materials. 1. What kind of triangle is formed by the pool and Jacuzzi together? 2. What kind of triangles are the pool and Jacuzzi separately? 3. Determine the value of X and 4X. HIDOE Geometry SY 2016-2017 133 L13 – Similar Triangles 13.7 – The Geometric Mean Name _____________________________ Per _____ Date _____________________ In order for the contractors to lay out the pool and Jacuzzi, what they really need are the measurements along the property boundaries (i.e., the other two legs of the largest triangle). They will also need the length of the dividing wall. Before we find the remaining measurements for Grandma, let’s explore and make conjectures to help us. 4. Each larger triangle below contains two smaller inner triangles. For each set of three triangles thus formed, determine which of the three triangles are similar. Write similarity statements and explain why you think they are similar. E A 58° G 7.5 32° B C D 4.5 10 6 H 8 F 5. Make a conjecture about similarity of the three triangles determined by the altitude to the hypotenuse in a right triangle. HIDOE Geometry SY 2016-2017 134 L13 – Similar Triangles 13.7 – The Geometric Mean Name _____________________________ Per _____ Date _____________________ 6. Now let’s prove it! Given: Right ΔABC 𝐵𝐷 is an altitude for ΔABC 𝑚∠𝐴𝐵𝐶 = 90∘ Prove: ΔABC~ΔADB~ΔBDC Statement Reason 7. Theorem 19.4: The altitude to the hypotenuse of a right triangle forms _________ triangles that are similar to _______________________ and ________________________. (#THM) 8. Use Theorem 19.4 to find the missing labeled lengths in the triangles below. HIDOE Geometry SY 2016-2017 135 L13 – Similar Triangles 13.7 – The Geometric Mean Name _____________________________ Per _____ Date _____________________ R Y 4 C S x 5 16 T x 12 Z X Q 9. What do you notice about the proportions you made within the last two triangles? Geometric mean: x is the geometric mean between positive numbers p and q if and only iff p x = . x q This is equivalent to pq = x 2 . (#VOC). Why do they call this the Geometric Mean? • The Arithmetic mean of two numbers is their midpoint (add them together and divide by 2). • To find the Geometric mean you multiply them together and find their positive square root. HIDOE Geometry SY 2016-2017 136 L13 – Similar Triangles 13.7 – The Geometric Mean Name _____________________________ Per _____ Date _____________________ Example:Determinethegeometricmeanof3and12 t h h oR = 𝑥 R = 36 𝑥 = 6 10. Practicefindingthegeometricmeanofthefollowingnumbers. A.3,27 B.20,5 11. Given:RightΔABCandaltitude𝐵𝐷 Statement `c ac Prove: = ac C.6,8 Reasoning cb A D B C HIDOE Geometry SY 2016-2017 137 L13 – Similar Triangles 13.7 – The Geometric Mean Name _____________________________ Per _____ Date _____________________ 12. Theorem13.7:Thealtitudetothehypotenuseofarighttriangleisthe_________________________ ________________________ofthetwosegmentsintowhichitdividesthehypotenuse.(#THM). Let’s try to make sense of this theorem. Referring to the diagram in the proof for the previous problem (question #11): • Imagine if you copy 𝐴𝐶 from the diagram and use it form a rectangle such that 𝐷𝐶 is perpendicular to 𝐴𝐷. o The area of this rectangle would be the product of lengths of those 2 sides of the rectangle: Area = (𝐴𝐷)(𝐷𝐶). A A D D C B • C Now, look at the altitude of the triangle (i.e., 𝐵𝐷 ) and picture a square with each side having a length of 𝐵𝐷 . o The area of this square would be the length of 𝐵𝐷 squared: Area = (𝐵𝐷)(𝐵𝐷). B D • Therefore, one way to interpret what Theorem 13.7 means is, “The area of the rectangle formed by the two segments in the hypotenuse of the triangle is equal to the area of square formed by the altitude of the triangle.” • This relationship is a reason the altitude of a triangle is can be referred to as the Geometric Mean. HIDOE Geometry SY 2016-2017 138 L13 – Similar Triangles 13.7 – The Geometric Mean Name _____________________________ Per _____ Date _____________________ 13. Now let’s return to Grandma’s pool/Jacuzzi. Using the theorems we just proved, together with other facts you know about right triangles, determine all the missing lengths for her pool and Jacuzzi. Hint: determine the value for h first. X Pool Y h = _____________ X = _____________ Y = ____________ HIDOE Geometry SY 2016-2017 139 HIDOE Geometry SY 2016-2017 140 L14 – Similarity and Proportionality 14.1 – Construction Warm-up Name _____________________________ Per _____ Date _____________________ The Great Gazebo Project: Grandma is thinking ahead to her days of leisure, sitting in her Gazebo and watching her grandkids play, sipping on iced tea. As a helpful grandson you volunteer to help her with some of the planning, while your sister has offered to do most of the actual work. Before you start though, she wants to be sure you remember your geometry. After all, how can you be trusted to modify blueprints and calculate distances if you can’t even bisect a line or angle! Grandma’s First Day Challenge! Completethesimpletasks belowtoprovethatyou knowyourstuff. Using a compass and straightedge, or patty paper, construct the following on the next page: 1. Draw a Line Segment and draw its Perpendicular Bisector. 2. Draw a line and a point not on the line, and then draw another line that is Parallel to the first line passing through the point. 3. Draw an Acute Angle and Bisect it. 4. Construct an Equilateral Triangle HIDOE Geometry SY 2016-2017 141 L14 – Similarity and Proportionality 14.1 – Construction Warm-up Name _____________________________ Per _____ Date _____________________ 1. 2. 3. 4. HIDOE Geometry SY 2016-2017 142 L14 – Similarity and Proportionality 14.2 – The Altitude and Mean Name _____________________________ Per _____ Date _____________________ Project 1: Your first project is to help Grandma with two windows she has chosen to add into her house. Both options she has chosen are triangular and will be located using the orientations shown below. She wants to know which is taller, but the manufacturer only lists the area of the glass and the length of each side. She needs the Altitude of each window. (#VOC) Altitude of a Triangle: The Line Segment containing a designated vertex that is perpendicular to the line containing the opposite side. Note: Since each triangle has three vertices, each triangle has exactly three altitudes. Two possible window designs are shown below: Task A: Construct the altitude of the glass window pane shown below, using the highest point as the vertex from which the altitude is drawn. Task B: Construct the altitude of the glass window pane shown below, using the highest point as the vertex from which the altitude is drawn. This may appear to be more difficult, since the altitude is drawn outside the triangle. But remember, the altitude is drawn to the line containing the opposite side, so simply extend the base of the window prior to drawing the altitude. HIDOE Geometry SY 2016-2017 143 L14 – Similarity and Proportionality 14.2 – The Altitude and Mean Name _____________________________ Per _____ Date _____________________ Project 2: We also need to cut each window in half (for some reason, perhaps the glass is too large and needs to be supported in the middle). For symmetry, each half must have the same area. If we find the median of the base of the triangle and connect that point to the opposite vertex, it will create two new triangles that have the same height (as determined by the common vertex) and the same base (half the original), and hence the same area. This line is called the Median of a Triangle. (#VOC) Median of a triangle: The Line segment that extends from a designated vertex to the midpoint of the opposite side. Note: Each triangle has exactly three medians. Task A: Construct the Median containing the highest point, for the glass pane shown below. Task B: Construct, using dotted lines, the Altitudes for the two smaller triangles you just created with the median. Include the highest point on each smaller triangle in each altitude. How many dotted lines did you draw? What does this imply about the areas of the two smaller triangles? HIDOE Geometry SY 2016-2017 144 L14 – Similarity and Proportionality 14.3 – The Mid-segment Theorem Name _____________________________ Per _____ Date _____________________ Objective: To find proportional lengths formed by the mid-segment in triangles and trapezoids. Grandma is finally working on finishing touches for her house, and realizes she needs more storage. She wants to include a shelf in the attic that is located halfway up the triangular wall at the end of the attic. How can she determine where to put the shelf? How long should she make the shelf? MID-SEGMENT (A __________ that joins the __________ of two segments) #VOC 1. Draw and cut out a large scalene triangle. Each member should have a different kind of triangle (right, acute, and obtuse triangles). Label your vertices A, B, and C. 2. Find and mark the midpoint of 𝐴𝐶 by folding A onto C. Find and mark the midpoint of 𝐵𝐶 in the same way. Label the midpoints D and E correspondingly, and draw 𝐷𝐸. C A B C D A E B 3. Fold your triangle on𝐷𝐸. A B 4. Fold A to C. Do the same for B. B 5. a) What type of quadrilateral does the folded triangle appear to form? b) What does this tell you about 𝐷𝐸 and 𝐴𝐵? Explain. 6. What conjecture can you make about how the mid-segment of a triangle is related to the third side of a triangle? HIDOE Geometry SY 2016-2017 145 L14 – Similarity and Proportionality 14.3 – The Mid-segment Theorem Name _____________________________ Per _____ Date _____________________ Theorem14.1:TriangleMid-segmentTheorem Ifasegmentjoinsthe________________of______sidesofa ____________,thenthe________________is________tothe A S K ________________sideand____________itslength.#THM C B Example1:𝐷𝐸and𝐸𝐹aremidsegments.DE=7andAB=10. a)FindAC. B E D b)FindEF. C c)WhatistheperimeterofADEF? A F Example2:Simoneisdesigningakiteforacompetition.Sheplanstouseadecorativeribbonto connectthemidpointsofthesidesofthekite.Thediagonalsofthekitemeasure 64cmand90cm.Findtheamountofribbonshewillneedtobuy. HIDOE Geometry SY 2016-2017 146 L14 – Similarity and Proportionality 14.3 – The Mid-segment Theorem Name _____________________________ Per _____ Date _____________________ àMid-segmentofatrapezoid:a__________________thatjoinsthe the______________ofthe___________________sidesofa________________.#VOC Theorem14.2:TrapezoidMid-segmentTheorem Themid-segmentofatrapezoidis_______________tothe basesandhalfaslongasthe_____________ofthelengths ofthe____________________.#THM Example3:𝐷𝐸isthemid-segmentofthetrapezoidQRST. a) 𝐷𝐸 is parallel to _____ and ______ T R M S P A Q R D E T S b) If QR = 14 and ST = 7, then DE = _______ c) If DE = 7 and ST = 11, then QR = _______ d) If DE = 2x+3, QR = 7x–2, and ST = 3x–10, then QR = _______ Example4:LayerCake.Abakerismakingacakeliketheoneatthe right.Thetoplayerhasadiameterof8inchesandthe bottomlayerhasadiameterof20inches.What shouldthediameterofthemiddlelayerbe? HIDOE Geometry SY 2016-2017 147 HIDOE Geometry SY 2016-2017 148 L14 – Similarity and Proportionality 14.4 – Homework Name _____________________________ Per _____ Date _____________________ For1–5,intriangleABC,thepointsD,E,andFaremidpoints. 1. 𝐷𝐸 is parallel to ____________ F D 2. 𝐹𝐸 is parallel to ____________ 3. If AB = 14, then EF = ____________ A B C E 4. If DE = 6, then AC = ____________ M For6–9,intriangleMNO,thepointsX,Y,andZaremidpoints. 5. If YZ = 3x+1 and MN = 10x–6, then YZ = _____________ X Z O 6. If YX = x–1 and MO = 3x–7, then MO = _____________ Y N 7. If mÐMON = 48°, then mÐMZX = _____________ 8. If mÐMXZ = 37°, then mÐMNO = _____________ HIDOE Geometry SY 2016-2017 149 L14 – Similarity and Proportionality 14.4 – Homework Name _____________________________ Per _____ Date _____________________ Quadrilateral ABCD is a trapezoid with midsegment 𝐸𝐹. A B E F D C 9. If mÐB = 73°, then mÐC = ________________ 10. If AB = 28 and DC = 13, then EF = ________________ 11. If EF = 13 and DC = 6, then AB = ______________ 12. If DC = x+5 and DC + AB = 4x+6, then EF = ______________ HIDOE Geometry SY 2016-2017 150 8 L14 –CB Similarity = 2.48 cmand Proportionality 14.5 –ACUsing to Find Coordinates = 4.96Proportionality cm AC Name _____________________________ Per _____ Date _____________________ 7 Question:= How 2.00 do we find the coordinates of point C in the diagram below, if we know that C lies on CB line segment 𝐴𝐵 and is located 2/3 of the way from A to B? In general, how do we find the coordinates 6 A: (3.00, 1.03) of C if we know that C lies on 𝐴𝐵 and the ratio `b `a = 𝑝, where 0 < p < 1? 5 B 4 3 C 2 1 2 A 2 4 6 8 10 12 14 1 Let's investigate, by starting off with some easier examples. We will return to solve the problem above later in the lesson. 2 1. Find the coordinates of the point C that lies on the line segment AB below such that: 3 a. b. c. d. `b `a `b `a `b `a `b `a = o = o = t = v R t v 4 Coordinates for C = ________________ 5 Coordinates for C = ________________ 6 Coordinates for C = ________________ 7 Coordinates for C = ________________ j 8 9 HIDOE Geometry SY 2016-2017 151 L14 – Similarity and Proportionality 14.5 – Using Proportionality to Find Coordinates Name _____________________________ Per _____ Date _____________________ 2. FindthecoordinatesofthepointCthatlieson𝐴𝐵belowsuchthat: `b t a. = CoordinatesforC=________________ `a b. `b `a c. `b `a l o = R o = j CoordinatesforC=________________ CoordinatesforC=________________ 3. FindthecoordinatesofthepointCthatlieson𝐴𝐵belowsuchthat: a. b. `b `a `b `a c. `b `a d. `b `a o = CoordinatesforC=________________ R = CoordinatesforC=________________ CoordinatesforC=________________ CoordinatesforC=________________ R t t = v t = j HIDOE Geometry SY 2016-2017 152 L14 – Similarity and Proportionality 14.5 – Using Proportionality to Find Coordinates Name _____________________________ Per _____ Date _____________________ 4. FindthecoordinatesofthepointCthatlieson𝐴𝐵belowsuchthat: `b o a. = CoordinatesforC=________________ `a b. `b `a c. `b `a R R = . j l = k CoordinatesforC=________________ CoordinatesforC=________________ 5. Let'strytogeneralizethislastsituation.Supposenowthatpisanumberstrictlybetween0 `b and1.FindthecoordinatesofthepointCthatlieson𝐴𝐵abovesuchthat = 𝑝. HIDOE Geometry SY 2016-2017 `a 153 L14 – Similarity and Proportionality 14.5 – Using Proportionality to Find Coordinates Name _____________________________ Per _____ Date _____________________ Thelastsetofproblemswasrelativelyeasybecausethelinesegmentswereeitherhorizontalor vertical,whichmeantonecoordinatewasalreadydetermined,leavingyoutoonlyneedtofindthe othercoordinate.Wenowmovetonon-verticallinesegmentswithanon-zeroslope.Let'sbegin withthestartingpointAattheorigin. Example1:FindthecoordinatesofthepointC,locatedon𝐴𝐵belowsuchthat `b `a o = . R o Solution:ClearlyΔ𝐴𝐶𝐸issimilartoΔ𝐴𝐵𝐷.Itthenfollowsthatif𝐴𝐶 = 𝐴𝐵(whichwasgiven)it o o R R R mustfollowthat𝐴𝐸 = 𝐴𝐷and𝐶𝐸 = 𝐵𝐷.Thisisexactlythetechniqueweusedforourprevious horizontalandverticallinesegments,respectively.SinceAD=6andBD=3itfollowsthatAE=3 andBD=3/2,whichimpliesC=(3,3/2),whichwecouldhaveguessedfromthediagram. 6. FindthecoordinatesofthepointCthatlieson𝐴𝐵abovesuchthat: `b o a. = CoordinatesforC=________________ `a b. c. `b `a `b `a d. e. f. `b `a `b `a `b `a t R = CoordinatesforC=________________ o = CoordinatesforC=________________ = . CoordinatesforC=________________ o = CoordinatesforC=________________ t = . CoordinatesforC=________________ t v t v j j HIDOE Geometry SY 2016-2017 154 L14 – Similarity and Proportionality 14.5 – Using Proportionality to Find Coordinates Name _____________________________ Per _____ Date _____________________ Example2:FindthecoordinatesofthepointC,locatedon𝐴𝐵below,suchthat `b `a o = . t o Solution:Justasbefore,clearlyΔ𝐴𝐶𝐸issimilartoΔ𝐴𝐵𝐷.Itthenfollowsthatif𝐴𝐶 = 𝐴𝐵(which o o t t t wasgiven)itmustfollowthat𝐴𝐸 = 𝐴𝐷and𝐶𝐸 = 𝐵𝐷.SinceAD=7andBD=4,itfollowsthat AE=7/3andCE=4/3.What'sdifferenthere,incomparisontoExample1,isthatthesearenotthe coordinatesofC,thesearethesegmentlengths. InordertofindthecoordinatesofCwemustaddtheselengthstothecoordinatesofA.So,thexl v v o coordinateforCis−1 + = ,andthey-coordinateforCis−1 + = ,whichisconsistentwith t t thecoordinatesforConthegraph. t t 7. FindtheexactcoordinatesofthepointCthatlieson𝐴𝐵abovesuchthat: `b o a. = CoordinatesforC=________________ `a b. c. `b `a `b `a d. e. f. `b `a `b `a `b `a l v = CoordinatesforC=________________ o = CoordinatesforC=________________ = CoordinatesforC=________________ o = CoordinatesforC=________________ R = CoordinatesforC=________________ l R t v j j HIDOE Geometry SY 2016-2017 155 L14 – Similarity and Proportionality 14.5 – Using Proportionality to Find Coordinates Name _____________________________ Per _____ Date _____________________ 8. Returntotheproblemattheverybeginningofthelessonandfindtheexactcoordinatesofthe `b R `b pointCthatlieson𝐴𝐵suchthat = ,andmoregenerallythecasewhere = 𝑝for `a 0<p<1. t `a Hintforthefollowingproblem:EventhoughΔ𝐴𝐵𝐷isnotdrawnin,asinthepreviousexamples, youmaywishtoincludeitinordertovisualizethesimilarityproperty. 9. FindtheexactcoordinatesofthepointCthatlieson𝐴𝐵abovesuchthat: `b o a. = CoordinatesforC=________________ `a b. c. `b `a `b `a R R = CoordinatesforC=________________ l = CoordinatesforC=________________ = CoordinatesforC=________________ = CoordinatesforC=________________ CoordinatesforC=________________ t k d. e. f. `b `a `b `a `b `a t = v o ow p ow HIDOE Geometry SY 2016-2017 156 L14 – Similarity and Proportionality 14.6 – Parallel Lines in Triangles (Warm-up) Name _____________________________ Per _____ Date _____________________ Attic Shelves Grandma is thinking of building a set of 4 shelves along one end of the attic. (See dotted line shelves in the sketch below.) Y=20ft. X=30ft. She knows the attic floor is level and she wants to make sure her shelves are level. She already knows the lengths X & Y of her roof. What she wants to know is if she can just divide each of these by 5, mark those lengths on the side walls and connect the two points on each side with a line (the dotted lines). She can then follow the line when she puts up the shelf supports. Label each section of the roof in terms of X or Y. One section has been done for you. We ask some preliminary questions below, and will return to answer this question, in full, later in the lesson. 1. Do you think this would work? Why or why not? Discuss your thoughts with a classmate. 2. She can also check the heights along the line from each shelf below to make sure it is the same along the entire run of the shelf. How do you think Grandma could most easily determine the desired height from the base to the first shelf? Discuss your ideas with a classmate. HIDOE Geometry SY 2016-2017 X Y 157 HIDOE Geometry SY 2016-2017 158 L14 – Similarity and Proportionality 14.7 – Parallel Lines in Triangles Name _____________________________ Per _____ Date _____________________ Let’s experiment with several triangles to make conjectures that may help us with Grandma’s attic shelves. 1. For each scalene triangle below, determine the missing lengths, then write ratios to compare. L LN=18 Q 15 LM=____ 10 6 R T M K P QP=14 6 5 10 S N J KJ = LJ MN = LN KJ = LK MN = LM LM = LN LK = LJ SQ = QT RQ = QP ST = QT PR = QP SQ = TS RQ = PR 2. What do you notice about the ratios? 3. Corresponding lengths are ____________________. 4. How could we have determined the value for LM even if we were NOT given the value for LN, and similarly for PR if we were NOT given QP? Hint: The next question may help you answer this question. 5. How do you know DNJL 6. DMKL without using the fact that LN = 18? KM = ________ JN HIDOE Geometry SY 2016-2017 159 L14 – Similarity and Proportionality 14.7 – Parallel Lines in Triangles Name _____________________________ Per _____ Date _____________________ In the triangle below, using a straightedge and compass draw line l parallel to line segment AC passing through the midpoint D of side AB and intersecting side BC at E. Notice that by design, l divides side AB into two line segments with equal length AD and DB . 7. Discuss with your partner how you know that DDBE is similar to DABC . 8. Use a compass or ruler to check if l also divides BC evenly; that is, BE = EC. Discuss with your partner why this must be true. 9. Using a straightedge and compass, draw the altitude from B to AC . Discuss with your partner why l must also divide this perpendicular line segment into two line segments of equal length. 10. Repeat the process above, locating point D ¼ of the way from A to B. Explain why the line parallel to AC passing through D must also divide BC into two line segments of the same proportion. HIDOE Geometry SY 2016-2017 160 L14 – Similarity and Proportionality 14.7 – Parallel Lines in Triangles Name _____________________________ Per _____ Date _____________________ Reflection: If a line segment within DABC connects the midpoint on side AB with a point on side BC in such a manner that it is parallel to the base AC , then the endpoint on side BC must be its ________________________________________. Using the same reasoning as for the midpoint, if a line segment within DABC connects sides AB and BC in such a manner that it is parallel to the base AC , then it cuts the two sides ________________________________________. 11. Given: ΔABC and 𝐷𝐸 || 𝐴𝐶 Prove: `c ca = bx xa (*Hint: first prove similar triangles) Statement Reasoning 1) 1) Given 2) 2) Corresponding Angles 3) 3) Corresponding Angles 4) 4) 5) ΔABC ~ ΔDEB 5) 6) 7) 8) `a ca = ba ca `c ca = = bx xa D A E C 6) xa `ayca B bayxa xa 7) 8) From this proof we can state the following theorem: Theorem 14.3: If a line (or line segment) parallel to one side of a triangle intersects the other two sides, then it divides the other two sides _____________________. (#THM) Further, the length of this parallel line segment is __________________ to the length of the parallel third side. HIDOE Geometry SY 2016-2017 161 L14 – Similarity and Proportionality 14.7 – Parallel Lines in Triangles Name _____________________________ Per _____ Date _____________________ 12.UseTheorem14.3(onthepreviouspage)tohelpyousolvethefollowingproblem. Given𝐽𝐾||𝑌𝑍,solveforx. X 4 J 4 K6 x Y Z 4 13. WritetheconverseofTheorem14.3(#THM) Ifalinedividestwosidesofatriangle________________________________________,thenitis ________________________________________tothethirdsideofthetriangle. 14. UsingtheconverseofTheorem14.3(thatyoujuststatedabove), • identifyifthesegmentinsideofeachtriangleisparalleltothebase; • ifitisparallel,solveforx. A. B. Parallel?____________ Parallel?____________ x=__________ x=__________ HIDOE Geometry SY 2016-2017 162 L14 – Similarity and Proportionality 14.8 – Medians and Altitudes in Similar Triangles Name _____________________________ Per _____ Date _____________________ MediansinSimilarTriangles 1. Recallthatthemedianconnectsa_______________tothe__________________ontheoppositesideofa triangle.Drawtheremainingtwomediansinthetrianglebelow. Z Y M X 2. Giventhateachpairoftrianglesbelowissimilar,withamediandrawnin,fillinthemissing lengthsandwritetheratiooftheirsidesandoftheirmedians. 𝑌𝑍 Z = 𝐴𝑇 𝑍𝑀 = 𝑇𝑃 T 12 𝑍𝑀 = 𝑌𝑍 𝑇𝑃 = 𝐴𝑇 Y M 3 YM=_____ 𝐸𝐿 = 𝑇𝐴 𝐸𝑀 = 𝑇𝑃 8 X 3 A 6 2 6 C P T E 10 𝑇𝑃 = 𝑇𝐶 𝐸𝑀 = 𝐸𝐹 9 9 6 5 4 3 HIDOE Geometry SY 2016-2017 8 L 1 M F A P 2 C 163 L14 – Similarity and Proportionality 14.8 – Medians and Altitudes in Similar Triangles Name _____________________________ Per _____ Date _____________________ 3. Makeaconjectureabouttheratiosofmedianstocorrespondingsidesinsimilartriangles. 4. Nowlet’sproveit. B Given:ΔABC~ΔXYZ 𝐵𝑀and𝑌𝑁aremedians C A M `a a• Y Prove: = •€ €‚ *Hint:Usesimilartriangletheorems. X N Z Statement Reason 5. Theorem14.4:Correspondingmediansofsimilartrianglesare___________________tothe corresponding___________________.(#THM) HIDOE Geometry SY 2016-2017 164 L14 – Similarity and Proportionality 14.8 – Medians and Altitudes in Similar Triangles Name _____________________________ Per _____ Date _____________________ Useknowntheoremstohelpyousolvethefollowingproblem. 6. ΔOLA~ΔFET,solveforx. F O 20 12 15 9 M L 16 x A E C T AltitudesinSimilarTriangles 7. Eachpairoftrianglesbelowissimilar.Usearulertofindtheratiosofcorrespondingsidesand thealtitudeswithineachtrianglepair. A C D C B X O G A T Z Y 8. Whatdoyounoticeabouttheratiosbetweencorrespondingsidesandtheratiobetween altitudesforeachsimilarpair? HIDOE Geometry SY 2016-2017 165 L14 – Similarity and Proportionality 14.8 – Medians and Altitudes in Similar Triangles Name _____________________________ Per _____ Date _____________________ 9. WhymustthisbetrueforALLpairsofsimilartrianglesandtheiraltitudes?Whatprevious theoremsorpostulatesgiveevidenceofthis? 10. Useyourexplanationinthepreviousproblemtohelpyouwiththefollowingproof. A Given: ΔABC~ΔXYZ 𝐴𝑃and𝑋𝑆arealtitudes Prove: `a •€ = ab €ƒ = `b •ƒ = `d •„ B C P X Y Statement S Z Reason 11. Theorem14.5:Correspondingaltitudesofsimilartrianglesare_________________________________ tothecorresponding_________________________________.(#THM) HIDOE Geometry SY 2016-2017 166 L14 – Similarity and Proportionality 14.8 – Medians and Altitudes in Similar Triangles Name _____________________________ Per _____ Date _____________________ 12. Restatingthe4resultsfromthelasttwolessons: • Ifalineparalleltoonesideofatriangleintersects________________________,thenitdivides ________________________________________________________________. • Ifalinedividestwosidesofatriangle__________________________,thenitis ___________________________________________________________ofthetriangle. • Corresponding__________________ofsimilartrianglesare____________________tothe correspondingsides. • Corresponding__________________ofsimilartrianglesare____________________tothe correspondingsides. 13. Usetheaboveresultstofindthemissingmeasuresinthefiguresbelow.Assumepairsof trianglesaresimilar. a) B b) 10 8 15 6 E D 20 ? ? 4 A C c) ? 6 3 4 3 4 HIDOE Geometry SY 2016-2017 167 L14 – Similarity and Proportionality 14.8 – Medians and Altitudes in Similar Triangles Name _____________________________ Per _____ Date _____________________ 14. Grandmadecidesthattheeasiestwaytodeterminethedistancebetweenheratticshelvesisto measurethealtitude,fromthepeakofherrooftothefloor,anddividethatdistanceby5(why 5andnot4,sincethereare4shelves?).Shecanthenmarkthisdistanceatvariouslocations acrosstheatticendwallwheretheshelveswillbelocated,measuringfromthefloor,then connectthedotsandformaguideforthebottomshelf.Shecanthencontinuethisforthe secondshelf,measuringfromthefirstshelf,etc.,untilshearrivesatthelastshelf.Discusswith yourpartnerwhythisworks,sightingappropriateresultsfromthelasttwolessons,andwrite yourexplanationbelow. 15. Supposetheceiling(i.e.thebottomofthemaintriangle)is25ft.HowlongwillGrandmaneed tocuteachshelf?Supposeinsteadthattheceilinglengthis24ft.HowlongwillGrandmaneed tocuteachshelfinthisinstance? X Y HIDOE Geometry SY 2016-2017 168 L14 – Similarity and Proportionality 14.9 – Homework Name _____________________________ Per _____ Date _____________________ 1. Findthemissingvaluesbelow. X=____________ Y=____________ 2. Findthemissingvaluesbelow. X=____________ Y=____________ HIDOE Geometry SY 2016-2017 169 L14 – Similarity and Proportionality 14.9 – Homework Name _____________________________ Per _____ Date _____________________ 3. Findthemissingvaluesbelow,giventhat∆𝐴𝐵𝐶~∆𝐴… 𝐵… 𝐶 … . W=____________ X=____________ Y=____________ 4. Findthemissingvaluesbelow,giventhat∆𝐴𝐵𝐶~∆𝐴… 𝐵… 𝐶 … . X=____________ Y=____________ W=______________ Z=_______________ HIDOE Geometry SY 2016-2017 170