* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download 7.1 Measurement of Angles
Survey
Document related concepts
Transcript
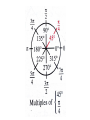
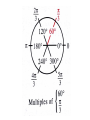
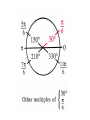
7.1 Measurement of Angles -If you leave this class with anything this year, it will be a better understanding of sine/cosine/tangent and angle measurments • In trigonometry an angle often represents a rotation about a point. " theta " Initial Ray A common unit for measuring angles is the revolution, a complete circular motion. The unit for measuring smaller angles is degrees, of which there are 360 degrees in one complete revolution. • There are 2 ways that degrees can be expressed they can be written in decimal form or they can be written with degrees/minutes/seconds When measuring an angle and it falls between two whole number degrees and we simply do not want to round that value we can be more precise with our measurement and break 1 degree down into 60 minutes, and then break 1 minute down into 60 seconds. Here is the notation. o 74 32 ' 45'' Often we like to convert between these 2 different forms. • To convert decimal degrees into degree/minute/seconds – Subtract away your whole number degree • Multiply remaining decimal by 60, then take the resulting value, subtract away the whole number and that whole number is your minute value. • With the resulting decimal from the previous step multiply that decimal by 60 and the resulting whole number is your seconds value. – Round your seconds for this class. 39.452 o Going from minutes/seconds to decimal • Take your degree value and put that to the left of your decimal. • Take your minute part and divide by 60. • Take your second part and divide by 3600 • Sum the previous three decimals and you now have a decimal degree equivalent to the minute/second format o 39 27 '7 '' • We know of one unit of measuring angles and that is through the use of degrees. A second unit is called RADIANS. (remember the mode button on your ti83/84s?) • Here is a comparison, we can measure the distance between two objects in terms of feet or we could measure the distance in terms of meters. Both provide valid measurements but the values are completely different. • Degrees and Radians are the same way, they both measure the same thing (an angle) but the values are completely different yet both valid. Radians seem difficult to use initially because they are relatively new to us they are something we have never dealt with before • When an arc of a circle has the same length as the radius of the circle the measure of the central angle is then 1 radian. Basically we want to think of how many radiuses can fit into the arc, and that tells you how many radians the central angle is. • Radian measure of the central angle is the number or radius units in the length of the intercepted arc. Hence the name RADIAN • So now if the central arc is theta it can be measured by taking the arc length and dividing it by the radius length. s arc length r radius • If we think about the entire circle and want to know the measurement of the entire circle in terms of radians, we look at the circumference. We know the C=2πr thus the arc of the entire circle would be 2πr. We also know that the radius of any circle can be shown as r. s 2 r so now 2 r r • So one entire revolution around the circle would be 2π radians. So now we can make the argument that 360⁰=2π radians. 180⁰= π radians This allows for the 2 following conversion formulas: 1 radian 1deg ree 180o 180 o deg rees radians We can now convert radians into degrees and degrees into radians (much like we convert other measurements) • Helpful hint, in converting these 2 units you always want the initial units to disappear, thus the conversion rate that you multiply by must have that unit in the denominator. The only 2 numbers we use in our conversions are 180⁰ and π. • CONVERT THE FOLLOWING o 325 152 o 3.2 radians 2 radians 3 Angle measurements that can be expressed in degrees as whole numbers cannot be expressed in radians as whole numbers and vice versa. Therefore most of the time radians are given as fractional parts of π. The following 3 slides provide the angle measurements that we use most frequently they will be presented in degrees and radians. It is essential that you memorize these, you will be quizzed on them frequently Now all together as one Tomorrow I will teach a quick and easy way to remember how to reproduce this picture. • When an angle is shown in the Cartesian plane it is usually shown in standard position. Which means that the angles vertex is at the origin and its initial ray is along the positive x axis. • The terminal ray may move counterclockwise (initially up) and the angle is referred to as being positive. • If the terminal ray moves clockwise (initially down) then the central angle is referred to as being negative. • Show examples on the board • Sometimes we can place two angles on the same coordinate plane. If both angles are in standard position and they have the same terminal angle, then the angles are said to be COTERMINAL. For example and angle of 20⁰ and 380⁰ would have the same terminal ray, therefore they would be coterminal. • An angle of π/4 and 9π/4 would be coterminal • Identifying coterminal angles in degrees – Initial angle + k360⁰ (where k is the number of revolutions) • Identifying coterminal angles in radians. – Initial angle + k2π • Find 2 coterminal angles of degrees 2 in radians and 3 Homework pg. 261 3-8, 11, 13, 14, 17-19