Download Traveling on a Rotating Sphere

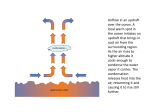
Ocean Motion
Teacher Guide
Lesson
2
Traveling on a Rotating Sphere
Cold are the feet and forehead of the earth,
Temperate his bosom and his knees,
But huge and hot the midriff of his girth,
Where heaves the laughter of the belted seas,
Where rolls the heavy thunder of his mirth
Around the still unstirred Hesperides.
The Belted Seas, Arthur Colton
http://earthobservatory.nasa.gov/Newsroom/BlueMarble/BlueMarble_2002.htm
Ocean Motion
Teacher Guide
Lesson
2
1
Lesson Objectives
Performance Tasks
To demonstrate an understanding of
convection
Using a model of heating water on a stove, propose an
explanation for the behavior of the movement of water.
Predict how this applies to fluids moving on or near the
Earth’s surface.
Observe an animation of the rotating Earth and draw
conclusions about the speed of objects at different
latitudes.
To demonstrate an understanding of
how a rotating sphere affects speed
at different locations
To demonstrate an understanding of
variables that affect circular motion
To demonstrate an understanding of
the Coriolis force and how it affects
the trade winds
Predict the effect of radius and speed on the tension of
a string connected to an object in circular motion.
Relate these predictions to the formula for centripetal
acceleration.
Use an online visualizer to generate trajectories on the
surface of a smooth Earth-like sphere. Judge if each
trajectory follows Coriolis’s rules.
To demonstrate an understanding of
how Coriolis acceleration varies with
latitude
Use the online visualizer to generate trajectories on the
surface of a smooth Earth-like sphere. Find the pattern
of change in the strength of the Coriolis force with
latitude.
Materials:
Student Guide (PDF file)
Internet access
Grade Level: high school
Time: 50 minutes
Courses supported: Earth Science, Physics, Math
Glossary: centripetal force, convection, Coriolis force, El Niño, Equator, Hadley cell, latitude,
and trade winds
Introduction: Spin-offs on a Rotating Sphere
The ocean and atmosphere are in constant motion.
Powered by the Sun and a rotating Earth, their
interactions play a critical role in shaping weather and
climate. Natural variations in winds, currents, and
ocean temperatures can temporarily affect weather
patterns. For example, an El Niño event may develop
when the trade winds diminish. The trade winds also
affect ocean travel today as well as in the past when
they aided early explorers and merchants traveling
from Europe to the Americas. The trade winds are a
pattern of wind found in bands around the Earth's
equatorial region. They are the prevailing winds in the
tropics, blowing from the high-pressure area in the
horse latitudes towards the low-pressure area around
the equator. The constancy of the trade winds makes
them important phenomena to be studied. What
causes these winds near the Equator and who
developed the concepts that explain them?
Lesson 2 will guide you through the history of scientists such as George Hadley, Edmond Halley
and Gaspard-Gustave de Coriolis, who developed the early concepts that explain the forces
powering the trade winds and their effect on ocean surface currents. Lab experiments and
computer models, found in this lesson, will help you understand these forces that influence the
weather and climate that you experience everyday.
Ocean Motion
Teacher Guide
Lesson
2
2
Engage: Preconceptions Survey, “What do you know?”
Students are asked to take an online
consisting of seven questions. When they
submit their responses online, a pop-up window appears that shows the correct response to
each question and provides additional, clarifying information all seven questions, the correct
responses, and additional information are provided below.
Engagement activities such as this one are typically not graded. Student responses to this
survey will help determine how much accurate information they already know about the
Coriolis effect.
True or
False
Statement
A car traveling in a straight line at a constant speed of 50 mph has no
acceleration.
Acceleration measures the change in velocity of an object. Velocity is defined
by both speed and direction of motion as in "50 mph West". In this case both
the speed and direction of motion do not change.
1
TRUE
2
FALSE
A car makes a right turn while traveling at a constant speed of 20
mph. Since the car’s speed does not change during the turn, it has no
acceleration.
Acceleration measures the change in velocity of an object. Velocity is defined
by both speed and direction of motion. "20 mph West" and "20 mph North"
are two different velocities. The velocity of the car does change in this case
and so it has acceleration.
When no force is applied to an object, it moves in a straight line.
Force causes acceleration. When no forces are applied, objects move in a
straight line at constant speed.
3
TRUE
When a car stops quickly, you move forward because your body wants
to continue its steady motion.
Your body tends to keep moving at the original steady speed. Your seatbelt is
designed to apply a force rearward to decelerate your body.
4
TRUE
5
FALSE
When you turn left in a car, a force pulls you to the right.
There is no object or cause of a force that pulls you opposite to the turn. Your
body has mass that tends to continue in a straight line and not follow the turn.
Your seat will apply a force to accelerate your mass to the left to follow the
curve.
Objects standing still on a rotating Earth have an acceleration.
The objects move in a circle as the Earth completes a rotation once every 24
hours. Since they do not travel in a straight line, they have acceleration.
6
TRUE
Objects standing still on the Equator are rotating with the Earth at
over 1000 mph.
A person standing on the Equator must complete one rotation covering 25000
miles in 24 hours. This gives a speed over 1000 mph.
7
TRUE
100
Ocean Motion
Overall Score (%)
Teacher Guide
Lesson
2
3
Explore: A Model of Fluid Circulation
What drives the Trade Winds?
Heating a fluid like air or water from beneath can make a fluid unstable. A warmed fluid
becomes less dense and will rise opposite to the force of gravity. The cooler fluid above will
move to replace the rising warm fluid and it will be warmed itself. This cycle repeats to mix
the fluid. The process of convection describes motions in a fluid that result in the transport
and mixing of the fluid properties. Suppose you heat a container of water on a stove burner.
1. What sort of motion happens in the water?
As the liquid on the bottom becomes hot, there is a circulation of
water from the bottom of the pot to the top. This movement is
called convection. It mixes the water so its temperature becomes
more uniform.
2. Why does this kind of water motion occur?
The water on the bottom is heated directly by the stove burners
and so its temperature rises quickly compared to the cooler water
above. The heated water has a lower density than the water above
so the hot water moves up as the cooler water moves down.
3. Imagine now that you put the same pot of water into an oven with a top broiler (heat
source above the water surface). What kind of movement of the water would you expect in
this case? The top surface of the liquid is closest to the broiler and you would expect this
surface to heat fastest. The temperature of this surface water would increase, the surface
water’s density would decrease and it would remain at the surface. The cooler, denser water
below the surface would remain thermally isolated. In this case, heating causes more fluid
stability. The warm surface water will not tend to mix with cooler water below.
4. Suppose you were asked to make a prediction about how water temperature in the ocean
varies with the depth of the water. Which model – pot heated from the bottom or from the top
– applies to the ocean? As you go deeper in the ocean, will the water become cooler or
warmer? What effect will the temperature of the surface water have on the air above?
The ocean is heated from above by the sun, so the model of the pot heated from above is
correct. The surface water will not easily mix with the deeper cold water. Heat energy will
accumulate at the surface. One can expect that the ocean water will become cooler with
depth. Seawater is not transparent and so sunlight will not penetrate far beyond the surface.
The warm surface water will heat the air above.
5. To investigate further the origin of the trade winds, let’s consider the speed at which the
Earth rotates at different locations. Click to see an animation of the Rotating Earth during the
course of one day. Locate the following sites: a marked site on the Equator and London,
England. Which site travels the greatest distance during one revolution (24 hours)? Which site
has the greatest speed? Both sites travel in a circle. The site located on the Equator travels
the greater distance since the radius of its circle is larger. Both sites make one full revolution
(rotation) in 24 hours. The site that moves the greater distance in 24 hours has the higher
speed so the Equator site has the higher speed.
6. Imagine air moving southward from London to the Equator. As
it flows above the surface towards the Equator, it will pass over
surface that is moving faster and faster eastwards than the air.
The air will appear to fall behind the Earth’s rotation and curve to
the right as it moves. Here we define right and left as viewed by
someone facing the direction of motion of the air. Would the air
appear to move in a straight path on the rotating sphere?
The air would seem to curve westward, to the right from the
viewpoint of the air mass.
Ocean Motion
Teacher Guide
Lesson
2
4
7. Imagine the same air mass moving northward from the Equator. As it flows northward, it
will pass over surface that moves slower in an eastward direction. Will the air mass appear to
follow a straight line? Curve to the left? Or curve to the right?
The air would be moving faster eastward than the surface so it would curve eastward – curve
to the right as seen facing in the direction of motion of the air mass.
8. Imagine the same air mass moving southward from the Equator. As it flows southward, it
will pass over surface that moves slower in an eastward direction. Will the air mass appear to
follow a straight line? Curve to the left? Or curve to the right?
The air would be moving faster eastward than the surface so it would curve eastward – curve
to the left as seen facing in the direction of motion of the air mass.
George Hadley (1685-1768), an
English lawyer and amateur
meteorologist, first recognized the
reason the trade winds, a major wind
system blowing across the surface of
the Earth from 30o north and 30o south
latitudes toward the Equator,
preferentially blew westward. His
explanation depended on the fact that
the Earth is a rotating sphere and sites
on the surface of rotating sphere
travel with different speeds (travel
different distances in equal times).
The name, trade winds, derives from
the Old English ”trade”', meaning path
or track. The trade winds were a key
factor in ensuring that European
sailing vessels, including Columbus
reached North American shores.
Weather, which describes the current
state of the atmosphere, normally fluctuates daily due to a complex interplay of forces and
processes. Any steady or cyclic weather phenomena could be the result a dominating process.
These phenomena provide opportunities for scientific models and hypotheses to be tested.
Edmond Halley (1656-1742) correctly understood a role of the sun in atmospheric circulation.
He reasoned that intense solar radiation heated the air near the equator and caused it to
expand and rise up. This rising air was replaced by cooler air rushing in from higher (lower)
latitudes in the northern (southern) hemisphere. The circulation of the air would be driven by
a pressure-gradient force that would cause high-pressure (cooler, more dense) air to move
into regions of low pressure (warmer, less dense) air. This explanation predicted a flow of air
from the poles to the Equator where the air masses would converge but could not account for
the steady westward flow.
In 1686, when Edmond Halley, pictured on the left, proposed his
theory attempting to explain the trade winds, he was successful in
describing the overall circulation at the Equator. But he failed to
explain the westward component of the trades. Hadley earned fame
realizing that the Earth's rotation played a crucial role in the direction
taken by a moving airmass. George Hadley provided a description of
the equatorial trade winds that was essentially correct.
Ocean Motion
Teacher Guide
Lesson
2
5
Gaspard-Gustave de Coriolis (1792-1843), left a French mathematician,
mechanical engineer, and scientist, worked out the general formulas for
motion of objects measured from rotating systems of coordinates. He is
best known for his work on the Coriolis Effect. Coriolis was able to
determine the following simple rules for motions on the surface of a
rotating sphere:
• The apparent acceleration of objects on the rotating sphere is
perpendicular to their velocity.
• Objects traveling in the Northern Hemisphere curve to the right.
• Objects traveling in the Southern Hemisphere curve to the left.
When you twirl an object connected to a string around in a circle at steady speed, you are
experimenting with motion where the object’s velocity is perpendicular to its acceleration.
The string provides a force pulling toward the center (a centripetal force) that causes the
object to accelerate towards the center – to modify its velocity in the direction of the pull.
The Coriolis force is evident in swirling
vortex weather patterns (like
hurricanes), leading to a counterclockwise rotation in the Northern
Hemisphere and a clockwise rotation on
the Southern Hemisphere.
An example, right, is the beautifully
formed low-pressure system swirling off
the southwestern coast of Iceland.
Because this low-pressure system
occurred in the Northern Hemisphere,
the winds spun in toward the center of
the low-pressure system in a counterclockwise direction.
The Aqua MODIS instrument took the
image on September 4, 2003.
9. Suppose you twirl an object on a string around in a circle. What will be the effect of
increasing the speed of the object? Will it cause you to increase, decrease or keep the same
your pull on the string?
As the object rotates faster, the tension in the string will increase. If the object moves too
fast, the string tension required to keep the object moving in a circle will be too large and the
string will break.
10. Suppose you are challenged to twirl the object at a higher speed but must keep your pull
on the string the same. Would you increase, decrease or keep the same the length of the
string (the radius of the circle)?
As the string lengthens, the tension required becomes less. Basically, the object’s trajectory
has less curvature with a longer string. Its velocity changes less in direction during a time
interval, and this requires less force.
11. What happens if you release the string while the object is moving northward and you
have been pulling eastward? In what direction will the object move?
The object will continue moving northward.
Ocean Motion
Teacher Guide
Lesson
2
6
Uniform circular motion can be described as the motion of an object in a circle at a constant
speed. For circular motion to occur there must be constant force acting on a body pushing it
toward the center of the circular path. This force is the centripetal (center-seeking) force. As
an object moves in a circle, it is constantly changing direction. Because of this direction
change, you can be certain that an object undergoing circular motion is accelerating (even if it
is moving at constant speed).
The law for the centripetal acceleration (A) of object traveling at speed (V) in a circle of radius
(R) is:
A=
V2
R
Use this law to answer the following questions.
12. If the centripetal acceleration (A) is kept constant while the speed of the
object (V) is increased, what change must happen to the radius of curvature (R)
of the object’s trajectory? [increase, decrease, stay the same]
The radius must increase so the ratio remains the same.
13. If the object speed is kept the same and you observe that the radius of curvature of the
object’s trajectory is becoming smaller, what change is happening to the centripetal
acceleration? [increase, decrease, stay the same]
If the speed remains constant while the radius decreases, the ratio, V2/R, will increase in size
and so the centripetal acceleration will increase.
To help you better understand the Coriolis equation of acceleration on a rotating sphere, a
Coriolis Model has been made to simulate the motion of an object sliding without friction on a
sphere with the same size and rotational speed as the Earth. The object is allowed to slide
freely for 7 days and you are allowed to set the object’s starting velocity (speed and direction)
and position.
14. For your first four trials, use the Coriolis Model and complete the following four trials to
determine if the trajectory follows the two Coriolis Rules—illustrated below. For each trial
select the object’s speed and direction and the hemisphere indicated in the table.
Trial
1
2
3
4
Starting
Speed
(m/sec)
50
50
50
50
Trial 1
Ocean Motion
Starting
Direction
Starting
Hemisphere
North
North
East
West
North
South
North
South
Trial 2
Teacher Guide
Trial 3
Lesson
2
Trajectory
Follows
Rules
Yes
Yes
Yes
Yes
Direction
Trajectory
Curves
Right
Left
Right
Left
Trial 4
7
15. The Equator is the dividing line for the two rules to apply to moving objects. What might
happen if an object is launched in either hemisphere, but crosses over the equator during its
trajectory?
To test your understanding, make a prediction of what will happen to an object when it is
launched in the manner specified in each row of the following table. Check your predictions
using the Coriolis Accelerated Motion visualizer.
Trial Starting Starting
Speed
Direction
(m/sec)
Starting
Location
Predicted Trajectory
if object crosses Equator
5
50
South
15o North
6
50
North
15 o
South
7
50
East
15 o North
8
50
West
15 o
South
The object is launched
towards the Equator. Above
the Equator it should curve
to the right. After it crosses
the Equator it will curve left.
The object is launched
towards the Equator. Below
the Equator it should curve
to the left. After it crosses
the Equator it will curve
right.
The object is launched
eastward near the equator.
Above the Equator it should
curve to the right. After it
crosses the Equator it
should curve left.
The object is launched near
the Equator. Below the
Equator it should curve to
the left. After it crosses the
Equator it should curve
right.
Trial 5
Trial 6
Trial 7
Does your
prediction agree
or disagree with
visualizer?
Agrees
Agrees
Agrees
Agrees
Trial 8
As discussed previously in this lesson, the trade winds are driven by heated, light air at the
Equator rising up and drawing in cooler surface air slightly north and south of the Equator.
Ocean Motion
Teacher Guide
Lesson
2
8
It should be clear from the trajectories in trial 5 and trial 6 that
air rushing towards the Equator will curve towards the west no
matter if the air comes from the north or south. This creates a
pattern of easterly winds (winds blowing from the east) at the
Equator. Note that the air masses from the north and south will
collide at the Equator and that interaction will strengthen the
equatorial wind pattern. The computer model you have been
using models a sliding object freely moving over a smooth
Earth-sized sphere with nothing blocking its path as it slides
above or below the Equator. This is not the case for the air in
the atmosphere. The air rushing to the Equator will be driven
further in the westward direction by the converging air masses
and will not significantly cross the Equator.
16. Next, use the Coriolis Model to do a systematic study of
how the Coriolis acceleration varies with latitude. Henry Stommel referred to this variation as
the “beta effect.” Fill in the following tables and draw a conclusion about how the Coriolis
acceleration varies with latitude. You will need to use the centripetal acceleration law:
A=
V2
R
To indicate your estimates of radius and acceleration use the subjective relative scale: small,
medium, or large.
Note: The speed of the object is kept constant. In this case, the radius and acceleration are
inversely proportional (large R gives a small A; small R gives a large A):
Starting
Position
Starting
Speed
(m/sec)
Starting
Direction
85
45
15
15
45
85
50
50
50
50
50
50
East
East
East
East
East
East
N
N
N
S
S
S
Radius of Curvature
of Trajectory
(small, medium,
large)
Small
Medium
Large
Large
Medium
Small
Coriolis Acceleration
(small, medium, large)
Large
Medium
Small
Small
Medium
Large
17. What do you conclude about the effect of latitude on the Coriolis acceleration?
The Coriolis acceleration increases at higher latitudes.
Elaboration: Coriolis Acceleration and the Gulf Stream
How does latitude impact the Gulf Stream?
Look in lesson 3, for a study of an ocean basin model, which invites you to discover that the
existence of a very strong, narrow western boundary currents like the Gulf Stream are
dependent on the change of the Coriolis acceleration with latitude. Without this variation as
one moves towards the poles, western boundary currents would be less intense and boundary
currents along the east and west coasts of ocean basins would be similar.
Ocean Motion
Teacher Guide
Lesson
2
9
Evaluation: Matrix for Grading Lesson 2
4
Expert
3
Proficient
2
Emergent
1
Novice
Ocean Motion
Responses show an in-depth understanding of models and explorations used
to explain scientific concepts and processes used in the lesson. Proficient
manipulation of computer models. Data collection and analysis of data are
complete and accurate. Predictions and follow through with accuracy of
predictions are explained and fully supported with relevant data and
examples.
Responses show a solid understanding of models and explorations used to
explain scientific concepts and processes used in the lesson. Mostly proficient
manipulation of computer models. Data collection and analysis of data are
mostly complete and accurate. Predictions and follow through with accuracy
of predictions are explained and mostly supported with relevant data and
examples.
Responses show a partial understanding of models and explorations used to
explain scientific concepts and processes used in the lesson. Some
proficiency in manipulation of computer models. Data collection and analysis
of data are partially complete and sometimes accurate. Predictions and follow
through with accuracy of predictions are sometimes explained and supported
with relevant data and examples.
Responses show a very limited understanding of models used to explain
scientific concepts and processes used in the lesson. Little or no ability shown
to manipulate computer models. Data collection and analysis of data are
partially complete and sometimes accurate. Predictions and follow through
with accuracy of predictions are not well explained and are not supported
with relevant data and examples.
Teacher Guide
Lesson
2
10