Download Ok, so what I did the first step was just flip the diagram over on its

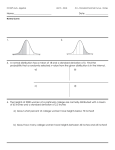
Each segment makes up 35.35% of the population
to equal 68.3%
65.0
62.2
71.1
56.1
63.6
99% of the data falls
within these points
Ok, so what I did the first step was just flip the diagram over on its side so that it is easier
to see.
Women’s Height. The accompanying box plot depicts heights (in inches) of a large
collection of randomly selected adult women. What does it kind of resemble now? It
kind of looks like a normal distribution! The numbers corresponding to 62.2 and 65.0
represent heights which fall within ± 1 standard deviation from the mean – which means
that 68.3% of the population will fall within these two values. However, we can also expect
that 95% of the population falls within 95% of two standard deviations from the mean.
The numbers at the end represent the two extremes – they are called the lower inner
fences – and we expect that 99% of the data falls within these numbers as they are
approximately 3 standard deviations from the mean.
A). what is the mean height of the adult women? – the mean height is the number
which is in the middle of the box – 63.6
B). If one of these women is randomly selected, find the probability that her height is
between 56.1 in. and 62.2 inches. Ok here this spans from the 3rd standard deviation
to the 1st standard deviation. This would be (99/2)-35.35 = 14.15%
C). If one of these women is randomly selected, find the probability that her height is
below 62.2 in. and above 63.6 in. – this is basically asking for 1 standard deviation
from the mean which is 35.35%
D). If two women are randomly selected, find the probability that they both have heights
between 62.2 in. and 63.6 in. If one women was selected, her probability would be
35.35% that she was in-between these 2 values. However, I will firstly assume that
the 2 people are independent.
Given the formula
= then it would be (35.35%)(35.35%)=
12.5%
E) If five women are randomly selected, find the probability that three of them are taller
then the mean and the other two are shorter than the mean.
Here – three are taller then the mean and two are shorter then the mean – this is a
trick question! As you read above, this box plot is symmetrical, and the probability
of being above or below the means are equal (which is true since the problem states
that we have a large sample size)