Download Determine Whether an Ordered Pair is a Solution

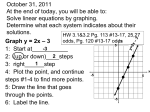
Math 102
6.1A "Systems of Two Linear Equations in Two Variables"
Objectives:
* Determine whether an ordered pair is a solution of a system.
* Solve systems of linear equations by graphing.
* Use graphing to identify inconsistent systems.
Determine Whether an Ordered Pair is a Solution of a System
De…nition:
"Solution of a System"
kA solution of a system of equations in two variables is an ordered pair that satis…es both equations of the system.k
Example 1: (Determining whether an ordered pair is a solution)
Determine whether (6; 2) is a solution of the system of equations:
(
x
2y = 10
y = 3x
20
Solve Systems of Linear Equations by Graphing
To solve a system of equations means to …nd all the solutions of the system. One way to solve a system of linear equations
in two variables is to graph each equation and …nd where the graphs intersect.
The Graphing Method:
Step 1 : Graph each equation on the same plane
Step 2 : Find the intersection points (the coordinates of these points are solutions to the system)
Step 3 : If the graphs have no point in common, the system has no solution
Step 4 : Check your solution by plugging the values into the system
De…nition:
"Consistent System"
is called a consistent system.
A system of equations with
De…nition:
"Inconsistent System"
A system of equations with
is called an inconsistent system.
Page: 1
Notes by Bibiana Lopez
College Algebra by Kaufmann and Schwitters
6.1
Example 2: (Consistent systems)
Solve8the following systems of equations by graphing.
< x 3y = 5
a)
: 2x + y = 4
y
8
< 5x + 2y = 6
b)
: 10x 4y =
12
8
y
6
4
4
2
2
-8 -6 -4 -2
-2
2
4
6
8
x
-4
-4
-2
2
4
-2
x
-6
-4
-8
Example 4: ( Inconsistent system)
8
< 3y
: 2x
Solve the system of equations by graphing (if possible):
y
2x = 6
3y = 6
4
2
-4
-2
2
4
x
-2
-4
In summary we have:
y
4
y = 2x + 3 2
-4
-2
y
2
y
2y = -x + 4
4
x
-4
4
y = 3x + 2
2y = 4x + 6
2
-2
4
-4
-2
y=x+2
2
-2
4
x
-4
2
-2
2
-4
-4
4
-2
x
y = 3x - 1
If the lines coincide, the system
If the lines are di¤erent and intersect,
If the lines are di¤erent and parallel,
is consistent and dependent.
the system is consistent.
the system is inconsistent.
(In…nitely many solutions)
(One solution)
Page: 2
(No solution)
Notes by Bibiana Lopez