Download PH_Geo_2-2_Biconditionals_and_Definitions[1]

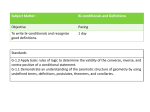
Sec. 2-2
Biconditionals & Definitions
Objectives:
a) To write biconditionals
b) To recognize good
definitions
I. Biconditionals
Connect the conditional (if – then) and its
converse
Only when both are true
Use “if and only if” (iff)
II. Writing iffs
1.
Look at conditional and decide if true.
2.
Write the converse and decide if true.
3.
Combine statements with “if and only if”
Example 1: Writing an iff
Conditional: If 2 angles have the same
measurement, then the angles are
congruent.
Converse:
If two angles are congruent, then they have
the same measurement.
Iff:
Two angles have the same measurement iff
the angles are congruent.
Example 3A: Analyzing the Truth Value of a
Biconditional Statement
Determine if the biconditional is true. If false,
give a counterexample.
A rectangle has side lengths of 12 cm and 25 cm
if and only if its area is 300 cm2.
Example 3A: Analyzing the Truth Value of a
Biconditional Statement
Conditional: If a rectangle has side
lengths of 12 cm and 25 cm, then
its area is 300 cm2.
The conditional
is true.
Converse: If a rectangle’s area is
300 cm2, then it has side lengths
of 12 cm and 25 cm.
The converse
is false.
If a rectangle’s area is 300 cm2, it could have
side lengths of 10 cm and 30 cm. Because the
converse is false, the biconditional is false.
p
q means p
q and q
p
Writing Math
The biconditional “p if and only if q” can also be
written as “p iff q” or p  q.
III. Good Definitions
In geometry we started with undefined terms
(point, line, & plane) whose meaning we
took w/o proof.
Next we used, these undefined terms to
define our next set of terms. Such as
collinear and midpoint.
All good definitions must be biconditionals.
Helpful Hint
Think of definitions as being reversible.
Postulates, however are not necessarily true
when reversed.
Example 2: Writing a good definition
Statement: A midpoint divides a segment into
two congruent parts.
Conditional:
If a point is a midpoint, then it divides a
segment into two congruent parts. (T or F)
Converse:
If a point divides a segment into two congruent
parts, then it is a midpoint. (T or F)
Iff:
A point is a midpoint, iff it divides a segment
into two congruent parts.
Example 3: Writing an iff
Statement: A right angle has a measure of 90°.
Conditional:
If an angle is a right angle, then it has a measure
of 90°. (T or F)
Converse:
If an angle has a measure of 90°, then it is a right
angle. (T or F)
Iff:
An angle is a right angle, iff it has a measure of
90°.
What have I learned Today?
What is another word for biconditionals?
Iff (if and only if)
How do you form iffs?
Combine both the conditional and the converse.
Do they both have to be true?
Heck yeah!