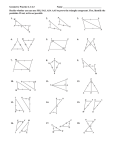
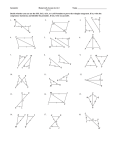
* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Prove Triangles Congruent with SSSSAS<ASA
Reuleaux triangle wikipedia , lookup
Technical drawing wikipedia , lookup
Multilateration wikipedia , lookup
Rational trigonometry wikipedia , lookup
Trigonometric functions wikipedia , lookup
Euler angles wikipedia , lookup
History of trigonometry wikipedia , lookup
Pythagorean theorem wikipedia , lookup
G.6 Proving Triangles Congruent 1 Visit www.worldofteaching.com For 100’s of free powerpoints. 2 The Idea of Congruence Two geometric figures with exactly the same size and shape. F B A C E D 3 How much do you need to know. . . . . . about two triangles to prove that they are congruent? 4 Corresponding Parts Previously we learned that if all six pairs of corresponding parts (sides and angles) are congruent, then the triangles are congruent. 1. AB DE 2. BC EF 3. AC DF 4. A D 5. B E 6. C F ABC DEF 5 Do you need all six ? NO ! SSS SAS ASA AAS HL 6 Side-Side-Side (SSS) If the sides of one triangle are congruent to the sides of a second triangle, then the triangles are congruent. Side Side 1. AB DE 2. BC EF 3. AC DF Side ABC DEF The triangles are congruent by SSS. 7 Included Angle The angle between two sides HGI G GIH I GHI H This combo is called side-angle-side, or just SAS. 8 Included Angle Name the included angle: E Y S YE and ES YES or E ES and YS YSE or S YS and YE EYS or Y The other two angles are the NON-INCLUDED angles. 9 Side-Angle-Side (SAS) If two sides and the included angle of one triangle are congruent to the two sides and the included angle of another triangle, then the triangles are congruent. included angle Side Side 1. AB DE 2. A D 3. AC DF Angle ABC DEF The triangles are congruent by SAS. 10 Included Side The side between two angles GI HI GH This combo is called angle-side-angle, or just ASA. 11 Included Side Name the included side: E Y S Y and E YE E and S ES S and Y SY The other two sides are the NON-INCLUDED sides. Angle-Side-Angle (ASA) 12 If two angles and the included side of one triangle are congruent to the two angles and the included side of another triangle, then the triangles are congruent. included side 1. A D 2. AB DE 3. B E Angle Side Angle ABC DEF The triangles are congruent by ASA. Angle-Angle-Side (AAS) 13 If two angles and a non-included side of one triangle are congruent to the corresponding angles and side of another triangle, then the triangles are congruent. Non-included side 1. A D 2. B E 3. BC EF Angle Side Angle ABC DEF The triangles are congruent by AAS. 14 Warning: No SSA Postulate There is no such thing as an SSA postulate! Side Angle Side The triangles are NOTcongruent! 15 Warning: No SSA Postulate There is no such thing as an SSA postulate! NOT CONGRUENT! BUT: SSA DOES work in one situation! 16 If we know that the two triangles are right triangles! Side Side Side Angle 17 We call this HL, for “Hypotenuse – Leg” Hypotenuse Hypotenuse Leg RIGHT Triangles! These triangles ARE CONGRUENT by HL! Remember! The triangles must be RIGHT! Hypotenuse-Leg (HL) 18 If the hypotenuse and a leg of a right triangle are congruent to the hypotenuse and a leg of another right triangle, then the triangles are congruent. Right Triangle Leg 1.AB HL 2.CB GL 3.C and G are rt. ‘s ABC DEF The triangles are congruent by HL. 19 Warning: No AAA Postulate There is no such thing as an AAA postulate! Same Shapes! E B A C D NOT CONGRUENT! Different Sizes! F Congruence Postulates and Theorems 20 • SSS • SAS • ASA • AAS • AAA? • SSA? • HL 21 Name That Postulate (when possible) SAS SSA Not enough info! ASA AAS 22 Name That Postulate (when possible) AAA SSA Not enough info! Not enough info! SSS SSA HL 23 Name That Postulate (when possible) Not enough info! Not enough info! SSA SSA HL Not enough info! AAA Vertical Angles, Reflexive Sides and Angles 24 When two triangles touch, there may be additional congruent parts. Vertical Angles Reflexive Side side shared by two triangles 25 Name That Postulate (when possible) Reflexive Property SAS Vertical Angles AAS Vertical Angles SAS Reflexive Property SSA Not enough info! 26 Reflexive Sides and Angles When two triangles overlap, there may be additional congruent parts. Reflexive Side side shared by two triangles Reflexive Angle angle shared by two triangles Let’s Practice 27 Indicate the additional information needed to enable us to apply the specified congruence postulate. For ASA: B D For SAS: AC FE For AAS: A F 28 What’s Next Try Some Proofs End Slide Show Choose a Problem. Problem #1 SSS Problem #2 SAS 29 End Slide Show B A C D A C B E D X Problem #3 ASA W Y Z Problem #4 Given: A C BE BD Prove: ABE CBD AAS A C B E Statements D Reasons Given Vertical Angles Thm Given 4. ABE CBD AAS Postulate 55 Problem #5 HL A Given ABC, ADC right s, AB AD Prove: 3. AC AC ABC ADC B Statements 1. ABC, ADC right s AB AD D C Reasons Given Given Reflexive Property 4. ABC ADC HL Postulate 57 58 Congruence Proofs 1. Mark the Given. 2. Mark … Reflexive Sides or Angles / Vertical Angles Also: mark info implied by given info. 3. Choose a Method. (SSS , SAS, ASA) 4. List the Parts … in the order of the method. 5. Fill in the Reasons … why you marked the parts. 6. Is there more? 59 Given implies Congruent Parts midpoint parallel segment bisector segments angles segments angle bisector angles perpendicular angles 60 Example Problem Given: AC bisects BAD AB AD Prove: ABC ADC A B C D 61 … and what it implies Step 1: Mark the Given Given: AC bisects BAD AB AD Prove: ABC ADC A B C D 62 Step 2: Mark . . . Given: AC bisects BAD AB AD Prove: ABC ADC •Reflexive Sides •Vertical Angles A B C D … if they exist. 63 Step 3: Choose a Method Given: AC bisects BAD AB AD Prove: ABC ADC SSS SAS ASA AAS HL B A C D 64 Step 4: List the Parts Given: AC bisects BAD AB AD Prove: ABC ADC STATEMENTS S AB AD A S BAC DAC A B C D REASONS AC AC … in the order of the Method 65 Step 5: Fill in the Reasons Given: AC bisects BAD AB AD Prove: ABC ADC STATEMENTS B A C REASONS S AB AD Given A S BAC DAC Def. of Bisector Reflexive (prop.) AC AC D (Why did you mark those parts?) 66 Step 6: Is there more? Given: AC bisects BAD AB AD Prove: ABC ADC STATEMENTS S 1. AB AD 1. 2. AC bisects BAD 2. A 3. BAC DAC 3. 4. S 4. AC AC 5. ABC ADC 5. A B C REASONS Given Given Def. of Bisector Reflexive (prop.) SAS (pos.) D 72 Congruent Triangles Proofs 1. Mark the Given and what it implies. 2. Mark … Reflexive Sides / Vertical Angles 3. Choose a Method. (SSS , SAS, ASA) 4. List the Parts … in the order of the method. 5. Fill in the Reasons … why you marked the parts. 6. Is there more? 73 Using CPCTC in Proofs According to the definition of congruence, if two triangles are congruent, their corresponding parts (sides and angles) are also congruent. This means that two sides or angles that are not marked as congruent can be proven to be congruent if they are part of two congruent triangles. This reasoning, when used to prove congruence, is abbreviated CPCTC, which stands for Corresponding Parts of Congruent Triangles are Congruent. 74 Corresponding Parts of Congruent Triangles For example, can you prove that sides AD and BC are congruent in the figure at right? The sides will be congruent if triangle ADM is congruent to triangle BCM. Angles A and B are congruent because they are marked. Sides MA and MB are congruent because they are marked. Angles 1 and 2 are congruent because they are vertical angles. So triangle ADM is congruent to triangle BCM by ASA. This means sides AD and BC are congruent by CPCTC. Corresponding Parts of Congruent Triangles 75 A two column proof that sides AD and BC are congruent in the figure at right is shown below: Statement Reason MA MB Given A B Given 1 2 Vertical angles ADM BCM ASA AD BC CPCTC Corresponding Parts of Congruent Triangles 76 A two column proof that sides AD and BC are congruent in the figure at right is shown below: Statement Reason MA MB Given A B Given 1 2 Vertical angles ADM BCM ASA AD BC CPCTC Corresponding Parts of Congruent Triangles 77 Sometimes it is necessary to add an auxiliary line in order to complete a proof For example, to prove ÐR @ ÐO in this picture Statement Reason FR @ FO Given RU @ OU Given UF @ UF reflexive prop. DFRU @ DFOU SSS ÐR @ ÐO CPCTC Corresponding Parts of Congruent Triangles 78 Sometimes it is necessary to add an auxiliary line in order to complete a proof For example, to prove ÐR @ ÐO in this picture Statement Reason FR @ FO Given RU @ OU Given UF @ UF Same segment DFRU @ DFOU SSS ÐR @ ÐO CPCTC