Download pptx

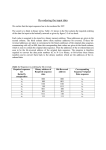
Lecture 19 Outline:
Block-by Block Convolution, FFT/IFFT,
Digital Spectral Analysis

Announcements:
Reading: “5: The Discrete Fourier Transform” pp. 13-15, 18, 19+block
diagram at top of pg 20, pp. 27.
 HW 6 due today with free extension to Thurs. 5pm
 Graded midterms ready for pickup (with TAs after class or from Julia)


Example of Linear Convolution from Circular

Block-by-block convolution: Overlap/Add

FFT/IFFT and its Complexity

Digital Spectral Analysis
Midterm Postmortem


Graded midterms/solns available (from TAs/Julia)
Grading Histogram
??

Regrade requests must be submitted in writing


Median: 65.25
Mean: 67.77
Std. Dev: 24.46
Low: 24
High: 98
Describe grading error that occurred; partial credit fixed
Course grade from all coursework: B+ class average

Before extra credit; extra credit points added to HW grade
Review of Last Lecture

Computing circular convolution:
 Linearly convolve ~
x1 n  and ~
x2 n 



x1 n  N
 N 1 ~
 x1 m  ~
x2 n  m  0  n  N  1
x2 n   m
0

0
otherwise

Place sequences on circle in opposite directions, sum up all pairs,
rotate outer sequence clockwise each time increment
Linear Convolution using Circular Convolution
0  n  L 1
 xn 
x n   
 Zero pad x[n] by appending P-1 zeros:
 0 L  n  L P2
0  n  P 1
hn
 Zero pad h[n] by appending L-1 zeros:
h n  
 0 PnL P2
 Both sequences are of length M=L+P-1, same as y[n]
 Take circular convolution of zero padded sequences

 This yields the linear convolution:
 x n  h n  0  n  M  1
yn   xn * hn  
zp
zp



zp

M
0
zp
otherwise
Example: Linear from Circular

Linear Convolution
x1 n 
1
0 1 2
3
L=4
n
4

3 4 5
4
3
2
2
1
1
P=6
n
x1 n  6 x2 n  |n  4
x1[n] * x2[n]
4
3
x2 [ n ]
0 1 2
4
1
0
1
2
3 4
5
6
n
7
n
8
0 1 2
4
3
5
Linear from Circular with Zero Padding
1
x1, zp n 
1
0 1 2
3 4 5
x1, zp n  9 x2, zp n 
0
1
M=L+P-1=9
1
1
0
6 7 8
n
1
1
0
1
1
0
0
1
0
1
1
1
0
1
1
0
1
x2, zp [n ]
1
0
0 1 2
3 4 5 6 7 8
n
1
0
0
0
1
1
1
n=0
0
0
1
0
n=1
0
Block Convolution using
Overlap Methods

Want block-by-block linear convolution for long sequences


Uses fixed hardware. Has fixed delay/complexity
Goal: compute linear convolution of x[n] and y[n]
x[n] very long, h[n] has length P
 Want to break x[n] into shorter blocks and compute portions of
y[n] block-by-block.


P 1
m 0
m 0
yn   xn * hn    xm hn  m    xn  m hm 

Overlap-Add Method


Breaks x[n] into non-overlapping segments of length L: xn   x r n
r 0
 xn rL  n  r  1L  1
x r n  
 0


otherwise

Convolve each segment with h[n] and sum: yn  xn * hn   x r n * hn
r 0
These convolutions computed using DFT:

xr n * hn  xr ,zp n  N hzp n   FFT 1 FFT xr ,zp n  FFT hzp n 
Overlap-Save
(Not responsible for this topic; pp. 15-16)

Breaks x[n] into segments of length L>P, each segment
overlapping with previous one at P-1 points

Perform L-point circular convolution of each segment
with zero-padded filter h[n] (using DFT): y n  x n h n
r ,p

r

L
zp
Identify portion of each circular convolution that
corresponds to a linear convolution, and save it.

First P – 1 points are unusable, while the remaining L – P + 1
points correspond to a linear convolution.

Thus, we save L – P + 1 points from each circular convolution.

Because first P – 1 points are unusable, the input segments must
overlap at P – 1 points. yn   y n  r L  P  1  P  1
 y n P  1  n  L  1
y r n   r ,p
otherwise
 0

r 0
r
Blocklength Choice

In overlap methods, several factors affect the
choice of the block length L



a shorter block length minimizes latency.
a shorter block length minimizes memory required for
performing the FFTs, multiplication, and inverse FFT.
Given P (length of h[n]), there is an optimal block
length L that minimizes complexity.



L too short, complexity increased by overhead of
adjacent block overlap
L too long, complexity increased because FFT
complexity increases with the block length
In practice, set block length so that FFT blocklength is
an integer power of 2 (required for FFTs)
FFT and IFFT Algorithms

FFT computes the DFT of a sequence, IFFT
  
computes the inverse DFT:     
xn 




1
N
N 1
X k WNkn
k 0
X k 
N 1
x n W Nkn
n 0
DFT as matrix operation: N2 complex multiplies (lect. 16)
Complexity of FFT and IFFT same: DFT X k   N1 DFTX k 
1
*
*
FFT/IFFT breaks down a DFT with N2 complex
multiplies into many smaller DFTs with N multiplies
Reduces complexity of computing N-point DFT or
IDFT from N2 complex multiplies to .5Nlog2N
N
2
N2
N
log 2 N
2
N
N2
16
256
32
8.0
128
16,384
448
36.6
1,024
1,048,576
5,120
204.8
8,192 67,108,864
53,248
1260.3
log 2 N
- In 1994 Strang described the FFT as "the most
important numerical algorithm of our lifetime”
- Included in Top 10 Algorithms of 20th Century
by IEEE Journal of Computing in Science and
Engineering
Digital Spectral Analysis
(ppt slide only)
Original CT Signal
s c t   Sc  j
...
Anti-Aliasing
Lowpass Filter
H aa  j
Filtered CT Signal
xc t   X c  j
A
Sampled, Windowed Signal
vn  xn wn
D
Sampled Signal
xn  xt  t nT ,    n  
t  nT
Zero-Pad
To Length
N≥L
B
vn  0  n  L  1

 0 L  n  N 1
E
Form Block
of Length
L
N-Point
DFT
Block of L Signal Samples
xn, 0  n  L  1
...
C
Block of N Spectral Samples
V k , 0  k  N  1
F
Window of Length L
wn, 0  n  L  1

Analog spectrum analysis:
 Analog signal input to a narrow BPF with tunable center frequency.
 The center frequency is swept over some range
 Signal recorded (amplitude and phase) to obtain CTFT estimate
 Can be used at any frequency range: audio, radio and microwave, optical, …

Digital spectrum analysis is as shown in the block diagram
 Sampler (ADC) technology limited to ~100 GHz; signals with BW>50 GHz distorted
 Windowing reduces distortion of FIR approximation to IIR signal
 Digital spectrum analysis is cheaper, smaller, and consumes less power than analog
 Used by all small electronic devices that must do spectrum analysis (e.g. WiFi)
Main Points

For linear convolution of long sequences, computation is
done in L-length blocks using overlap-add or overlap-save



The FFT and IFFT drastically reduce the complexity of
the DFT/IDFT computation


Methods are very similar, differ in where overlap is introduced
Choice of L optimizes tradeoff in latency, memory, and complexity
These algorithms are responsible for the widespread use of digital
signal processing in today’s electronic devices
Using low-complexity FFTs and IFFTs, spectral analysis
can be done with low-cost, low-power, small devices