Download Unit 6 ~ Contents

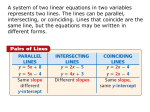
Unit 6 ~ Contents
6.1
6.2
6.3
6.4
6.5
6.6
6.7
6.8
6.9
6.10
6.11
6.12
6.13
6.14
6.15
6.16
Algebra Beauty and Awe ~ Music. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1
Systems of Equations . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
Graphing From the x- and y-Intercepts . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
Factoring Perfect Square Trinomials . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9
Solving Systems of Equations by Substitution . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12
Quiz 1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17
What Does it Look Like When Stars Sing? . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17
Box-and-Whisker Plots . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18
Factoring Trinomials in the Form x 2 + bx + c . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22
Simplifying a Radical With Numerical and Variable Factors . . . . . . . . . . . . . . . . . . . 27
Rational Expressions: Excluded Values . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 30
Quiz 2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 34
Turn Off That Noise! . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 34
Rational Expressions: Canceling Factors . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 36
Solving Systems of Equations by Addition/Elimination. . . . . . . . . . . . . . . . . . . . . . . 39
Reviewing Uses of the Negative Sign . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 42
Equalities Between Identical Formulas . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 46
Review for Test . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 52
Test . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 54
ΦHarmony All AroundΦ. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 54
6.1
Systems of Equations
If two linear equations are graphed on the same coordinate plane, they form a system of
equations. There are three possible results.
y
y = –3x – 2
1. Equations equivalent to each other will graph on top of each
other (Example: y = –3x – 2 and 2y = – 6x – 4). Every
solution for one equation is also a solution for the other.
2y = – 6x – 4
x
Such systems of equations are described as dependent.
dependent:
all solutions common
y
2. Equations which are not equivalent but have the same
slope will graph as parallel lines (Example: y = 2x + 1
and y = 2x – 3). These equations have no solutions in
common.
y = 2x + 1
x
y = 2x – 3
Such systems of equations are described as inconsistent.
inconsistent:
no solutions in common
y
3. Equations having different slopes will intersect at one
point (Example: y = x + 3 and y = – 2x). These
equations have exactly one solution in common—the
point of intersection.
Such systems of equations are described as consistent.
(–1, 2)
y=x+3
y = – 2x
consistent:
one solution in common
2 ~ Algebra I Unit 6
x
Label the systems as dependent, inconsistent, or consistent. 6.1
1.
y
2.
y
x
3.
y
x
x
Review
Factor the binomials when possible. 5.14
4. (9x 2 – 25)
5. (r 2 – s 2)
6. (x 2 – 144)
Use the five steps to set up and solve the equations. 5.13
7. At the end of one business day Cynthia had $753 of currency in her cash register consisting of twice
as many $20 bills as $10 bills, five times as many ones plus three as tens, and six more fives than
tens. How many of each were there?
8. Matthew purchased 360 board feet of rough-sawn lumber consisting of white oak at $1.65 per board
foot and red oak at $1.85 per board foot. How many board feet of each did he purchase if the total
cost was $621?
9. Before getting on the highway for a trip Charles filled up the 20-gallon tank in his car. He then began
driving at 60 mph. After 10 minutes a stone punctured his gas tank which began leaking at 0.25 gallons per minute. If his car averages 20 mpg, how long will it be until his car sputters to a stop from
having no fuel? (Note: 20 mpg = 0.05 gal/min.)
10. A 450-gallon stock tank has two drains, one of which lets water out 1 gallon per minute faster than the
other. With both drains open the tank will drain in 50 minutes. How fast does each drain let out water?
Multiply the polynomials. 4.12
11. (– 3x – 1)(3x 2 – x – 5)
12. (2x 2 – 3xy + y 2)(– 3x – y)
Simplify the radicals if possible. 5.3
13. √72
Solve the inequalities. 5.7
16. 7x < 20 – 3x
14. √75
15. √128
17. 2x – 14 ≥ 3 – 15x
18. – 5x – 18 < 2
6.1 Systems of Equations ~ 3
Draw the solution graph for each equation, using the given values for x. 4.9
19. x – 4y = –10 x = – 2, 2, 6
20. 7x + 2y = 35 x = 3, 5, 7
Simplify the binomials mentally (square-double-square). 4.14
21. (2x + 5)2
22. (3m – n)2
Subtract the polynomials. 3.11
24. (3x 2 – 2x + 2) – (5x 2 + 1)
23. (1 – 6x)2
25. (4x – 2y + 4) – (–10x – 3y + 9)
Factor the GCF out of the polynomials. 3.12
26. 9x 2y – xy + 2xy 2
27. 6x 2yz + 3x 2y
Use the five steps to set up and solve the equations. 5.11
28. Cindy has twice as many nickels as dimes and three fewer quarters than dimes. How many of each
does she have if their total worth is $6?
29. Tom Long chartered a bus to take a group of families to the National Aquarium. Adults paid $24.75
and children paid $18.75 for a total of $989.25 for the bus costs. With a total of 47 passengers, how
many adults and children were on the bus?
Graph the equations, using slope-intercept form. 5.12
1
6
30. x – 7y = 7
31. y = – x + 3
32. y = – x – 6
5
5
Label the systems as dependent, inconsistent, or consistent. 6.1
34.
y
35.
x
4 ~ Algebra I Unit 6
y
x
33. 7x – 3y = 15
36.
y
x
6.2
Graphing From the x- and y-Intercepts
y
The point on a graph where a line crosses the x-axis is called
the x-intercept. For all x-intercepts the y-value is 0. The point
where the line crosses the y-axis is called the y-intercept. For all
y-intercepts the x-value is 0.
(0, 2)
Suppose a line crosses the x-axis at 5; the y-value of that point is
0. Similarly, if the line crosses the y-axis at 2, the x-value of the
ordered pair is 0.
(5, 0)
x
This characteristic of x- and y- intercepts can be used to graph an equation. First find the
y-intercept by substituting 0 for x and solving the equation. Then find the x-intercept by substituting
0 for y and solving the equation again. This method of graphing can be done even when an
equation is not in slope-intercept form.
Example 1. Graph the equation 3x + 2y = 6 by finding the x- and y- intercepts.
3x + 2y = 6
3(0) + 2y = 6
y=3
3x + 2y = 6
3x + 2(0) = 6
x=2
Original equation.
x set equal to 0.
(0, 3)
Equation solved for y.
The y-intercept = (0, 3).
y
(2, 0)
x
Original equation.
y set equal to 0.
Equation solved for x.
The x-intercept = (2, 0).
6.2 Graphing From the x- and y-Intercepts ~ 5
Example 2. Graph the equation 3x – 4y = 6 by finding the x- and y-intercepts.
3x – 4y = 6
3(0) – 4y = 6
3
y=–
2
3x – 4y = 6
3x – 4(0) = 6
x=2
Original equation.
x set equal to 0.
y
Equation solved for y.
3
The y-intercept = (0, – ).
2
Original equation.
(0, – 3 )
2
(2, 0)
x
y set equal to 0.
Equation solved for x.
The x-intercept = (2, 0).
The y-intercept is 0 for all equations in standard form that have 0 for C. To graph a standard form
equation such as Ax + By = 0, transform the equation to slope-intercept form. Then use (0, 0) as
the y-intercept and the slope to establish a second point to graph the line.
Example 3. Graph the equation 3x – 2y = 0.
The graph for this equation passes through the origin (0, 0).
The slope is needed to graph the solution, so transform the
equation to slope-intercept form.
3x – 2y = 0
y=
3
x
2
y
Original equation.
Slope-intercept form.
The slope is
x
3
.
2
Time-Saver Tip
When an equation in standard form Ax + By = C is solved for y, it is changed to slope-intercept
C
C
A
A
form; y = – x + . Notice that the slope is – and the y-intercept is
This shows that the slope of
B
B
B
B
an equation in standard form is the opposite of the value of A over the value of B. It also shows that
the y-intercept is the value of C divided by the value of B. For example, the slope of the line for the
3
3
6
equation 3x – 2y = 6 is –(
) = . The y-intercept is
= 3.
–2
2
2
6 ~ Algebra I Unit 6
Graph each of the equations using the x- and y-intercepts or origin and slope. 6.2
1. x – 2y = 6
3. 2x – 3y = 0
2. – x + y = 7
4. 9x + 4y = –18
Review
Label the systems as dependent, inconsistent, or consistent. 6.1
5.
y
y
6.
x
Simplify the radicals. 5.9
8. √r 6
x
3
9. √x 7
12. (3, 1)(5, 5)
Multiply the sum and difference binomials mentally. 5.8
14. (2x 3 + 1)(2x 3 – 1)
x
10. √x 3y
Determine the slope of the lines passing through these points. 5.4
11. (–3, 2) (3, – 2)
y
7.
15. (2 – y 2)(2 + y 2)
Solve the equations by eliminating the fractions. 3.9
x
14 x
x
3
x
17.
=
–
18.
–
=1+
2
3
6
6
2
3
13. (– 4, –3)(–1, – 5)
16. (rs – 4)(rs + 4)
19.
8x
–x=5
3
Use the five steps to set up and solve the equations. 5.13
20. To make repairs to a 750-gallon fish tank at the local zoo, workers first opened the drain which lets
water out at 7 gallons per minute. 10 minutes later they added a 5-gallon-per-minute pump and 4
minutes after that they found and added a 6-gallon-per-minute pump. How long will it take to empty
the tank? Round your answer to the nearest minute. (Hint: Let x = the time the drain is open.)
21. Quiet Living Rentals rents efficiency apartments for $375 per month, 1-bedroom apartments for $500
per month, and 2-bedroom apartments for $625 per month. The business owns the same number of
1-bedroom as 2-bedroom apartments but four fewer efficiencies as 1- or 2-bedroom units. How many
of each does the business have if the rental income for one month is $16,500?
6.2 Graphing From the x- and y-Intercepts ~ 7
Solve the equations for the specified variable. 3.14
22. Ax + By = C for y
23. c = πd for π
24. d = kt 2 for t
Graph each of the equations using the x- and y-intercepts or origin and slope. 6.2
25. 3x + y = 4
26. x + 2y = –3
27. 3x – y = 2
28. x – 2y = 0
Extra Practice
Graph each of the equations using the x- and y-intercepts or origin and slope. 6.2
29. 3x + 5y = –15
30. –7x + 4y = 28
8 ~ Algebra I Unit 6
31. 10x + 22y = 55
32. 12x + 7y = – 42
6.3
Factoring Perfect Square Trinomials
Lesson 4.14 taught squaring a binomial by using the square-double-square method. This formed
a perfect square trinomial.
(y + 7)2 = y 2 + 14y + 49
Notice these two characteristics of perfect square trinomials:
1. The first and last terms of the trinomial are perfect squares.
y 2 + 14y + 49
2. The middle term is the square root of each outer term multiplied and then doubled.
y 2 + 14y + 49
(y • 7) • 2
Any trinomial having these characteristics is a perfect square trinomial and can be factored into
two identical binomials, which can be written as a binomial squared.
To Factor a Perfect Square Trinomial
1. Write a parentheses squared.
2. Write the square root of the first trinomial term.
3. Write the sign of the middle term of the trinomial.
4. Write the square root of the last trinomial term.
Example 1. Factor the trinomial x 2 – 16x + 64.
x 2 – 16x + 64
(
(x
)2
)2
(x – )2
(x – 8)2
Original trinomial.
A parentheses squared written.
√x 2 used for the first binomial term.
Sign of middle term of the trinomial written.
√64 used for the second binomial term.
6.3 Factoring Perfect Square Trinomials ~ 9
Example 2. Factor the trinomial 4b 2 + 12b + 9.
4b 2 + 12b + 9
Original trinomial.
(2b
√4b 2 used for the first binomial term.
(
)
(2b +
)2
A parentheses squared written.
2
)2
Sign of middle term of the trinomial written.
√9 used for the second binomial term.
(2b + 3)2
Example 3. Factor the trinomial y 2 + 12y + 49.
This is not a perfect square trinomial. Doubling the product of the outer terms’ square
roots 2 (y • 7) gives 14y, not 12y.
Factor the trinomials. If any is not a perfect square, write not a perfect square. 6.3
1. x 2 – 6x + 9
2. x 2 + 15x + 49
3. x 2 – 2x + 1
7. x 4 + 4x 2 + 4
8. 9x 2 – 24x + 16
9. x 2 – 2xy + y 2
4. 4x 2 – 4x + 1
5. 9 + 6x + x 2
Review
6. x 2 – 8x + 25
Graph each of the equations using the x- and y-intercepts. 6.2
10. 7x + 2y = 14
12. x + y = 2
11. 3x – 5y = 15
Solve the inequalities. 5.7
14. –
x
≤4
3
13. 7x – 2y = –14
15. – 9x – 11 < 37 – 3x
16. 7x < 4 – x
Label the systems as dependent, inconsistent, or consistent. 6.1
17.
y
18.
x
10 ~ Algebra I Unit 6
y
x
19.
y
x
Use the five steps to set up and solve the equations. 4.1
20. Mark invested in the kingdom of God through an offering to two different missions totaling $2,700. If
the offering to the second mission was 80% of that for the first, what were the individual amounts?
a) first mission = (x)
Simplify the radicals if possible. 5.3
21. √5,000
3
22. √147
Follow the directions. 5.14 Use an actual paper and scissors to help see
how this works.
24. Gail had a square piece of cardboard that was x inches long on each
side. From a corner, she cut a 3 in square. Thus the area left over was
x 2 – 32. Factor this binomial.
25. Gail cut along the diagonal that is indicated by the dashed line. She
then flipped one piece over and rearranged the pieces to make a
rectangle as shown. Which of the factors found in the previous
problem represents the length of this rectangle? Which of the factors
found in the previous problem represents the width of this rectangle?
23. √112
3
3
x
x
3
x
x
3
Draw solution graphs for these compound inequalities. 4.11
26. –3 ≤ x < 30
27. x < –1 or x > 1
28. (6x 2 – 4xy + 3y – 1) + (4y 2 – 2xy – 7)
29. (2r 2 + 3s – s 2) + (–s 2 – 4s – 7)
Add the polynomials. 3.4
Use the five steps to set up and solve the equations. 5.13
30. A radiator holds 16 quarts of liquid—a mixture of antifreeze and water. If the amount of antifreeze is
2 quarts less than the quarts of water, how many quarts of each is there in the radiator?
a) amount of water = (x)
31. Marcus began filling his 5,000-gallon swimming pool with his household hose at a rate of 7 gallons
per minute. 90 minutes later his neighbor came home and added his hose with a capacity of 6 gallons
per minute. If Marcus began filling the pool at 9:00 a.m., when would the pool be filled? Round to the
nearest minute.
Simplify the binomials mentally (square-double-square). 4.14
32. (x + 9)2
33. (3 + 5y)2
34. (2x – 2y)2
Factor the trinomials. If any is not a perfect square, write not a perfect square. 6.3
35. x 2 + 3x + 1
36. 9x 4 + 30x 2 + 25
37. 49x 2 – 98x + 49
6.3 Factoring Perfect Square Trinomials ~ 11