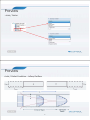
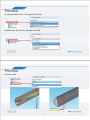
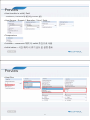
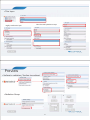
* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download COMSOL Multiphysics Training
Survey
Document related concepts
Transcript
COMSOL Multiphysics Training ≷⋗ờ Ệ῭ᵙ⋘ ࢄࠤ෮ঃଡਏ࢘ߑଲ׆ୢր୨ଡCOMSOL Multiphysics ֻවॷୀഉൾଲਆ(6* ࠜଲਓசߦෘۗۍ INDEX 1. Introduction/ 01 2. Natural Convection Cooling of a Vacuum Flask / 3. Droplet Breakup in a T-Junction / 4. Cooling of an Injection Mold / 69 5. Electroosmotic Micromixer / 97 6. Fluid-Structure Interaction / 125 48 07 Introduction 1 COMSOLV5.0ProductSuite HeatTransferModule • &RQGXFWLRQFRQYHFWLRQDQGUDGLDWLRQ • 5DGLDWLRQ 6XUIDFHWRVXUIDFH6XUIDFHWRDPELHQW ([WHUQDO5DGLDWLRQ6RXUFH 6XQ5DGLDWLRQ 0XOWL:DYHOHQJWK+HDW5DGLDWLRQ • (DV\WRXVHIRUPRGHOLQJDSKDVHFKDQJH RIPDWHULDOV • $GG0RLVWDLUIOXLGW\SH • %LRKHDW • 7KHUPDOFRQWDFW • (DV\WRHYDOXDWHIRUKHDWDQGHQHUJ\ EDODQFH 2 CFDModule • 0RGHOODPLQDUDQGWXUEXOHQWIORZVLQVLQJOHRUPXOWL SKDVHV • 6LPXODWLRQLQWKHIUHHDQGSRURXVPHGLDIORZ • 5HDG\FRXSOLQJRIKHDWDQGPDVVWUDQVSRUWWRIOXLG IORZ KHDWH[FKDQJHUVWXUELQHVVHSDUDWLRQVXQLWVDQG YHQWLODWLRQV\VWHPV • 7KLQILOPIORZIRUFDYLWDWLRQ • &UHHSLQJIORZDWVPDOO5H\QROGVQXPEHUVLQYHU\ VPDOOFKDQQHOV • ,QWHULRU:DOO • :DOO5RXJKQHVVNƃNZPRGHO Comparisionofturbulencemodels low Re k-epsilon, 32 min 16 sec k-epsilon, 9 min 13 sec Algebraic yPlus, 2 min 44 sec • Algebraic yPlus and L-VEL • Spalart-Allmaras • k-epsilon • k-omega • low Re k-epsilon • SST +PETGCKPI%QORWVCVKQPCNEQUV 3 MixerModule • Impeller and a vessel in containing machinery-based mixers • Used in many industrial processes, such as the production of consumer products, pharmaceuticals, food, and fine chemicals. • Free surface • Add-on to the CFD Module MicrofluidicsModule • Easy-to-use tools for the study microfluidic devices and rarefied gas flows. • Set up to coupled electrokinetic and magnetodynamic simulations easily including electrophoresis, magnetophoresis, dielectrophoresis, electroosmosis, and electrowetting. • Slip flow Analysis 4 SubsurfaceFlowModule • Model single and coupled processes related to subsurface flow • Oil and gas flow in porous media, the modeling of groundwater flow, and the spread of pollution through soil PipeFlowModule • Flow, heat, and mass transport in pipe networks. • Two-Phase Flow(JDVOLTXLGPL[WXUHV in Pipes • 9HORFLW\SUHVVXUHYDULDWLRQ WHPSHUDWXUH • 'OLQHVRUFXUYHVHPEHGGHGLQ' RU'Podel. • Pipe connection node • 3LSLQJFRPSRQHQWVVXFKDV%HQG 9DOYHV3XPSV7MXQFWLRQV 5 MolecularModule • $SSOLHVWRWKHWUDQVLWLRQDOIORZDQGIUHH PROHFXODUIORZUHJLPHV. • )DVWFRPSXWDWLRQVRIVWHDG\VWDWHIUHH PROHFXODUIORZZLWK$QJXODU&RHIILFLHQW 0HWKRG • 'HVLJQDQGVLPXODWLRQRIYDFXXP V\VWHPV • $GVRUSWLRQGHVRUSWLRQDQGGHSRVLWLRQ ParticleTracingModule • Compute trajectories of particles in a fluid or an electromagnetic field. - Including particle-field interactions, particleparticle interaction force. • Mixinginastaticmixer Predefined force: Electric, Magnetic, Drag, Brownian, gravity, Dielectrophoretic, Magnetoph-oretic, and so on. • Wall boundary condition: Freeze, Stick, Bounce, Disappear, Diffuse reflection, and General reflection. 6 Natural Convection Cooling of a Vacuum Flask 7 NaturalConvectionCoolingofaVacuumFlask 3UHYLHZ FluidFlow Porous Smallpores Saturated «Darcy» Free Largepores «Brinkman» Unsaturated «Richards» Laminar «NavierͲStokes» Newtonian 8 NonͲNewtonian Turbulent «RANS» 3UHYLHZ • Inlet/Outlet 3UHYLHZ • Inlet/OutletCondition– Inflow,Outflow 9 3UHYLHZ • Incompressibleflow/Compressibleflow • Newtonianfluid/NonͲNewtonianfluid 3UHYLHZ • Interiorwall nothickness 10 3UHYLHZ • Heattransferinsolid/fluid Ͳ Conduction/Convection߾ ଥкଜЕ Domain۶ࢽ • HeatSourceͲ Domain/Boundary/Line/Point • Temperature • Outflow– Convectionଥ۱ ݤoutlet࣏ʢࡳԻ ࡈی • Initialvalues– ݤɾ ଥ۱ ݤট̛ ࠟѦ ʅ ۶ࢽ ࣸࡁ 3UHYLHZ • HeatFlux 11 • ThinLayer Highlyconductivelayer ThinThermallyResistiveLayer 3UHYLHZ • Surfacetoradiation/Surfacetoambient • RadiationGroup 12 3UHYLHZ • HeatBalance(Globalvariables) dEiInt ntfluxInt QInt WnsInt • EnergyBalance(Globalvariables) dEi0Int ntefluxInt 13 QInt WInt Model Firstapproach Convectionheattransfercoefficient(h) withoutlaminarorturbulentflow Flask Secondapproach Convectiveflowofair Physics 1.Heattransferinsolid HeatTransferequation Convectiveheattransfercoefficientfornaturalconvectioninaironaverticalheatedwalland inclinedandhorizontalplane(RaL andPr areRayleighandPrandtl dimensionlessnumber) Nusselt number 2.Conjugateheattransfer=Laminarflow+Heattransferinsolid NavierͲstokesequation Rayleighnumber Volumeforcedefinedbybuoyancyforce g:gravity(m/s^2) N:thermaldiffusivity(m^2/s) T:temperature(K) h:heightofaconvectionobject(m) ɲ:coefficientofthermalexpansion(1/K) ʆ:kinematicviscosity(m^2/s) g:gravity(m/s^2) ʌ:density ʌ:referencedensityatatmosphere pressureand25C 14 Material/Boundarycondition Conductivity(W/(mͼK) Density(Kg/m^3) HeatCapacityJ/(kgͼK) Form 0.03 60 200 Nylon 0.26 1150 1700 Steel AISI4340 44.5 7850 475 Assumption:Noconnectiveflowincoffeeandithasaconstanttemperatureof90C Boundarycondition Wetsurfaceofastainlesssteelshell:90C Bottomarea:insulated(zeroflux) Ambienttemperature:25C 5HVXOW 15 Solved with COMSOL Multiphysics 5.0 Natural Convection Cooling of a Vacuum Flask Introduction This example solves a pure conduction problem and a free-convection problem in which a vacuum flask holding hot coffee dissipates thermal energy. The main interest is to calculate the flask’s cooling power; that is, how much heat it loses per unit time. Figure 1: Schematic picture of the flask (left) and velocity streamlines in the flask model including flow simulation. This example uses two different approaches to model natural convection cooling: • Using heat transfer coefficients to describe the thermal dissipation • Modeling the convective flow of air outside the flask to describe the thermal dissipation The first approach describes the outside heat flux using a heat transfer coefficient function from the Heat Transfer Coefficients library included with the Heat Transfer Module. This results in a rather simple model that predicts the stationary cooling well and produces accurate results for temperature distribution and cooling power. 1 | NATURAL CONVECTION COOLING OF A VACUUM FLASK 16 Solved with COMSOL Multiphysics 5.0 The second approach solves for both the total energy balance and the flow equations of the outside cooling air. This model version produces detailed results for the flow field around the flask as well as for the temperature distribution and cooling power. However, it is more complex and requires more computational resources than the first version. Model Definition Figure 2 shows the model geometry. Figure 2: A 3D cut-away drawing (inset) of the flask with coffee; a stainless-steel shell (light gray) that can be filled with an insulating material such as foam; an insulating ring around the flask neck (black); and a screw stopper (dark gray). The 2D-axisymmetric representation appears on the right. C O N T R O L VO L U M E For the first approach, the model does not include a control volume around the flask to represent the domain of the surrounding air. Instead, it uses a heat transfer coefficient correlation to simulate the surrounding air in the vertical and horizontal plates. For the second approach, the model uses a control volume around the flask to represent the domain of the surrounding air. Choosing an appropriate control volume for natural convection models is difficult. Your choice strongly influences the model, the mesh, the convergence, and especially the flow behavior. The real-world air domain surrounding the 2 | N A T U R A L C O NVE C T I O N C O O L I N G O F A VA C U U M F L A S K 17 Solved with COMSOL Multiphysics 5.0 flask is the entire room or atmosphere in which the flask is placed. Making the rectangle as large as the external room would result in a very large model requiring a supercomputer to solve. At the other extreme, if you make the control volume too small, the solution is affected by the imposed artificial boundary conditions, and there can also be a truncation of flow eddies, making convergence difficult. An appropriate truncation should resolve the flow field around the flask but avoid modeling a large surrounding. One way to approach this task is to start with a small control volume, set up and solve the model, then expand the control volume, solve the model again, and see if the results change. This example uses a sufficiently large control volume by truncating the air domain at r 0.1 m and z 0.5 m. The boundary condition at the boundaries that are open to large volumes can handle both entering and leaving fluid. The entering fluid has the temperature of the surroundings whereas the leaving fluid has an unknown temperature that results from the cooling effects of the flow field. MATERIAL PROPERTIES Next consider the materials that make up the flask model. The screw stopper and insulation ring are made of nylon. The flask bottle consists of stainless steel, and the filling material between the inner and outer walls is a plastic foam. The material library includes all materials used in this model except the foam, which you specify manually. Table 1 provides a list of standard foam’s thermal properties. TABLE 1: FOAM MATERIAL PROPERTIES PROPERTY VALUE Conductivity 0.03 W/(m·K) Density 60 kg/m3 Heat Capacity 200 J/(kg·K) H E A T TR A N S F E R P H Y S I C S This example neglects the convective flow in the hot liquid (coffee). The thermal conductivity in the liquid is large enough to make the temperature gradients rather small. The study assumes that the flask is thermally stationary, although a real flask continuously loses heat and cools down. Because the heat-loss process in the hot liquid is slow compared to the convective flow, a quasi-stationary model assuming that the coffee has a constant temperature of 90 °C (363.15 K) is applicable. Such a model reveals the temperature gradients and cooling power. The model results show where the main losses appear, and thus where improvements are possible—which is what a flask designer is really interested in. 3 | NATURAL CONVECTION COOLING OF A VACUUM FLASK 18 Solved with COMSOL Multiphysics 5.0 Approach 1—Loading a Heat Transfer Coefficient Function This model version uses a simplified approach and solves the stationary thermal-conduction equation making use of a heat transfer coefficient, h, to describe the natural convection cooling on the outside surfaces of the flask. This approach is very powerful in many situations, especially if the main interest is not the flow behavior but rather its cooling power. By using the appropriate h correlations, you can generally arrive at accurate results at a very low computational cost. In addition, many correlations are valid for the entire flow regime, from laminar to turbulent flow. This makes it possible to approach the problem directly without predicting whether the flow is laminar or turbulent. BOUNDARY CONDITIONS Vertical boundaries along the axis of symmetry have a symmetry condition (zero gradients, set by COMSOL Multiphysics automatically); the wet surface of the stainless-steel shell is held at a constant temperature of 90 °C; the bottom is modeled as perfectly insulated (zero flux). The flask surfaces are exposed to air and are cooled by convection. The use of a highly conductive layer feature models the thickness of the steel shell. The only remaining energy-balance boundary condition is for the flask surface. In the first approach a convective heat-transfer coefficient together with the ambient temperature, 25 °C, describes the heat flux. C O NVE C T I VE H E A T TR A N S F E R C O E F F I C I E N T The outer surfaces dissipate heat via natural convection. This loss is characterized by the convective heat transfer coefficient, h, which in practice you often determine with empirical handbook correlations. Because these correlations depend on the surface temperature, Tsurface, engineers must estimate Tsurface and then iterate between h and Tsurface to obtain a converged value for h. Most of these correlations require tedious computations and property interpolations that make this iterative process quite unpleasant and labor intensive. A typical handbook correlation (see Ref. 1) for h for the case of natural convection in air on a vertical heated wall RaLd109 is k Nu L h = ------------------L 0.670Ra L1 / 4 NuL = 0.68 + ----------------------------------------------------0.492 9 / 16 4 / 9 1 + §© ---------------·¹ Pr 4 | N A T U R A L C O NVE C T I O N C O O L I N G O F A VA C U U M F L A S K 19 Solved with COMSOL Multiphysics 5.0 where RaL and Pr are the Rayleigh and Prandtl dimensionless numbers. A similar relation involving Nusselt numbers holds for inclined and horizontal planes (see The Heat Transfer Coefficients for details). COMSOL Multiphysics handles these types of nonlinearities internally and adds much convenience to such computations, so there is no need to iterate. The Heat Transfer Module provides heat transfer coefficient functions that you can access easily in the Convective Heat Flux feature. Approach 2—Modeling the External Flow Another approach for simulating the cooled flask is to produce a model that computes the convective velocity field around the flask in detail. Before proceeding with a simulation of this kind, it is a good idea to try to estimate the Rayleigh number because that number influences the choice between assuming laminar flow and applying a turbulence model. The Rayleigh number describes the ratio between buoyancy and viscous forces in free convection problems. It is defined as 3 gD'Th Ra = ---------------------NQ with g as the gravity (SI unit: m/s2), Nthe thermal diffusivity (SI unit: m2/s), 'T the Temperature difference (SI unit: K), h the height of the convective object (SI unit: m), D the coefficient of thermal expansion (SI unit: 1/K), and Q the kinematic viscosity (SI unit: m2/s). The model’s length scale is the length of the heated fluid’s flow path, in this example 0.5 m. Notice that this value increases if the modeled flow domain is extended in the direction of the flow. 'T is about 15 K (assuming that the flask surface temperature is 15 °C above the ambient temperature). Together with the material properties of air at atmospheric pressure and T about 25 °C the result is below 1·109, which indicates that the flow is still laminar rather than turbulent. Thus, it makes sense to model the flow using a physics interface for laminar flow. BUOYANCY-DRIVEN FLOW To model non-isothermal buoyancy-driven flow, the following example uses COMSOL Multiphysics’ Conjugate Heat Transfer interface. It provides a generalized Navier-Stokes formulation that takes varying density into account as well as the energy equation. The buoyancy forces are included by specifying a volume force in this way 5 | NATURAL CONVECTION COOLING OF A VACUUM FLASK 20 Solved with COMSOL Multiphysics 5.0 F = U – U ref g with grz 09.81 m/s2, Uthe density and Uref the reference density at atmospheric pressure and 25 °C. BOUNDARY CONDITIONS When solving flow problems numerically, your engineering intuition is crucial in setting good boundary conditions. In this problem, the warm flask drives vertical air currents along its walls, and they eventually join in a thermal plume above the top of the flask. Air is pulled from the surroundings toward the flask where it eventually feeds into the vertical flow. The open boundary condition is a boundary condition for the heat and flow equation and can handle incoming flow with ambient temperature and leaving flow with a-priori unknown temperature. You would expect this flow to be quite weak and therefore do not anticipate any significant changes in dynamic pressure. Flow Boundary Conditions • On the top and right boundaries, the normal stress is zero as an open boundary with ambient temperature of 25 °C. • On the upper-left boundary, the flow domain coincides with the axis of symmetry where the Axial Symmetry condition is applied automatically. • All other boundaries (the flask surface and the bottom horizontal line) are walls where you use the No slip condition. Thermal Boundary Conditions • The top and right boundaries are the exit and entrance of the flow domain respectively where convection dominates; accordingly, use an open boundary condition. • Again, the top left is described by axial symmetry, which is set by default. • Assume that the bottom is perfectly insulated. All other boundaries (the flask surface) have continuity in temperature and flux by default. 6 | N A T U R A L C O NVE C T I O N C O O L I N G O F A VA C U U M F L A S K 21 Solved with COMSOL Multiphysics 5.0 Results and Discussion Figure 3 shows the temperature distribution in both the flask and the surrounding air. However, the temperature results in the solid parts are close to identical for the case of modeling with a heat transfer coefficient. Figure 3: Temperature results for the model including the fluid flow. The main interest with the model is to calculate the integral cooling power, which indicates how long the coffee stays hot. Both approaches give a total cooling power of about 6 W±1 W. Focusing on this value the first approach provides accurate results. 7 | NATURAL CONVECTION COOLING OF A VACUUM FLASK 22 Solved with COMSOL Multiphysics 5.0 A second question concerns how the cooling power is distributed on the flask surface. The heat transfer coefficient represents this property. Figure 4 shows a comparison of the predicted distribution of h along the height of the flask between the two models. Figure 4: Heat transfer coefficient along the vertical flask walls. Blue line: modeling approach using the heat transfer coefficient library, green line: modeling approach including the fluid flow. Figure 5 depicts the flow of air around the flask calculated from the flow model. This fluid flow model does a better job at describing local cooling power. 8 | N A T U R A L C O NVE C T I O N C O O L I N G O F A VA C U U M F L A S K 23 Solved with COMSOL Multiphysics 5.0 One interesting result is the vortex formed above the lid. It reduces the cooling in this region. Figure 5: Fluid velocity for air around the flask. CONCLUSIONS Using the Convective Heat Flux feature you can easily obtain simulation results. The predicted heat transfer coefficient is in the same range as the results from the model that includes the correlations, and the total cooling power is almost identical. However, the predefined heat transfer coefficients do not predict the local effects of air flow surrounding the flask. For this purpose, a flow model is more accurate. This means that you can use this type of model to create and calibrate functions for heat transfer coefficients for your geometries. Once calibrated, the functions allow you to use the first approach when solving large-scale and time-dependent models. Model Library path: Heat_Transfer_Module/ Tutorial_Models,_Forced_and_Natural_Convection/vacuum_flask 9 | NATURAL CONVECTION COOLING OF A VACUUM FLASK 24 Solved with COMSOL Multiphysics 5.0 Reference 1. F. Incropera, D. Dewitt, T. Bergman, and A. Lavine, Fundamentals of Heat and Mass Transfer, 6th ed., John Wiley & Sons, 2007. Modeling Instructions From the File menu, choose New. NEW 1 In the New window, click Model Wizard. MODEL WIZARD 1 In the Model Wizard window, click 2D Axisymmetric. 2 In the Select physics tree, select Heat Transfer>Heat Transfer in Solids (ht). 3 Click Add. 4 Click Study. 5 In the Select study tree, select Preset Studies>Stationary. 6 Click Done. GEOMETRY 1 The geometry sequence for the model is available in a file. If you want to create it from scratch yourself, you can follow the instructions in the Geometry Modeling Instructions section. Otherwise, insert the geometry sequence as follows: 1 On the Geometry toolbar, click Insert Sequence. 2 Browse to the model’s Model Library folder and double-click the file vacuum_flask_geom_sequence.mph. 3 In the Model Builder window, under Component 1 (comp1) right-click Geometry 1 and choose Build All Objects. You should now see the geometry shown in Figure 2. DEFINITIONS In the following section you define a few selections which will be needed during the model set up, for example the boundaries that represent the steel shell of the flask, the boundaries surrounding the hot coffee and the boundaries that are convectively cooled by the surrounding air. 10 | N A T U R A L C O NVE C T I O N C O O L I N G O F A VA C U U M F L A S K 25 Solved with COMSOL Multiphysics 5.0 Explicit 1 1 On the Definitions toolbar, click Explicit. 2 In the Settings window for Explicit, locate the Input Entities section. 3 From the Geometric entity level list, choose Boundary. 4 Select Boundaries 8–11, 13, and 16–21 only. 5 In the Label text field, type Shell. Explicit 2 1 On the Definitions toolbar, click Explicit. 2 In the Settings window for Explicit, locate the Input Entities section. 3 From the Geometric entity level list, choose Boundary. 4 Select Boundaries 4, 13, 17, and 20 only. 11 | NATURAL CONVECTION COOLING OF A VACUUM FLASK 26 Solved with COMSOL Multiphysics 5.0 5 In the Label text field, type Coffee boundaries. Explicit 3 1 On the Definitions toolbar, click Explicit. 2 In the Settings window for Explicit, locate the Input Entities section. 3 From the Geometric entity level list, choose Boundary. 4 Select Boundaries 14–16 and 21 only. 12 | N A T U R A L C O NVE C T I O N C O O L I N G O F A VA C U U M F L A S K 27 Solved with COMSOL Multiphysics 5.0 5 In the Label text field, type Flask, vertical wall. Parameters 1 In the Model Builder window, expand the Definitions node, then click Parameters. 2 In the Settings window for Parameters, locate the Parameters section. 3 In the table, enter the following settings: Name Expression Value Description T_amb 25[degC] 298.2 K Temperature of surrounding air T_coffee 90[degC] 363.2 K Coffee temperature d_shell 0.5[mm] 5.000E-4 m Steel-shell thickness p_amb 1[atm] 1.013E5 Pa Ambient pressure ADD MATERIAL 1 On the Model toolbar, click Add Material to open the Add Material window. 2 Go to the Add Material window. 3 In the tree, select Built-In>Air. 4 Click Add to Component in the window toolbar. 13 | NATURAL CONVECTION COOLING OF A VACUUM FLASK 28 Solved with COMSOL Multiphysics 5.0 MATERIALS Air (mat1) Leave the default geometric entity selection; subsequent materials that you add will override air as the material for the domains where it does not apply. ADD MATERIAL 1 Go to the Add Material window. 2 In the tree, select Built-In>Nylon. 3 Click Add to Component in the window toolbar. MATERIALS Nylon (mat2) 1 In the Model Builder window, under Component 1 (comp1)>Materials click Nylon (mat2). 2 Select Domains 3 and 4 only. ADD MATERIAL 1 Go to the Add Material window. 2 In the tree, select Built-In>Steel AISI 4340. 3 Click Add to Component in the window toolbar. 4 On the Model toolbar, click Add Material to close the Add Material window. MATERIALS Steel AISI 4340 (mat3) 1 In the Model Builder window, under Component 1 (comp1)>Materials click Steel AISI 4340 (mat3). 2 In the Settings window for Material, locate the Geometric Entity Selection section. 3 From the Geometric entity level list, choose Boundary. 4 From the Selection list, choose Shell. Material 4 (mat4) 1 In the Model Builder window, right-click Materials and choose Blank Material. 2 Select Domain 1 only. 3 In the Settings window for Material, locate the Material Contents section. 14 | N A T U R A L C O NVE C T I O N C O O L I N G O F A VA C U U M F L A S K 29 Solved with COMSOL Multiphysics 5.0 4 In the table, enter the following settings: Property Name Value Unit Property group Thermal conductivity k 0.03 W/ (m·K) Basic Density rho 60 kg/m³ Basic Heat capacity at constant pressure Cp 200 J/ (kg·K) Basic 5 In the Label text field, type Foam. H E A T TR A N S F E R I N S O L I D S ( H T ) The steel walls of the flask are represented by a special boundary condition for highly conductive layers: Thin Layer 1 1 On the Physics toolbar, click Boundaries and choose Thin Layer. 2 In the Settings window for Thin Layer, locate the Boundary Selection section. 3 From the Selection list, choose Shell. 4 Locate the Thin Layer section. From the Layer type list, choose Conductive. 5 In the ds text field, type d_shell. Temperature 1 1 On the Physics toolbar, click Boundaries and choose Temperature. 2 In the Settings window for Temperature, locate the Boundary Selection section. 3 From the Selection list, choose Coffee boundaries. 4 Locate the Temperature section. In the T0 text field, type T_coffee. This boundary condition partially overwrites the Thin Layer boundary condition. This is intentional because the conductivity of steel is high compared to the other materials in the model. The temperature can be assumed to be at coffee temperature throughout the steel layer in that part of the model. Heat Flux 1 1 On the Physics toolbar, click Boundaries and choose Heat Flux. 2 In the Settings window for Heat Flux, locate the Boundary Selection section. 3 From the Selection list, choose Flask, vertical wall. 4 Locate the Heat Flux section. Click the Convective heat flux button. 5 From the Heat transfer coefficient list, choose External natural convection. 15 | NATURAL CONVECTION COOLING OF A VACUUM FLASK 30 Solved with COMSOL Multiphysics 5.0 6 In the L text field, type height. 7 In the Text text field, type T_amb. Heat Flux 2 1 On the Physics toolbar, click Boundaries and choose Heat Flux. 2 Select Boundary 7 only. 3 In the Settings window for Heat Flux, locate the Heat Flux section. 4 Click the Convective heat flux button. 5 From the Heat transfer coefficient list, choose External natural convection. 6 From the list, choose Horizontal plate, upside. 7 In the L text field, type radius. 8 In the Text text field, type T_amb. MESH 1 1 In the Model Builder window, under Component 1 (comp1) click Mesh 1. 2 In the Settings window for Mesh, locate the Mesh Settings section. 3 From the Element size list, choose Extra fine. 4 Click the Build All button. STUDY 1 On the Model toolbar, click Compute. RESULTS Temperature, 3D (ht) A 3D temperature plot and an isothermal contour plot are produced by default. To display the temperatures in Celsius degrees, you can edit these existing plots: 1 In the Model Builder window, expand the Temperature, 3D (ht) node, then click Surface 1. 2 In the Settings window for Surface, locate the Expression section. 3 From the Unit list, choose degC. 4 On the 3D plot group toolbar, click Plot. Isothermal Contours (ht) 1 In the Model Builder window, expand the Isothermal Contours (ht) node, then click Contour 1. 2 In the Settings window for Contour, locate the Expression section. 16 | N A T U R A L C O NVE C T I O N C O O L I N G O F A VA C U U M F L A S K 31 Solved with COMSOL Multiphysics 5.0 3 From the Unit list, choose degC. 4 On the 2D plot group toolbar, click Plot. Approach 2 - Modeling the External Flow The second modeling approach can be done within the same MPH-file. Add a second model as follows: ROOT On the Model toolbar, click Add Component and choose 2D Axisymmetric. ADD PHYSICS 1 On the Model toolbar, click Add Physics to open the Add Physics window. 2 Go to the Add Physics window. 3 In the Add physics tree, select Heat Transfer>Conjugate Heat Transfer>Laminar Flow. 4 Find the Physics interfaces in study subsection. In the table, enter the following settings: Studies Solve Study 1 × 5 Click Add to Component in the window toolbar. 6 On the Model toolbar, click Add Physics to close the Add Physics window. ADD STUDY 1 On the Model toolbar, click Add Study to open the Add Study window. 2 Go to the Add Study window. 3 Find the Studies subsection. In the Select study tree, select Preset Studies>Stationary. 4 Find the Physics interfaces in study subsection. In the table, enter the following settings: Physics Solve Heat Transfer in Solids (ht) × This way, the new Study solves for the Conjugate Heat Transfer multiphysics interface only. Moreover, because the Deactivate added physics in other studies check-box is enabled, the Conjugate Heat Transfer multiphysics interface is disabled for Study 1. 5 Click Add Study in the window toolbar. 6 On the Model toolbar, click Add Study to close the Add Study window. 17 | NATURAL CONVECTION COOLING OF A VACUUM FLASK 32 Solved with COMSOL Multiphysics 5.0 Add a parameter that you will later use to ramp down the viscosity of air. DEFINITIONS Parameters 1 In the Model Builder window, under Global>Definitions click Parameters. 2 In the Settings window for Parameters, locate the Parameters section. 3 In the table, enter the following settings: Name Expression Value Description mu_factor 1 1.000 Factor for the air viscosity GEOMETRY 2 Import the geometry sequence defined for Component 1 as follows: Import 1 (imp1) 1 On the Model toolbar, click Import. 2 In the Settings window for Import, locate the Import section. 3 From the Geometry import list, choose Geometry sequence. 4 From the Source list, choose Geometry 1. 5 Click Import. In this approach, you model the fluid flow explicitly, so you need to add a flow domain to the model. Rectangle 1 (r1) 1 On the Geometry toolbar, click Primitives and choose Rectangle. 2 In the Settings window for Rectangle, locate the Size section. 3 In the Width text field, type 0.1[m]. 4 In the Height text field, type 0.5[m]. 5 Right-click Component 2 (comp2)>Geometry 2>Rectangle 1 (r1) and choose Build Selected. 6 Click the Zoom Extents button on the Graphics toolbar. Union 1 (uni1) 1 On the Geometry toolbar, click Booleans and Partitions and choose Union. 2 Click in the Graphics window and then press Ctrl+A to select all objects. 18 | N A T U R A L C O NVE C T I O N C O O L I N G O F A VA C U U M F L A S K 33 Solved with COMSOL Multiphysics 5.0 Split 1 (spl1) 1 On the Geometry toolbar, click Conversions and choose Split. 2 Select the object uni1 only. Delete Entities 1 (del1) 1 In the Model Builder window, right-click Geometry 2 and choose Delete Entities. 2 In the Settings window for Delete Entities, locate the Entities or Objects to Delete section. 3 From the Geometric entity level list, choose Domain. 4 On the object spl1(2), select Domain 1 only. 5 Click the Build All Objects button. DEFINITIONS Again, define selections which you can use during the model setup and for comparing the results of this approach to the first one. Explicit 4 1 On the Definitions toolbar, click Explicit. 2 In the Settings window for Explicit, locate the Input Entities section. 3 From the Geometric entity level list, choose Boundary. 4 Select Boundaries 10–13, 15, 18, and 21–25 only. Explicit 5 1 On the Definitions toolbar, click Explicit. 2 In the Settings window for Explicit, locate the Input Entities section. 3 From the Geometric entity level list, choose Boundary. 4 Select Boundaries 4, 15, 21, and 24 only. 5 In the Label text field, type Coffee boundaries. Explicit 6 1 On the Definitions toolbar, click Explicit. 2 In the Settings window for Explicit, locate the Input Entities section. 3 From the Geometric entity level list, choose Boundary. 4 Select Boundaries 16–18 and 25 only. 5 In the Label text field, type Flask vertical walls. 19 | NATURAL CONVECTION COOLING OF A VACUUM FLASK 34 Solved with COMSOL Multiphysics 5.0 MATERIALS You have added the materials in Model 1 already, you can now choose them from the Recent Materials folder in the Add Material window easily. ADD MATERIAL 1 On the Model toolbar, click Add Material to open the Add Material window. 2 Go to the Add Material window. 3 In the tree, select Recent Materials>Air. 4 Click Add to Component in the window toolbar. ADD MATERIAL 1 Go to the Add Material window. 2 In the tree, select Recent Materials>Nylon. 3 Click Add to Component in the window toolbar. MATERIALS Nylon (2) (mat6) 1 In the Model Builder window, under Component 2 (comp2)>Materials click Nylon (2) (mat6). 2 Select Domains 3 and 5 only. ADD MATERIAL 1 Go to the Add Material window. 2 In the tree, select Recent Materials>Steel AISI 4340. 3 Click Add to Component in the window toolbar. 4 On the Model toolbar, click Add Material to close the Add Material window. MATERIALS Steel AISI 4340 (2) (mat7) 1 In the Model Builder window, under Component 2 (comp2)>Materials click Steel AISI 4340 (2) (mat7). 2 In the Settings window for Material, locate the Geometric Entity Selection section. 3 From the Geometric entity level list, choose Boundary. 4 From the Selection list, choose Explicit 4. 20 | N A T U R A L C O NVE C T I O N C O O L I N G O F A VA C U U M F L A S K 35 Solved with COMSOL Multiphysics 5.0 Material 8 (mat8) 1 In the Model Builder window, right-click Materials and choose Blank Material. 2 Select Domain 1 only. 3 In the Settings window for Material, locate the Material Contents section. 4 In the table, enter the following settings: Property Name Value Unit Property group Thermal conductivity k 0.03 W/ (m·K) Basic Density rho 60 kg/m³ Basic Cp 200 J/ (kg·K) Basic Heat capacity at constant pressure 5 In the Label text field, type Foam. LAMINAR FLOW (SPF) 1 In the Model Builder window, under Component 2 (comp2) click Laminar Flow (spf). 2 Select Domain 4 only. 3 In the Settings window for Laminar Flow, locate the Domain Selection section. 4 Click Create Selection. 5 In the Create Selection dialog box, type Air in the Selection name text field. 6 Click OK. H E A T TR A N S F E R 2 ( H T 2 ) On the Physics toolbar, click Laminar Flow (spf) and choose Heat Transfer 2 (ht2). Heat Transfer in Fluids 1 The interface provides nodes for the solid and fluid domain by default and the remaining step is to assign the air domain to the Fluid node. Because the density depends on the temperature and the pressure, choose the calculated pressure as input for this material property. 1 In the Model Builder window, under Component 2 (comp2)>Heat Transfer 2 (ht2) click Heat Transfer in Fluids 1. 2 In the Settings window for Heat Transfer in Fluids, locate the Domain Selection section. 3 From the Selection list, choose Air. To get a good initial guess for the solver, set the initial value for the temperature to the ambient temperature. 21 | NATURAL CONVECTION COOLING OF A VACUUM FLASK 36 Solved with COMSOL Multiphysics 5.0 Initial Values 1 1 In the Model Builder window, under Component 2 (comp2)>Heat Transfer 2 (ht2) click Initial Values 1. 2 In the Settings window for Initial Values, locate the Initial Values section. 3 In the T2 text field, type T_amb. LAMINAR FLOW (SPF) On the Physics toolbar, click Heat Transfer 2 (ht2) and choose Laminar Flow (spf). Volume Force 1 1 On the Physics toolbar, click Domains and choose Volume Force. 2 Select Domain 4 only. 3 In the Settings window for Volume Force, locate the Volume Force section. 4 Specify the F vector as 0 r -g_const*(nitf1.rho-rho_ref) z The above steps define the buoyancy force acting on the air due to a density difference between the actual density nitf.rho and a reference density rho_ref, which is initially unknown and will be defined in the next step. DEFINITIONS Variables 1a 1 On the Model toolbar, click Variables and choose Local Variables. 2 In the Settings window for Variables, locate the Variables section. 3 In the table, enter the following settings: Name Expression Unit Description rho_ref mat5.def.rho(p_amb[ 1/Pa],T_amb[1/ K])[kg/m^3] kg/m³ Reference density for buoyancy force The above expression calls the density function of Material 5, which is air. The density depends on the temperature and pressure. Here the density will be evaluated for T = T_amb and p = p_amb, which are defined under the Global Definitions node. 22 | N A T U R A L C O NVE C T I O N C O O L I N G O F A VA C U U M F L A S K 37 Solved with COMSOL Multiphysics 5.0 H E A T TR A N S F E R 2 ( H T 2 ) Thin Layer 1 1 On the Physics toolbar, click Boundaries and choose Thin Layer. 2 In the Settings window for Thin Layer, locate the Boundary Selection section. 3 From the Selection list, choose Explicit 4. 4 Locate the Thin Layer section. From the Layer type list, choose Conductive. 5 In the ds text field, type d_shell. Temperature 1 1 On the Physics toolbar, click Boundaries and choose Temperature. 2 In the Settings window for Temperature, locate the Boundary Selection section. 3 From the Selection list, choose Coffee boundaries. 4 Locate the Temperature section. In the T0 text field, type T_coffee. Open Boundary 1 1 On the Physics toolbar, click Boundaries and choose Open Boundary. 2 Select Boundaries 9 and 20 only. 3 In the Settings window for Open Boundary, locate the Open Boundary section. 4 In the T0 text field, type T_amb. LAMINAR FLOW (SPF) 1 In the Model Builder window, under Component 2 (comp2) right-click Laminar Flow (spf) and choose Open Boundary. 2 Select Boundaries 9 and 20 only. MESH 2 Use finer meshes to get a good resolution of the flow field. 1 In the Model Builder window, under Component 2 (comp2) click Mesh 2. 2 In the Settings window for Mesh, locate the Mesh Settings section. 3 From the Element size list, choose Finer. 4 Click the Build All button. 23 | NATURAL CONVECTION COOLING OF A VACUUM FLASK 38 Solved with COMSOL Multiphysics 5.0 STUDY 2 Computing the flow for the fluid with low viscosity may introduce eddies in the flow field. Start computation using high viscosity to improve convergence. Use continuation feature to ramp down the viscosity. Step 1: Stationary 1 In the Model Builder window, under Study 2 click Step 1: Stationary. 2 In the Settings window for Stationary, click to expand the Study extensions section. 3 Locate the Study Extensions section. Select the Auxiliary sweep check box. 4 Click Add. 5 In the table, enter the following settings: Parameter name Parameter value list mu_factor 100 10 1 Parameter unit This factor must be multiplied with the air viscosity. MATERIALS Air (2) (mat5) 1 In the Model Builder window, under Component 2 (comp2)>Materials click Air (2) (mat5). 2 In the Settings window for Material, locate the Material Contents section. 3 In the table, enter the following settings: Property Name Value Unit Property group Dynamic viscosity mu eta(T[ 1/ K])[Pa *s]*mu _facto r Pa·s Basic STUDY 2 On the Model toolbar, click Compute. RESULTS Temperature, 3D (ht2) 1 In the Model Builder window, expand the Temperature, 3D (ht2) node, then click Surface 1. 24 | N A T U R A L C O NVE C T I O N C O O L I N G O F A VA C U U M F L A S K 39 Solved with COMSOL Multiphysics 5.0 2 In the Settings window for Surface, locate the Expression section. 3 From the Unit list, choose degC. 4 On the 3D plot group toolbar, click Plot. Isothermal Contours (ht2) This default plot shows the isothermal contours. Velocity (spf) This default plot shows the velocity magnitude in a 2D slice of the axisymmetric geometry. Pressure (spf) This default plot shows the pressure field in a 2D contour plot. 2D Plot Group 8 1 On the Model toolbar, click Add Plot Group and choose 2D Plot Group. 2 In the Settings window for 2D Plot Group, type Velocity, Streamlines in the Label text field. 3 Locate the Data section. From the Data set list, choose Study 2/Solution 2 (3). Velocity, Streamlines 1 Right-click Results>Velocity, Streamlines and choose Streamline. 2 In the Settings window for Streamline, click Replace Expression in the upper-right corner of the Expression section. From the menu, choose Component 2>Laminar Flow>u,w Velocity field. 3 Locate the Streamline Positioning section. From the Positioning list, choose Magnitude controlled. 4 Right-click Results>Velocity, Streamlines>Streamline 1 and choose Color Expression. 5 In the Settings window for Color Expression, click Replace Expression in the upper-right corner of the Expression section. From the menu, choose Component 2>Laminar Flow>spf.U - Velocity magnitude. 6 On the 2D plot group toolbar, click Plot. For the comparison of temperatures along the outer vertical walls of the vacuum flask (Figure 6), plot the solutions of approach 1 and 2 in one plot group. The solutions are stored under the Data Sets node and for each plot one can choose which Data Set should be used. 1D Plot Group 9 1 On the Model toolbar, click Add Plot Group and choose 1D Plot Group. 2 On the 1D plot group toolbar, click Line Graph. 25 | NATURAL CONVECTION COOLING OF A VACUUM FLASK 40 Solved with COMSOL Multiphysics 5.0 3 In the Settings window for Line Graph, locate the Selection section. 4 From the Selection list, choose Flask, vertical wall. 5 Locate the y-Axis Data section. From the Unit list, choose degC. 6 Locate the x-Axis Data section. From the Parameter list, choose Expression. 7 In the Expression text field, type z. 8 Click to expand the Legends section. Select the Show legends check box. 9 From the Legends list, choose Manual. 10 In the table, enter the following settings: Legends No flow 11 On the 1D plot group toolbar, click Line Graph. 12 In the Settings window for Line Graph, locate the Data section. 13 From the Data set list, choose Study 2/Solution 2 (3). 14 From the Parameter selection (mu_factor) list, choose Last. 15 Locate the Selection section. From the Selection list, choose Flask vertical walls. 16 Locate the y-Axis Data section. In the Expression text field, type T2. 17 From the Unit list, choose degC. 18 Locate the x-Axis Data section. From the Parameter list, choose Expression. 19 In the Expression text field, type z. 20 Locate the Legends section. Select the Show legends check box. 21 From the Legends list, choose Manual. 22 On the 1D plot group toolbar, click Plot. 23 In the table, enter the following settings: Legends With flow 24 In the Model Builder window, click 1D Plot Group 9. 25 In the Settings window for 1D Plot Group, type Temperature vacuum flask in the Label text field. 26 | N A T U R A L C O NVE C T I O N C O O L I N G O F A VA C U U M F L A S K 41 Solved with COMSOL Multiphysics 5.0 The plot should look like that shown in the figure below. Figure 6: Temperature distribution along the outer vertical walls of the flask. Blue line: modeling approach using the heat transfer coefficient library. Green line: modeling approach including the fluid flow. To compare the heat transfer coefficients for the two modeling approaches (Figure 4), do the following: 1D Plot Group 10 1 On the Model toolbar, click Add Plot Group and choose 1D Plot Group. 2 On the 1D plot group toolbar, click Line Graph. 3 In the Settings window for Line Graph, locate the Selection section. 4 From the Selection list, choose Flask, vertical wall. 5 Locate the y-Axis Data section. In the Expression text field, type ht.hf1.h. 6 Locate the x-Axis Data section. From the Parameter list, choose Expression. 7 In the Expression text field, type z. 8 Locate the Legends section. Select the Show legends check box. 9 From the Legends list, choose Manual. 27 | NATURAL CONVECTION COOLING OF A VACUUM FLASK 42 Solved with COMSOL Multiphysics 5.0 10 In the table, enter the following settings: Legends Heat transfer coefficient, no flow 11 On the 1D plot group toolbar, click Line Graph. 12 In the Settings window for Line Graph, locate the Data section. 13 From the Data set list, choose Study 2/Solution 2 (3). 14 From the Parameter selection (mu_factor) list, choose Last. 15 Locate the Selection section. From the Selection list, choose Flask vertical walls. 16 Locate the y-Axis Data section. In the Expression text field, type abs(ht2.ntflux)/ (T2-T_amb). 17 Locate the x-Axis Data section. From the Parameter list, choose Expression. 18 In the Expression text field, type z. 19 Locate the Legends section. Select the Show legends check box. 20 From the Legends list, choose Manual. 21 In the table, enter the following settings: Legends Calculated heat transfer coefficient, with flow 22 In the Model Builder window, click 1D Plot Group 10. 23 In the Settings window for 1D Plot Group, type Heat transfer coefficient in the Label text field. Derived Values Finally, calculate the integral cooling power. 1 On the Results toolbar, click More Derived Values and choose Integration>Line Integration. 2 Select Boundaries 7, 14–16, and 21 only. 3 In the Settings window for Line Integration, click Replace Expression in the upper-right corner of the Expression section. From the menu, choose Component 1>Heat Transfer in Solids>Boundary fluxes>ht.ntflux - Normal total heat flux. 4 Locate the Integration Settings section. Select the Compute surface integral check box. 5 Click the Evaluate button. 28 | N A T U R A L C O NVE C T I O N C O O L I N G O F A VA C U U M F L A S K 43 Solved with COMSOL Multiphysics 5.0 6 On the Results toolbar, click More Derived Values and choose Integration>Line Integration. 7 In the Settings window for Line Integration, locate the Data section. 8 From the Data set list, choose Study 2/Solution 2 (3). 9 From the Parameter selection (mu_factor) list, choose Last. 10 Select Boundaries 8, 16–18, and 25 only. 11 Locate the Expression section. In the Expression text field, type ht2.ntflux. 12 Locate the Integration Settings section. Select the Compute surface integral check box. 13 Click the Evaluate button. TABL E 1 Go to the Table window. The results are displayed in the Table window below the Graphics window. Geometry Modeling Instructions If you wish to create the geometry yourself, follow these steps. On the Model toolbar, click Add Component and choose 2D Axisymmetric. DEFINITIONS Parameters 1 On the Model toolbar, click Parameters. 2 In the Settings window for Parameters, locate the Parameters section. 3 In the table, enter the following settings: Name Expression Value Description height 380[mm] 0.38000 m Flask height radius 40[mm] 0.040000 m Bottleneck radius GEOMETRY 1 Bézier Polygon 1 (b1) 1 On the Geometry toolbar, click Primitives and choose Bézier Polygon. 2 In the Settings window for Bézier Polygon, locate the Polygon Segments section. 3 Find the Added segments subsection. Click Add Linear. 4 Find the Control points subsection. In row 2, set r to 1.5*radius. 29 | NATURAL CONVECTION COOLING OF A VACUUM FLASK 44 Solved with COMSOL Multiphysics 5.0 5 Find the Added segments subsection. Click Add Linear. 6 Find the Control points subsection. In row 2, set z to 0.68*height. 7 Find the Added segments subsection. Click Add Quadratic. 8 Find the Control points subsection. In row 2, set z to 0.751*height. 9 In row 3, set r to 1.04*radius, and z to 0.80*height. 10 Find the Added segments subsection. Click Add Quadratic. 11 Find the Control points subsection. In row 2, set r to 0.88*radius. 12 In row 2, set z to 0.82*height. 13 In row 3, set r to 0.66*radius and z to 0.84*height. 14 Find the Added segments subsection. Click Add Linear. 15 Find the Control points subsection. In row 2, set z to 0.96*height. 16 Find the Added segments subsection. Click Add Linear. 17 Find the Control points subsection. In row 2, set r to 0.3*radius. 18 Find the Added segments subsection. Click Add Linear. 19 Find the Control points subsection. In row 2, set z to 0.83*height. 20 Find the Added segments subsection. Click Add Linear. 21 Find the Control points subsection. In row 2, set z to 0.79*height. 22 Find the Added segments subsection. Click Add Quadratic. 23 Find the Control points subsection. In row 2, set r to 0.56*radius. 24 In row 2, set z to 0.78*height. 25 In row 3, set r to 0.73*radius and z to 0.75*height. 26 Find the Added segments subsection. Click Add Quadratic. 27 Find the Control points subsection. In row 2, set r to 0.93*radius. 28 In row 2, set z to 0.72*height. 29 In row 3, set r to 0.93*radius and z to 0.68*height. 30 Find the Added segments subsection. Click Add Linear. 31 Find the Control points subsection. In row 2, set z to 0.12*height. 32 Find the Added segments subsection. Click Add Quadratic. 33 Find the Control points subsection. In row 2, set z to 0.036*height. 34 In row 3, set r to 0*radius and z to 0.036*height. 30 | N A T U R A L C O NVE C T I O N C O O L I N G O F A VA C U U M F L A S K 45 Solved with COMSOL Multiphysics 5.0 35 Right-click Component 1 (comp1)>Geometry 1>Bézier Polygon 1 (b1) and choose Build Selected. Rectangle 1 (r1) 1 On the Geometry toolbar, click Primitives and choose Rectangle. 2 In the Settings window for Rectangle, locate the Size section. 3 In the Width text field, type 1.04*radius. 4 In the Height text field, type 0.16*height. 5 Locate the Position section. In the z text field, type 0.83*height. Rectangle 2 (r2) 1 On the Geometry toolbar, click Primitives and choose Rectangle. 2 In the Settings window for Rectangle, locate the Size section. 3 In the Width text field, type 0.74*radius. 4 In the Height text field, type 0.13*height. 5 Locate the Position section. In the r text field, type 0.3*radius. 6 In the z text field, type 0.83*height. Difference 1 (dif1) 1 On the Geometry toolbar, click Booleans and Partitions and choose Difference. 2 Select the object r1 only. 3 In the Settings window for Difference, locate the Difference section. 4 Find the Objects to subtract subsection. Select the Active toggle button. 5 Select the object r2 only. Bézier Polygon 2 (b2) 1 On the Geometry toolbar, click Primitives and choose Bézier Polygon. 2 In the Settings window for Bézier Polygon, locate the Polygon Segments section. 3 Find the Added segments subsection. Click Add Quadratic. 4 Find the Control points subsection. In row 1, set r to 1.04*radius. 5 In row 1, set z to 0.80*height. 6 In row 2, set r to 0.88*radius and z to 0.82*height. 7 In row 3, set r to 0.66*radius and z to 0.84*height. 8 Find the Added segments subsection. Click Add Linear. 9 Find the Control points subsection. In row 2, set z to 0.96*height. 31 | NATURAL CONVECTION COOLING OF A VACUUM FLASK 46 Solved with COMSOL Multiphysics 5.0 10 Find the Added segments subsection. Click Add Linear. 11 Find the Control points subsection. In row 2, set r to 1.04*radius. 12 Find the Added segments subsection. Click Add Linear. 13 Find the Control points subsection. In row 2, set z to 0.80*height. Bézier Polygon 3 (b3) 1 On the Geometry toolbar, click Primitives and choose Bézier Polygon. 2 In the Settings window for Bézier Polygon, locate the Polygon Segments section. 3 Find the Added segments subsection. Click Add Linear. 4 Find the Control points subsection. In row 1, set r to 0.3*radius. 5 In row 1, set z to 0.83*height. 6 In row 2, set r to 0.3*radius and z to 0.79*height. 7 Find the Added segments subsection. Click Add Quadratic. 8 Find the Control points subsection. In row 2, set r to 0.56*radius. 9 In row 2, set z to 0.78*height. 10 In row 3, set r to 0.73*radius and z to 0.75*height. 11 Find the Added segments subsection. Click Add Linear. 12 Find the Control points subsection. In row 2, set r to 0*radius. 13 Find the Added segments subsection. Click Add Linear. 14 Find the Control points subsection. In row 2, set z to 0.83*height. 15 Click the Build All Objects button. 32 | N A T U R A L C O NVE C T I O N C O O L I N G O F A VA C U U M F L A S K 47 Droplet Breakup in a T-Junction 48 'URSOHW%UHDNXSLQD7-XQFWLRQ 3UHYLHZ • LevelSetandPhaseField Ͳ Basefluid:fluid1,Settingfluid:fluid2 • Wettedwall Ͳ Levelset:Dynamiccontactangle(staticcontactangle+sliplength) Ͳ Phasefield:Staticcontactangle Ͳ Movingwettedwall:Onlyphasefield. 49 3UHYLHZ • Fluid1˕ Fluid2ট̛ ࠒࠇ ۶ࢽ – InitialValues,Initialinterface 0RGHO Inlet2 Fluid2 Inlet1 Fluid1 Outlet 50 3K\VLFV LaminarTwoͲPhaseFlow,LevelSet Momentumtransportequation Levelsetequation Densityandviscosity Effectivedropletdiameter 0RGHOLQJ FRQGLWLRQ Fluid2 Symmetry Fluid1 Inlet1 Inlet2 0.4eͲ6/3600*step1(t[1/s])[m^3/s] 0.2eͲ6/3600*step1(t[1/s])[m^3/s] Outlet Pressure,noviscousstress Wall condition Wettedwall Surfacetensioncoefficient 5eͲ3[N/m] 51 5HVXOW 52 Solved with COMSOL Multiphysics 5.0 D r o ple t Br e a k up i n a T- Ju n ct i on Introduction Emulsions consist of small liquid droplets immersed in another liquid, typically oil in water or water in oil. Emulsions find wide application in the production of food, cosmetics, and pharmaceutical products. The properties and quality of an emulsion typically depend on the size and the distribution of the droplets. This model studies in detail how to create uniform droplets in a microchannel T-junction. Setting up the model you can make use of the Laminar Two-Phase Flow, Level Set interface. The model uses the predefined wetted wall boundary condition at the solid walls, with a contact angle of 135°. From the results, you can determine the size of the created droplets and the rate with which they are produced. Model Definition Figure 1 shows the geometry of the T-shaped microchannel with a rectangular cross section. For the separated fluid elements to correspond to droplets, the geometry is modeled in 3D. Due to symmetry, it is sufficient to model only half of the junction geometry. The modeling domain is shown in Figure 1. The fluid to be dispersed into 1 | 53 D R O P L E T B R E A K U P I N A T- J U N C T I O N Solved with COMSOL Multiphysics 5.0 small droplets, Fluid 2, enters through the vertical channel. The other fluid, Fluid 1, flows from the right to left through the horizontal channel. Inlet, fluid 2 Initial fluid interface Inlet, fluid 1 Outlet Figure 1: The modeling domain of the T-junction. The problem described is straight forward to set up with the Laminar Two-Phase Flow, Level Set interface. The interface sets up a momentum transport equation, a continuity equation, and a level set equation for the level set variable. The fluid interface is defined by the 0.5 contour of the level set function. The interface uses the following equations: ρ ∂u T + ρ ( u ⋅ ∇ )u = ∇ ⋅ [ – p I + μ ( ∇u + ( ∇u ) ) ] + F st ∂t ∇⋅u = 0 ∂φ ∇φ------ + u ⋅ ∇φ = γ∇ ⋅ § – φ ( 1 – φ ) --------+ ε∇φ· © ¹ ∂t ∇φ In the equations above, ρ denotes density (kg/m3), u velocity (m/s), t time (s), μ dynamic viscosity (Pa·s), p pressure (Pa), and Fst the surface tension force (N/m3). Furthermore, φ is the level set function, and γ and ε are numerical stabilization parameters. The density and viscosity are calculated from 2 | D R O P L E T B R E A K U P I N A T- J U N C T I O N 54 Solved with COMSOL Multiphysics 5.0 ρ = ρ 1 + ( ρ 2 – ρ 1 )φ μ = μ 1 + ( μ 2 – μ 1 )φ where ρ1, ρ2, μ1, and μ2 are the densities and viscosities of Fluid 1 and Fluid 2. PHYSICAL PARAMETERS The two liquids have the following physical properties: QUANTITY VALUE, FLUID 1 VALUE, FLUID 2 Density (kg/m3) 1000 1000 Dynamic viscosity (Pa·s) 0.00195 0.00671 The surface tension coefficient is 5·10−3 N/m. BOUNDARY CONDITIONS At both inlets, Laminar inflow conditions with prescribed volume flows are used. At the outflow boundary, the Pressure, no viscous stress condition is set. The Wetted wall boundary condition applies to all solid boundaries with the contact angle specified as 135° and a slip length equal to the mesh size parameter, h. The contact angle is the angle between the fluid interface and the solid wall at points where the fluid interface attaches to the wall. The slip length is the distance to the position outside the wall where the extrapolated tangential velocity component is zero (see Figure 2). Fluid 1 u Wall Wall θ Fluid 2 β Figure 2: The contact angle, θ, and the slip length, β. 3 | 55 D R O P L E T B R E A K U P I N A T- J U N C T I O N Solved with COMSOL Multiphysics 5.0 Results and Discussion Figure 3 shows the fluid interface (the level set function φ = 0.5 ) and velocity streamlines at various times. The first droplet is formed after approximately 0.03 s. Figure 3: Velocity streamlines, velocity on the symmetry plane, and the phase boundary at t = 0.02 s, 0.04 s, 0.06 s, and 0.08 s. You can calculate the effective diameter, deff—that is, the diameter of a spherical droplet with the same volume as the formed droplet—using the following expression: 3 d eff = 2 ⋅ 3 -----4π ³Ω ( φ > 0.5 ) dΩ (1) Here, Ω represents the leftmost part of the horizontal channel, where x < −0.2 mm. In this case, the results show that deff is about 0.12 mm. The results are in fair agreement with those presented in Ref. 1. Reference 1. S. van der Graaf, et al., “Lattice Boltzmann Simulations of Droplet Formation in a T-Shaped Microchannel,” Langmuir, vol. 22, pp. 4144–4152, 2006. 4 | D R O P L E T B R E A K U P I N A T- J U N C T I O N 56 Solved with COMSOL Multiphysics 5.0 Model Library path: Microfluidics_Module/Two-Phase_Flow/ droplet_breakup Modeling Instructions From the File menu, choose New. NEW 1 In the New window, click Model Wizard. MODEL WIZARD 1 In the Model Wizard window, click 3D. 2 In the Select physics tree, select Fluid Flow>Multiphase Flow>Two-Phase Flow, Level Set>Laminar Two-Phase Flow, Level Set (tpf). 3 Click Add. 4 Click Study. 5 In the Select study tree, select Preset Studies>Transient with Phase Initialization. 6 Click Done. GEOMETRY 1 1 In the Model Builder window, under Component 1 (comp1) click Geometry 1. 2 In the Settings window for Geometry, locate the Units section. 3 From the Length unit list, choose mm. Work Plane 1 (wp1) 1 On the Geometry toolbar, click Work Plane. 2 In the Settings window for Work Plane, locate the Plane Definition section. 3 From the Plane list, choose xz-plane. Rectangle 1 (r1) 1 On the Work plane toolbar, click Primitives and choose Rectangle. 2 In the Settings window for Rectangle, locate the Size section. 3 In the Width text field, type 0.1. 4 In the Height text field, type 0.4. 5 | 57 D R O P L E T B R E A K U P I N A T- J U N C T I O N Solved with COMSOL Multiphysics 5.0 5 Locate the Position section. In the yw text field, type 0.1. Rectangle 2 (r2) 1 On the Work plane toolbar, click Primitives and choose Rectangle. 2 In the Settings window for Rectangle, locate the Size section. 3 In the Width text field, type 1. 4 In the Height text field, type 0.1. 5 Locate the Position section. In the xw text field, type -0.7. Plane Geometry 1 On the Work plane toolbar, click Build All. 2 Click the Zoom Extents button on the Graphics toolbar. Polygon 1 (pol1) 1 On the Work plane toolbar, click Primitives and choose Polygon. 2 In the Settings window for Polygon, locate the Object Type section. 3 From the Type list, choose Open curve. 4 Locate the Coordinates section. In the xw text field, type 0 0.1. 5 In the yw text field, type 0.2 0.2. 6 Click the Build Selected button. Polygon 2 (pol2) 1 On the Work plane toolbar, click Primitives and choose Polygon. 2 In the Settings window for Polygon, locate the Coordinates section. 3 In the xw text field, type 0.1 0.1. 4 In the yw text field, type 0 0.1. 5 Click the Build Selected button. Extrude 1 (ext1) 1 On the Geometry toolbar, click Extrude. 2 In the Settings window for Extrude, locate the Distances from Plane section. 3 In the table, enter the following settings: Distances (mm) 0.05 4 Click the Build Selected button. 6 | D R O P L E T B R E A K U P I N A T- J U N C T I O N 58 Solved with COMSOL Multiphysics 5.0 5 Click the Zoom Extents button on the Graphics toolbar. Form Union (fin) 1 In the Model Builder window, under Component 1 (comp1)>Geometry 1 right-click Form Union (fin) and choose Build Selected. The geometry should look like in Figure 1. MATERIALS Material 1 (mat1) 1 In the Model Builder window, under Component 1 (comp1) right-click Materials and choose Blank Material. 2 Right-click Material 1 (mat1) and choose Rename. 3 In the Rename Material dialog box, type Fluid 1 in the New label text field. 4 Click OK. 5 In the Settings window for Material, locate the Material Contents section. 6 In the table, enter the following settings: Property Name Value Unit Property group Density rho 1e3[kg /m^3] kg/m³ Basic Dynamic viscosity mu 1.95e3[Pa*s ] Pa·s Basic Material 2 (mat2) 1 In the Model Builder window, right-click Materials and choose Blank Material. 2 Right-click Material 2 (mat2) and choose Rename. 3 In the Rename Material dialog box, type Fluid 2 in the New label text field. 4 Click OK. 5 In the Settings window for Material, click to expand the Material properties section. 6 Locate the Material Properties section. In the Material properties tree, select Basic Properties>Density. 7 Click Add to Material. 8 In the Material properties tree, select Basic Properties>Dynamic Viscosity. 9 Click Add to Material. 7 | 59 D R O P L E T B R E A K U P I N A T- J U N C T I O N Solved with COMSOL Multiphysics 5.0 10 Locate the Material Contents section. In the table, enter the following settings: Property Name Value Unit Property group Density rho 1e3[kg /m^3] kg/m³ Basic Dynamic viscosity mu 6.71e3[Pa*s ] Pa·s Basic DEFINITIONS Step 1 (step1) 1 On the Model toolbar, click Functions and choose Local>Step. 2 In the Settings window for Step, locate the Parameters section. 3 In the Location text field, type 1e-3. 4 Click to expand the Smoothing section. In the Size of transition zone text field, type 2e-3. Add an integration operator that you will use to calculate the effective droplet diameter according to Equation 1 in the Model Definition section. Integration 1 (intop1) 1 On the Definitions toolbar, click Component Couplings and choose Integration. 2 In the Settings window for Integration, locate the Source Selection section. 3 From the Selection list, choose All domains. Variables 1 1 On the Definitions toolbar, click Local Variables. 2 In the Settings window for Variables, locate the Variables section. 3 In the table, enter the following settings: 8 | Name Expression Unit Description V1 0.4e-6/ 3600*step1(t[1/ s])[m^3/s] m³/s Volume flow, inlet 1 V2 0.2e-6/ 3600*step1(t[1/ s])[m^3/s] m³/s Volume flow, inlet 2 d_eff 2*(intop1((phils>0. 5)*(x<-0.2[mm]))*3/ (4*pi))^(1/3) m Effective droplet diameter D R O P L E T B R E A K U P I N A T- J U N C T I O N 60 Solved with COMSOL Multiphysics 5.0 L A M I N A R TW O - P H A S E F L O W, L E V E L S E T ( T P F ) The mesh can be controlled very well in this model, which makes it possible to use a lower element order without reducing the accuracy. 1 In the Model Builder window’s toolbar, click the Show button and select Discretization in the menu. 2 In the Model Builder window, expand the Component 1 (comp1)>Laminar Two-Phase Flow, Level Set (tpf) node, then click Laminar Two-Phase Flow, Level Set (tpf). 3 In the Settings window for Laminar Two-Phase Flow, Level Set, click to expand the Discretization section. 4 From the Discretization of fluids list, choose P1 + P1. Fluid Properties 1 1 In the Model Builder window, under Component 1 (comp1)>Laminar Two-Phase Flow, Level Set (tpf) click Fluid Properties 1. 2 In the Settings window for Fluid Properties, locate the Fluid 1 Properties section. 3 From the Fluid 1 list, choose Fluid 1 (mat1). 4 Locate the Fluid 2 Properties section. From the Fluid 2 list, choose Fluid 2 (mat2). 5 Locate the Surface Tension section. From the Surface tension coefficient list, choose User defined. In the σ text field, type 5e-3[N/m]. 6 Locate the Level Set Parameters section. In the γ text field, type 0.05[m/s]. 7 In the εls text field, type 5e-6[m]. Wall 1 Because this is the default boundary condition node, you cannot modify the selection explicitly. Instead, you override the default condition where it is not applicable by adding other boundary conditions. 1 In the Model Builder window, under Component 1 (comp1)>Laminar Two-Phase Flow, Level Set (tpf) click Wall 1. 2 In the Settings window for Wall, locate the Boundary Condition section. 3 From the Boundary condition list, choose Wetted wall. 4 In the θw text field, type 3*pi/4[rad]. 5 In the β text field, type 5e-6[m]. Initial Interface 1 1 In the Model Builder window, under Component 1 (comp1)>Laminar Two-Phase Flow, Level Set (tpf) click Initial Interface 1. 9 | 61 D R O P L E T B R E A K U P I N A T- J U N C T I O N Solved with COMSOL Multiphysics 5.0 2 Select Boundary 11 only. Initial Values 2 1 On the Physics toolbar, click Domains and choose Initial Values. 2 Select Domain 3 only. 3 In the Settings window for Initial Values, locate the Initial Values section. 4 Click the Fluid 2 button. For Domains 1 and 2, the default initial value settings apply. Inlet 1 1 On the Physics toolbar, click Boundaries and choose Inlet. 2 Select Boundary 22 only. 3 In the Settings window for Inlet, locate the Boundary Condition section. 4 From the list, choose Laminar inflow. 5 Locate the Laminar Inflow section. Click the Flow rate button. 6 In the V0 text field, type V1. 7 In the Lentr text field, type 0.01[m]. Inlet 2 1 On the Physics toolbar, click Boundaries and choose Inlet. 2 Select Boundary 12 only. 3 In the Settings window for Inlet, locate the Level Set Condition section. 4 In the Vf text field, type 1. 5 Locate the Boundary Condition section. From the list, choose Laminar inflow. 6 Locate the Laminar Inflow section. Click the Flow rate button. 7 In the V0 text field, type V2. 8 In the Lentr text field, type 0.01[m]. Outlet 1 1 On the Physics toolbar, click Boundaries and choose Outlet. 2 Select Boundary 1 only. Symmetry 1 1 On the Physics toolbar, click Boundaries and choose Symmetry. 2 Select Boundaries 5, 13, 14, and 21 only. 10 | D R O P L E T B R E A K U P I N A T- J U N C T I O N 62 Solved with COMSOL Multiphysics 5.0 MESH 1 Mapped 1 1 In the Model Builder window, under Component 1 (comp1) right-click Mesh 1 and choose More Operations>Mapped. 2 Select Boundaries 2, 7, 10, and 16 only. Distribution 1 1 Right-click Component 1 (comp1)>Mesh 1>Mapped 1 and choose Distribution. 2 Select Edge 3 only. 3 In the Settings window for Distribution, locate the Distribution section. 4 In the Number of elements text field, type 160. Distribution 2 1 Right-click Mapped 1 and choose Distribution. 2 Select Edges 1 and 9 only. 3 In the Settings window for Distribution, locate the Distribution section. 4 In the Number of elements text field, type 20. Distribution 3 1 Right-click Mapped 1 and choose Distribution. 2 Select Edges 12 and 28 only. 3 In the Settings window for Distribution, locate the Distribution section. 4 From the Distribution properties list, choose Predefined distribution type. 5 In the Number of elements text field, type 25. 6 In the Element ratio text field, type 4. Distribution 4 1 Right-click Mapped 1 and choose Distribution. 2 Select Edges 24 and 27 only. 3 In the Settings window for Distribution, locate the Distribution section. 4 From the Distribution properties list, choose Predefined distribution type. 5 In the Number of elements text field, type 20. 6 In the Element ratio text field, type 3. 7 Select the Reverse direction check box. 11 | 63 D R O P L E T B R E A K U P I N A T- J U N C T I O N Solved with COMSOL Multiphysics 5.0 Mapped 1 Right-click Mapped 1 and choose Build Selected. Swept 1 1 Right-click Mesh 1 and choose Swept. 2 In the Settings window for Swept, click to expand the Source faces section. 3 Locate the Source Faces section. Select the Active toggle button. 4 Select Boundaries 2, 7, and 10 only. Distribution 1 1 Right-click Component 1 (comp1)>Mesh 1>Swept 1 and choose Distribution. 2 In the Settings window for Distribution, locate the Distribution section. 3 In the Number of elements text field, type 10. 4 Click the Build All button. STUDY 1 Step 2: Time Dependent 1 In the Model Builder window, expand the Study 1 node, then click Step 2: Time Dependent. 2 In the Settings window for Time Dependent, locate the Study Settings section. 3 In the Times text field, type range(0,5e-3,0.08). 12 | D R O P L E T B R E A K U P I N A T- J U N C T I O N 64 Solved with COMSOL Multiphysics 5.0 4 Click to expand the Results while solving section. Locate the Results While Solving section. Select the Plot check box. 5 From the Plot group list, choose Default. This choice means that the Graphics window will show a surface plot of the volume fraction of Fluid 1 while solving, and this plot will be updated at each 5 ms output time step. Manually tune the solver sequence for optimal performance and accuracy. Solution 1 1 On the Study toolbar, click Show Default Solver. 2 In the Model Builder window, expand the Solution 1 node, then click Time-Dependent Solver 1. 3 In the Settings window for Time-Dependent Solver, click to expand the Time stepping section. 4 Locate the Time Stepping section. From the Method list, choose Generalized alpha. 5 Select the Time step increase delay check box. 6 In the associated text field, type 3. 7 In the Amplification for high frequency text field, type 0.3. 8 From the Predictor list, choose Constant. 9 In the Model Builder window, expand the Study 1>Solver Configurations>Solution 1>Time-Dependent Solver 1 node. 10 Right-click Study 1>Solver Configurations>Solution 1>Time-Dependent Solver 1 and choose Iterative. 11 In the Settings window for Iterative, locate the Error section. 12 In the Factor in error estimate text field, type 20. 13 In the Maximum number of iterations text field, type 200. 14 Right-click Study 1>Solver Configurations>Solution 1>Time-Dependent Solver 1>Iterative 1 and choose Multigrid. 15 In the Model Builder window, expand the Study 1>Solver Configurations>Solution 1>Time-Dependent Solver 1>Iterative 1>Multigrid 1 node. 16 Right-click Presmoother and choose SCGS. 17 In the Settings window for SCGS, locate the Main section. 18 Select the Vanka check box. 13 | 65 D R O P L E T B R E A K U P I N A T- J U N C T I O N Solved with COMSOL Multiphysics 5.0 19 Under Variables, click Add. 20 In the Add dialog box, In the Variables list, choose comp1.tpf.Pinlinl1 and comp1.tpf.Pinlinl2. 21 Click OK. 22 In the Model Builder window, expand the Study 1>Solver Configurations>Solution 1>Time-Dependent Solver 1>Iterative 1>Multigrid 1>Postsmoother node. 23 Right-click Study 1>Solver Configurations>Solution 1>Time-Dependent Solver 1>Iterative 1>Multigrid 1>Postsmoother and choose SCGS. 24 In the Settings window for SCGS, locate the Main section. 25 Select the Vanka check box. 26 Under Variables, click Add. 27 In the Add dialog box, In the Variables list, choose comp1.tpf.Pinlinl1 and comp1.tpf.Pinlinl2. 28 Click OK. 29 In the Model Builder window, expand the Study 1>Solver Configurations>Solution 1>Time-Dependent Solver 1>Iterative 1>Multigrid 1>Coarse Solver node, then click Direct. 30 In the Settings window for Direct, locate the General section. 31 From the Solver list, choose PARDISO. 32 In the Model Builder window, collapse the Study 1>Solver Configurations>Solution 1>Time-Dependent Solver 1 node. STUDY 1 Solution 1 1 In the Model Builder window, collapse the Study 1>Solver Configurations>Solution 1>Time-Dependent Solver 1 node. 2 In the Model Builder window, collapse the Solution 1 node. 3 On the Study toolbar, click Compute. RESULTS The first default plot group shows the volume fraction of fluid 1 as slice plot, and the second plot group shows a slice plot of the velocity combined with a contour plot of the volume fraction of fluid 1. Follow these steps to reproduce the series of velocity field plots shown in Figure 3. 14 | D R O P L E T B R E A K U P I N A T- J U N C T I O N 66 Solved with COMSOL Multiphysics 5.0 3D Plot Group 3 1 On the Model toolbar, click Add Plot Group and choose 3D Plot Group. 2 In the Model Builder window, under Results right-click 3D Plot Group 3 and choose Slice. 3 In the Settings window for Slice, click Replace Expression in the upper-right corner of the Expression section. From the menu, choose Component 1>Laminar Two-Phase Flow, Level Set>tpf.U - Velocity magnitude. 4 Locate the Plane Data section. From the Plane list, choose zx-planes. 5 From the Entry method list, choose Coordinates. 6 On the 3D plot group toolbar, click Plot. 7 In the Model Builder window, right-click 3D Plot Group 3 and choose Isosurface. 8 In the Settings window for Isosurface, locate the Levels section. 9 From the Entry method list, choose Levels. 10 In the Levels text field, type 0.5. 11 Locate the Coloring and Style section. From the Coloring list, choose Uniform. 12 From the Color list, choose Green. 13 Right-click 3D Plot Group 3 and choose Streamline. 14 In the Settings window for Streamline, locate the Streamline Positioning section. 15 From the Positioning list, choose Uniform density. 16 In the Separating distance text field, type 0.05. 17 Locate the Coloring and Style section. From the Line type list, choose Tube. 18 Select the Radius scale factor check box. 19 In the associated text field, type 2e-3. 20 From the Color list, choose Yellow. 21 In the Model Builder window, click 3D Plot Group 3. 22 In the Settings window for 3D Plot Group, locate the Data section. 23 From the Time (s) list, choose 0.02000. 24 On the 3D plot group toolbar, click Plot. 25 Click the Go to Default 3D View button on the Graphics toolbar. Compare the resulting plot with the upper-left plot in Figure 3. 26 To reproduce the remaining three plots, plot the solution for the time values 0.04, 0.06, and 0.08 s. 15 | 67 D R O P L E T B R E A K U P I N A T- J U N C T I O N Solved with COMSOL Multiphysics 5.0 Next, evaluate the effective droplet diameter computed according to Equation 1. Derived Values 1 On the Results toolbar, click Global Evaluation. 2 In the Settings window for Global Evaluation, click Replace Expression in the upper-right corner of the Expression section. From the menu, choose Component 1>Definitions>Variables>d_eff - Effective droplet diameter. 3 Click the Evaluate button. TABLE 1 Go to the Table window. The result, roughly 0.12 mm, is displayed in the table in the Table window. Finally, generate a movie of the moving fluid interface and the velocity streamlines. RESULTS Export 1 In the Model Builder window, under Results right-click 3D Plot Group 3 and choose Player. COMSOL Multiphysics generates the movie and then plays it. 2 To replay the movie, click the Play button on the Graphics toolbar. If you want to export a movie in GIF, Flash, or AVI format, right-click Export and create an Animation feature. 16 | D R O P L E T B R E A K U P I N A T- J U N C T I O N 68 Cooling of an Injection Mold 69 CoolingofanInjectionMold 3UHYLHZ • Simulationsoffluidflow,heatandmasstransfer,hydraulictransients,andacousticsinthe1Dgeometry. • FluidModel– Newtonian,Powerlaw,Bingham • Pipeshape– Round,Square,Rectangle,Userdefined(hydraulicdiameter) • Inlet/Outlet– Massflowrate,Velocity,Volumetricflowrate,SCCM 70 3UHYLHZ • Frictionmodel Ͳ Newtonianfluids Churchill:FullrangeofRe(laminar,transitionandturbulent)ande/d Stokes:Laminarregime(Re<2000) Wood:4*103 <Re<1*107 and1*10Ͳ5 <e/d<4*10Ͳ2 Haaland :Commonlyusedforoilpipelinesandwells,Re(4*103 <Re<1*108) Colebrook:Verylowrelativeroughnesse/d,SimpleHaaland model VonKarman:Verylargerelativeroughnesse/d,SimpleHaaland model SwameeͲJain:AlternativemethodofHaaland model 10Ͳ6 <e/d<10Ͳ2 andforRe(5*103 <Re<108) Ͳ NonͲNewtonianfluids Irvine(Powerlaw):FullrangeofRe(laminar,transitionandturbulent)ande/d Stokes(Powerlaw):Laminarregime(Re<2000) Darby(Bingham):FullrangeofRe(laminar,transitionandturbulent)ande/d 3UHYLHZ • LossCoefficients 71 3UHYLHZ • WallHeatTransfer 0RGHO Steel AISI4340 Polyurethane Thermalconductivity 44.5[W/(m*K)] 0.32[W/(m*K)] Density 7850[kg/ี@ 1250[kg/ี@ Heatcapacity 475[J/(kg*K)] 1540[J/(kg*K)] 72 3K\VLFV PipeFlow+HeatTransferinPipes=NonͲIsothermalPipeFlow + HeatTransferinSolid ContinuityandMomentumEquations ChurchillModel EnergyEquation 0RGHOLQJ FRQGLWLRQ Pipediameter:1cm Inlet 10[Liter/min] Outlet 1[atm] Initialtemperatureof mold 473.15K Surfaceroughness Commercialsteel(0.046mm) 73 5HVXOW MoldMaterial Waterflowrate Surface averageTafter (l/min) roughness(mm) 10min(K) Linecolor Steel 10 0.046 333 Blue Steel 20 0.046 325 Green Steel 10 0.46 328 Red Aluminium 10 0.046 301 Magenta 74 Solved with COMSOL Multiphysics 5.0 Cooling of an Injection Mold Introduction Cooling is an important process in the production of injection molded plastics. First of all, the cooling time may well represent more than half of the production cycle time. Second, a homogeneous cooling process is desired to avoid defects in the manufactured parts. If plastic materials in the injection molding die are cooled down uniformly and slowly, residual stresses can be avoided, and thereby the risk of warps and cracks in the end product can be minimized. As a consequence, the positioning and properties of the cooling channels become important aspects when designing the mold. The simulation of heat transfer in molds of relatively complex geometries requires a 3D representation. Simulation of 3D flow and heat transfer inside the cooling channels are computationally expensive. An efficient short-cut alternative is to model the flow and heat transfer in the cooling channels with 1D pipe flow equations, and still model the surrounding mold and product in 3D. This example shows how you can use the Non-Isothermal Pipe Flow interface together with the Heat Transfer in Solids interface to model a mold cooling process. The equations describing the cooling channels are fully coupled to the heat transfer equations of the mold and the polyurethane part. Figure 1: The steering wheel of a car, made from polyurethane. 1 | 75 COOLING OF AN INJECTION MOLD Solved with COMSOL Multiphysics 5.0 Model Definition MODEL GEOMETRY AND PROCESS CONDITIONS The polyurethane material used for a steering wheel is produced by several different molds. The part considered in this model is the top half of the wheel grip, shown in gray in Figure 2. Figure 2: Polyurethane parts for a steering wheel. The top half of the grip is modeled in this example. 2 | COOLING OF AN INJECTION MOLD 76 Solved with COMSOL Multiphysics 5.0 The mold consists of a 50-by-50-by-15 cm steel block. Two cooling channels, 1 cm in diameter, are machined into the block as illustrated in Figure 3. Water inlets Figure 3: Mold block and cooling channels. The after injection of the polyurethane, the average temperature of the mold a the plastic material is 473 K. Water at room temperature is used as cooling fluid and flows through the channels at a rate of 10 liters/min. The model simulates a 10 min cooling process. For numerical stability reasons, the model is set up with an initial water temperature of 473 K, which is ramped down to 288 K during the first few seconds. PIPE FLOW EQUATIONS The momentum and mass conservation equations below describe the flow in the cooling channels: ∂u ρ ρ ------- = – ∇p – f D ---------- u u ∂t 2d h (1) ∂Aρ ----------- + ∇ ⋅ ( Aρu ) = 0 ∂t (2) 3 | 77 COOLING OF AN INJECTION MOLD Solved with COMSOL Multiphysics 5.0 Above, u is the cross section averaged fluid velocity (m/s) along the tangent of the center line of a pipe. A (m2) is the cross section area of the pipe, ρ (kg/m3) is the density, and p (N/m2) is the pressure. For more information, refer to the section Theory for the Pipe Flow Interface in the Pipe Flow Module User’s Guide. Expressions for the Darcy Friction Factor The second term on the right hand side of Equation 2 accounts for pressure drop due to viscous shear. The Pipe Flow physics uses the Churchill friction model (Ref. 1) to calculate fD. It is valid for laminar flow, turbulent flow, and the transitional region in between. The Churchill friction model is predefined in the Non-Isothermal Pipe Flow interface and is given by: 8 12 -1.5 f D = 8 § ------· + ( A + B ) © Re¹ 1 ⁄ 12 (3) where 7 A = -2.457ln § § ------· © © Re¹ 0.9 + 0.27 ( e ⁄ d )· ¹ 37530 16 B = §© ----------------·¹ Re 4 | COOLING OF AN INJECTION MOLD 78 16 (4) (5) Solved with COMSOL Multiphysics 5.0 As seen from the equations above, the friction factor depends on the surface roughness divided by diameter of the pipe, e/d. Surface roughness values can be selected from a list in the Pipe Properties feature or be entered as user-defined values. Figure 4: The Friction model and Surface roughness settings are found in the Pipe Properties feature. In the Churchill equation, fD is also a function of the fluid properties, flow velocity and geometry, through the Reynolds number: ρud Re = ----------μ (6) The physical properties of water as function of temperature are directly available from the software’s built-in material library. H E A T TR A N S F E R E Q U A T I O N S Cooling Channels The energy equation for the cooling water inside the pipe is: ρA ∂T 3 ρAC p ------- + ρAC p u ⋅ ∇T = ∇ ⋅ Ak ∇T + f D ---------- u + Q wall 2d h ∂t (7) where Cp (J/(kg·K)) is the heat capacity at constant pressure, T is the cooling water temperature (K), and k (W/(m·K)) is the thermal conductivity. The second term on the right hand side corresponds to heat dissipated due to internal friction in the fluid. It is negligible for the short channels considered here. Qwall (W/m) is a source term that accounts for the heat exchange with the surrounding mold block. 5 | 79 COOLING OF AN INJECTION MOLD Solved with COMSOL Multiphysics 5.0 Mold Block and Polyurethane Part Heat transfer in the solid steel mold block as well as the molded polyurethane part is governed by conduction: ∂T 2 ρC p ---------- = ∇ ⋅ k ∇T 2 ∂t (8) Above, T2 is the temperature in the solids. The source term Qwall comes into play for the heat balance in Equation 8 through a line heat source where the pipe is situated. This coupling is automatically done by the Wall Heat Transfer feature in the Non-Isothermal Pipe Flow interface. Heat Exchange The heat exchange term Qwall (W/m) couple the two energy balances given by Equation 7 and Equation 8: The heat transfer through the pipe wall is given by Q wall = hZ ( T ext – T ) (9) In Equation 9 Z (m) is the perimeter of the pipe, h (W/(m2·K)) a heat transfer coefficient and Text (K) the external temperature outside of the pipe. Qwall appears as a source term in the pipe heat transfer equation. The Wall heat transfer feature requires the external temperature and at least an internal film resistance. Text can be a constant, parameter, expression, or given by a temperature field computed by another physics interface, typically a 3D Heat Transfer interface. h is automatically calculated through film resistances and wall layers that are added as subnodes. For details, refer to the section Theory for the Heat Transfer in Pipes Interface in the Pipe Flow Module User’s Guide. In this model example, Text is given as the temperature field computed by a 3D heat transfer interface, and automatic heat transfer coupling is done to the 3D physics side as a line source. The temperature coupling between the pipe and the surrounding domain is implemented as a line heat source in the 3D domain. The source strength is proportional to the temperature difference between the pipe fluid and the surrounding domain. 6 | COOLING OF AN INJECTION MOLD 80 Solved with COMSOL Multiphysics 5.0 The Wall Heat Transfer feature is added to the Non-Isothermal Pipe Flow interface, and the External temperature is set to the temperature of the Heat Transfer in solids interface. Figure 5: In the Wall Heat Transfer feature, set the External temperature to the temperature field computed by the Heat Transfer in Solids interface. The heat transfer coefficient, h, depends on the physical properties of water and the nature of the flow and is calculated from the Nusselt number: k h = Nu -----dh (9-6) where k is the thermal conductivity of the material, and Nu is the Nusselt number. dh is the hydraulic diameter of the pipe. COMSOL detects if the flow is laminar or turbulent. For the laminar flow regime, an analytic solution is available that gives Nu = 3.66 for circular tubes (Ref. 2). For turbulent flow inside channels of circular cross sections the following Nusselt correlation is used (Ref. 3): ( f D ⁄ 8 ) ( Re – 1000 )Pr Nu int = -----------------------------------------------------------------------------1⁄2 2⁄3 1 + 12.7 ( f D ⁄ 8 ) ( Pr – 1) (10) where Pr is the Prandtl number: Cp μ Pr = ----------k (11) Note that Equation 10 is a function of the friction factor, fD, and therefore that the radial heat transfer will increase with the surface roughness of the channels. Note: All the correlations discussed above are automatically used by the Wall Heat Transfer feature in the Pipe Flow Module, and it detects if the flow is laminar or turbulent for automatic selection of the correct correlation. 7 | 81 COOLING OF AN INJECTION MOLD Solved with COMSOL Multiphysics 5.0 Results and Discussion The steel mold and polyurethane part, initially at 473 K, are cooled for 10 minutes by water at room temperature. Figures below show sample results when flow rate of the cooling water is 10 liters/minute and the surface roughness of the channels is 46 μm. After two minutes of cooling, the hottest and coldest parts of the polyurethane part differ by approximately 40 K (Figure 7). Figure 7: Temperature distribution in the polyurethane part and the cooling channels after 2 minutes of cooling. 8 | COOLING OF AN INJECTION MOLD 82 Solved with COMSOL Multiphysics 5.0 Figure 8 shows the temperature distribution in the steel mold after 2 minutes. The temperature footprint of the cooling channels is clearly visible. Figure 8: Temperature distribution in the steel mold block after 2 minutes of cooling. 9 | 83 COOLING OF AN INJECTION MOLD Solved with COMSOL Multiphysics 5.0 After 10 minutes of cooling, the temperature in the mold block is more uniform, with a temperature at the center of approximately 333 K (Figure 9). Still, the faces with cooling channel inlets and outlets are more than 20 K hotter. Figure 9: Temperature distribution in the steel mold block after 10 minutes of cooling. The blue line in Figure 10 shows the average temperature of the polyurethane part as function of the cooling time. The temperature is 333 K after 10 minutes of cooling. To evaluate the influence of factors affecting the cooling time, additional simulations can be run, varying the flow rate of the cooling water, the surface roughness of the cooling channels, and the mold material. The conditions are summarized in the table below. TABLE 1: COOLING CONDITIONS 10 | MOLD MATERIAL WATER FLOW RATE (L/MIN) SURFACE ROUGHNESS (MM) AVERAGE T AFTER 10 MIN (K) LINE COLOR Steel 10 0.046 333 Blue Steel 20 0.046 325 Green Steel 10 0.46 328 Red Aluminum 10 0.046 301 Magenta COOLING OF AN INJECTION MOLD 84 Solved with COMSOL Multiphysics 5.0 Figure 10: Average temperature of the polyurethane part as function of time and cooling conditions. Clearly, the thermal conductivity of the mold material is the most important factor in this comparison, followed by flow rate and surface roughness of the cooling channels. Assuming that 340 K is an acceptable temperature at the end of the production cycle, it can be found that changing the mold material reduces the cooling time by 67%, increasing the flow rate reduces the cooling time by 17%, and increasing surface roughness reduces the cooling time by 11%. References 1. S.W. Churchill, “Friction factor equations span all fluid-flow regimes,” Chem. Eng., vol. 84, no. 24, p.91, 1997. 2. F.P. Incropera, D.P. DeWitt. Fundamentals of Heat and Mass Transfer, 5th ed., John Wiley & Sons, pp. 486–487, 2002. 3. V. Gnielinski, “New Equation for Heat and Mass Transfer in Turbulent Pipe and Channel Flow,” Int. Chem. Eng. vol. 16, p. 359, 1976. 11 | 85 COOLING OF AN INJECTION MOLD Solved with COMSOL Multiphysics 5.0 Model Library path: Pipe_Flow_Module/Heat_Transfer/mold_cooling Modeling Instructions From the File menu, choose New. NEW 1 In the New window, click Model Wizard. MODEL WIZARD 1 In the Model Wizard window, click 3D. 2 In the Select physics tree, select Fluid Flow>Non-Isothermal Flow>Non-Isothermal Pipe Flow (nipfl). 3 Click Add. 4 In the Select physics tree, select Heat Transfer>Heat Transfer in Solids (ht). 5 Click Add. 6 Click Study. 7 In the Select study tree, select Preset Studies for Selected Physics Interfaces>Time Dependent. 8 Click Done. DEFINITIONS Parameters 1 On the Model toolbar, click Parameters. 2 In the Settings window for Parameters, locate the Parameters section. 3 In the table, enter the following settings: 12 | Name Expression Value Description T_init_mo ld 473.15[K] 473.15 K Initial temperature, mold T_coolant 288.15[K] 288.15 K Steady-state inlet temperature, coolant COOLING OF AN INJECTION MOLD 86 Solved with COMSOL Multiphysics 5.0 Step 1 (step1) Create a smooth step function to decrease the coolant temperature at the beginning of the process. 1 On the Model toolbar, click Functions and choose Global>Step. 2 In the Settings window for Step, locate the Parameters section. 3 In the Location text field, type 2.5. 4 In the From text field, type 1. 5 In the To text field, type 0. 6 Click to expand the Smoothing section. In the Size of transition zone text field, type 5. Optionally, you can inspect the shape of the step function: 7 Click the Plot button. Variables 1 1 On the Model toolbar, click Variables and choose Global Variables. 2 In the Settings window for Variables, locate the Variables section. 13 | 87 COOLING OF AN INJECTION MOLD Solved with COMSOL Multiphysics 5.0 3 In the table, enter the following settings: Name Expression Unit Description T_inlet T_coolant+(T_init_m old-T_coolant)*step 1(t[1/s]) K Ramped inlet temperature, coolant GEOMETRY 1 First, import the steering wheel part from a CAD design file. Import 1 (imp1) 1 On the Model toolbar, click Import. 2 In the Settings window for Import, locate the Import section. 3 Click Browse. 4 Browse to the model’s Model Library folder and double-click the file mold_cooling_top.mphbin. 5 Click Import. 6 Click the Zoom Extents button on the Graphics toolbar. Second, draw the mold and cooling channels. To simplify this step, insert a prepared geometry sequence from file. After insertion you can study each geometry step in the sequence. 7 On the Geometry toolbar, click Insert Sequence. 8 Browse to the model’s Model Library folder and double-click the file mold_cooling_geom_sequence.mph. Block 1 (blk1) 1 In the Model Builder window, under Component 1 (comp1)>Geometry 1 right-click Block 1 (blk1) and choose Build All Objects. 2 Click the Zoom Extents button on the Graphics toolbar. 3 Click the Transparency button on the Graphics toolbar. DEFINITIONS Create the selections to simplify the model specification. Explicit 1 1 On the Definitions toolbar, click Explicit. 2 In the Settings window for Explicit, locate the Input Entities section. 14 | COOLING OF AN INJECTION MOLD 88 Solved with COMSOL Multiphysics 5.0 3 From the Geometric entity level list, choose Edge. Select one segment of the upper channel and one segment of the lower. 4 Select Edges 6 and 7 only. 5 Select the Group by continuous tangent check box to select entire channels. 6 Right-click Component 1 (comp1)>Definitions>Explicit 1 and choose Rename. 7 In the Rename Explicit dialog box, type Cooling channels in the New label text field. 8 Click OK. MATERIALS The next step is to specify material properties for the model. Select water and steel from the built-in materials database. ADD MATERIAL 1 On the Model toolbar, click Add Material to open the Add Material window. 2 Go to the Add Material window. 3 In the tree, select Built-In>Water, liquid. 4 Click Add to Component in the window toolbar. MATERIALS Water, liquid (mat1) 1 In the Model Builder window, under Component 1 (comp1)>Materials click Water, liquid (mat1). 2 In the Settings window for Material, locate the Geometric Entity Selection section. 15 | 89 COOLING OF AN INJECTION MOLD Solved with COMSOL Multiphysics 5.0 3 From the Geometric entity level list, choose Edge. 4 From the Selection list, choose Cooling channels. ADD MATERIAL 1 Go to the Add Material window. 2 In the tree, select Built-In>Steel AISI 4340. 3 Click Add to Component in the window toolbar. 4 On the Model toolbar, click Add Material to close the Add Material window. MATERIALS Steel AISI 4340 (mat2) 1 In the Model Builder window, under Component 1 (comp1)>Materials click Steel AISI 4340 (mat2). 2 Select Domain 1 only. Material 3 (mat3) Next, create a material with the properties of polyurethane. 1 In the Model Builder window, right-click Materials and choose Blank Material. 2 Select Domain 2 only. 3 In the Settings window for Material, locate the Material Contents section. 4 In the table, enter the following settings: Property Name Value Unit Property group Thermal conductivity k 0.32 W/ (m·K) Basic Density rho 1250 kg/m³ Basic Heat capacity at constant pressure Cp 1540 J/ (kg·K) Basic 5 Right-click Component 1 (comp1)>Materials>Material 3 (mat3) and choose Rename. 6 In the Rename Material dialog box, type Polyurethane in the New label text field. 7 Click OK. NON-ISOTHERMAL PIPE FLOW (NIPFL) 1 In the Settings window for Non-Isothermal Pipe Flow, locate the Edge Selection section. 16 | COOLING OF AN INJECTION MOLD 90 Solved with COMSOL Multiphysics 5.0 2 From the Selection list, choose Cooling channels. Pipe Properties 1 1 In the Model Builder window, under Component 1 (comp1)>Non-Isothermal Pipe Flow (nipfl) click Pipe Properties 1. 2 In the Settings window for Pipe Properties, locate the Pipe Shape section. 3 From the list, choose Round. 4 In the di text field, type 1[cm]. 5 Locate the Flow Resistance section. From the Surface roughness list, choose Commercial steel (0.046 mm). Temperature 1 1 In the Model Builder window, under Component 1 (comp1)>Non-Isothermal Pipe Flow (nipfl) click Temperature 1. 2 In the Settings window for Temperature, locate the Temperature section. 3 In the Tin text field, type T_inlet. Inlet 1 1 On the Physics toolbar, click Points and choose Inlet. 2 Select Points 3 and 4 only. 3 In the Settings window for Inlet, locate the Inlet Specification section. 4 From the Specification list, choose Volumetric flow rate. 5 In the qv,0 text field, type 10[l/min]. Heat Outflow 1 1 On the Physics toolbar, click Points and choose Heat Outflow. 2 Select Points 269 and 270 only. Wall Heat Transfer 1 1 On the Physics toolbar, click Edges and choose Wall Heat Transfer. 2 In the Settings window for Wall Heat Transfer, locate the Edge Selection section. 3 From the Selection list, choose Cooling channels. 4 Locate the Heat Transfer Model section. From the Text list, choose Temperature (ht). Initial Values 1 1 Right-click Component 1 (comp1)>Non-Isothermal Pipe Flow (nipfl)>Wall Heat Transfer 1 and choose Internal Film Resistance. 2 In the Settings window for Initial Values, locate the Initial Values section. 17 | 91 COOLING OF AN INJECTION MOLD Solved with COMSOL Multiphysics 5.0 3 In the u text field, type 0.1. 4 In the T text field, type T_init_mold. H E A T TR A N S F E R I N S O L I D S ( H T ) 1 In the Model Builder window, expand the Component 1 (comp1)>Heat Transfer in Solids (ht) node, then click Initial Values 1. 2 In the Settings window for Initial Values, locate the Initial Values section. 3 In the T2 text field, type T_init_mold. Heat Flux 1 1 On the Physics toolbar, click Boundaries and choose Heat Flux. 2 In the Settings window for Heat Flux, locate the Boundary Selection section. 3 From the Selection list, choose All boundaries. 4 Locate the Heat Flux section. Click the Convective heat flux button. 5 In the h text field, type 2. MESH 1 Edge 1 1 In the Model Builder window, under Component 1 (comp1) right-click Mesh 1 and choose More Operations>Edge. 2 In the Settings window for Edge, locate the Edge Selection section. 3 From the Selection list, choose Cooling channels. Size 1 1 Right-click Component 1 (comp1)>Mesh 1>Edge 1 and choose Size. 2 In the Settings window for Size, locate the Element Size section. 3 From the Predefined list, choose Extra fine. 4 In the Model Builder window, right-click Mesh 1 and choose Free Tetrahedral. Size 1 In the Model Builder window, under Component 1 (comp1)>Mesh 1 click Size. 2 In the Settings window for Size, locate the Element Size section. 3 Click the Custom button. 4 Locate the Element Size Parameters section. In the Minimum element size text field, type 0.003. 5 In the Model Builder window, right-click Mesh 1 and choose Build All. 18 | COOLING OF AN INJECTION MOLD 92 Solved with COMSOL Multiphysics 5.0 STUDY 1 Step 1: Time Dependent 1 In the Model Builder window, expand the Study 1 node, then click Step 1: Time Dependent. 2 In the Settings window for Time Dependent, locate the Study Settings section. 3 In the Times text field, type range(0,30,600). 4 On the Model toolbar, click Compute. RESULTS Data Sets 1 On the Results toolbar, click More Data Sets and choose Solution. 2 On the Results toolbar, click Selection. 3 In the Settings window for Selection, locate the Geometric Entity Selection section. 4 From the Geometric entity level list, choose Domain. 5 Select Domain 2 only. 6 On the Results toolbar, click More Data Sets and choose Solution. 7 On the Results toolbar, click Selection. 8 In the Settings window for Selection, locate the Geometric Entity Selection section. 9 From the Geometric entity level list, choose Boundary. 10 Select Boundaries 3 and 5 only. Temperature (nipfl) 1 In the Model Builder window, expand the Results>Temperature (nipfl) node, then click Line 1.1. 2 In the Settings window for Line, locate the Coloring and Style section. 3 Select the Radius scale factor check box. 4 In the associated text field, type 1. 5 Clear the Color legend check box. 6 Locate the Data section. From the Data set list, choose Study 1/Solution 1 (1). 7 From the Time (s) list, choose 120.00. 8 In the Model Builder window, right-click Temperature (nipfl) and choose Surface. 9 In the Settings window for Surface, locate the Data section. 10 From the Data set list, choose Study 1/Solution 1 (2). 19 | 93 COOLING OF AN INJECTION MOLD Solved with COMSOL Multiphysics 5.0 11 From the Time (s) list, choose 120.00. 12 Click Replace Expression in the upper-right corner of the Expression section. From the menu, choose Model>Component 1>Heat Transfer in Solids>Temperature>T2 Temperature. 13 On the 3D plot group toolbar, click Plot. 14 Click the Zoom Extents button on the Graphics toolbar. Temperature (ht) 1 In the Model Builder window, under Results click Temperature (ht). 2 In the Settings window for 3D Plot Group, locate the Data section. 3 From the Time (s) list, choose 120.00. 4 On the 3D plot group toolbar, click Plot. 5 Click the Transparency button on the Graphics toolbar. 6 In the Model Builder window, expand the Temperature (ht) node, then click Surface 1. 7 In the Settings window for Surface, locate the Coloring and Style section. 8 From the Color table list, choose Rainbow. 9 On the 3D plot group toolbar, click Plot. 3D Plot Group 6 1 On the Model toolbar, click Add Plot Group and choose 3D Plot Group. 2 In the Model Builder window, under Results right-click 3D Plot Group 6 and choose Surface. 3 In the Settings window for Surface, locate the Data section. 4 From the Data set list, choose Study 1/Solution 1 (3). 5 Click Replace Expression in the upper-right corner of the Expression section. From the menu, choose Model>Component 1>Heat Transfer in Solids>Temperature>T2 Temperature. 6 In the Model Builder window, right-click 3D Plot Group 6 and choose Slice. 7 In the Settings window for Slice, locate the Plane Data section. 8 In the Planes text field, type 4. 9 Click to expand the Inherit style section. Locate the Inherit Style section. From the Plot list, choose Surface 1. 10 Click Replace Expression in the upper-right corner of the Expression section. From the menu, choose Model>Component 1>Heat Transfer in Solids>Temperature>T2 Temperature. 20 | COOLING OF AN INJECTION MOLD 94 Solved with COMSOL Multiphysics 5.0 11 Right-click 3D Plot Group 6 and choose Surface. 12 In the Settings window for Surface, locate the Data section. 13 From the Data set list, choose Study 1/Solution 1 (2). 14 Locate the Expression section. In the Expression text field, type 0. 15 Locate the Coloring and Style section. From the Coloring list, choose Uniform. 16 From the Color list, choose Gray. 17 Right-click 3D Plot Group 6 and choose Line. 18 In the Settings window for Line, click Replace Expression in the upper-right corner of the Expression section. From the menu, choose Model>Component 1>Non-Isothermal Pipe Flow (Heat Transfer in Pipes)>T - Temperature. 19 Locate the Coloring and Style section. From the Line type list, choose Tube. 20 In the Tube radius expression text field, type 0.5*nipfl.dh. 21 Select the Radius scale factor check box. 22 From the Coloring list, choose Uniform. 23 From the Color list, choose Blue. 24 On the 3D plot group toolbar, click Plot. Derived Values 1 On the Results toolbar, click More Derived Values and choose Average>Volume Average. 2 In the Settings window for Volume Average, locate the Selection section. 3 Click Paste Selection. 4 In the Paste Selection dialog box, type 2 in the Selection text field. 5 Click OK. 6 In the Settings window for Volume Average, click Replace Expression in the upper-right corner of the Expression section. From the menu, choose Model>Component 1>Heat Transfer in Solids>Temperature>T2 - Temperature. 7 Click the Evaluate button. 21 | 95 COOLING OF AN INJECTION MOLD Solved with COMSOL Multiphysics 5.0 22 | COOLING OF AN INJECTION MOLD 96 Electroosmotic Micromixer 97 (OHFWURRVPRWLF 0LFURPL[HU 3UHYLHZ • Particlerelease(Inlet,Release)– Meshbased(refine^dimension) Refinementfactor=1 Refinementfactor=3 98 3UHYLHZ • Particlerelease(Inlet,Release)– Density Theresultingdistributionwilllookabitrandom,anditwilldependontheorderin whichthemeshelementsarenumbered. Expression=x+y2 Expression=1 3UHYLHZ • Particlerelease– Grid(Releaseofgrid),uniformdensity(inlet) Releaseuniformlyfrom0.3to0.7 Uniformreleaseonaboundary 99 3UHYLHZ • Bounce Ͳ Thisoptionspecularly reflectsfromthewallsuchthattheparticlemomentumisconserved. Ͳ ThisoptionisnotavailableforMassless particletracing Ͳ Thisoptionistypicallyusedwhentracingmicroscopicparticlesinafluid. • Freeze Ͳ Thisoption(default)fixestheparticlepositionandvelocityattheinstantawallisstruck. Ͳ Thisisusefultorecoverthevelocityandenergydistributionfunctionofparticleswhentheystrikethewall Ͳ Usedtocomputetheionenergydistributionfunctioninplasmamodels • Stick Ͳ Thisoptionfixestheparticlepositionattheinstantthewallisstruck. Ͳ Thiscanbeusedifthevelocityorenergyoftheparticlesstrikingawallisnotofinterest. 3UHYLHZ • Disappear Ͳ Thisoptionmeansthattheparticleisnotdisplayedonceithasmadecontactwiththewall. Ͳ Thisoptionshouldbeusedifdisplayoftheparticlelocationaftercontactwiththewallisnotofinterest. •Diffusereflection Ͳ ParticlesbounceoffsurfacesaccordingtoKnudsen’scosinelaw •Generalreflection Ͳ Specifyanarbitraryexpressionforthepostcollisionparticlevelocity Ͳ Intheexampletotherightparticleswillbespecularly reflectedoffawallwithhalfoftheirincidentvelocity Ͳ Thisoptiongivescompletefreedomover 100 0RGHO Mixing Inlet Electroosmotic velocity Outlet Property Density Dynamicviscosity Name rho mu Value 1e3[kg/m^3] 1eͲ3[Pa*s] Electricconductivity sigma 0.11845[S/m] Relativepermittivity epsilonr 80.2 3K\VLFV ElectricCurrents+LaminarFlow+TransportofDilutedSpecies NavierͲstokesequation (Compressibleflow) Ohm’slaw ConvectionͲdiffusionequation 101 0RGHOLQJ FRQGLWLRQ 1[mol/ี] 0[mol/ี] Inlet 0.1[mm/s] Outlet Normalstressiszero Wall condition Electroosmotic velcity 5HVXOW 102 Solved with COMSOL Multiphysics 5.0 Electroosmotic Micromixer 1 Introduction Microlaboratories for biochemical applications often require rapid mixing of different fluid streams. At the microscale, flow is usually highly ordered laminar flow, and the lack of turbulence makes diffusion the primary mechanism for mixing. While diffusional mixing of small molecules (and therefore of rapidly diffusing species) can occur in a matter of seconds over distances of tens of micrometers, mixing of larger molecules such as peptides, proteins, and high molecular-weight nucleic acids can require equilibration times from minutes to hours over comparable distances. Such delays are impractically long for many chemical analyses. These problems have led to an intense search for more efficient mixers for microfluidic systems. Most microscale mixing devices are either passive mixers that use geometrical stirring, or active mixers that use moving parts or external forces, such as pressure or electric field. In a passive mixer, one way of increasing the mixing is by “shredding” two or several fluids into very thin alternating layers, which decreases the average diffusion length for the molecules between the different fluids. However, these mixers often require very long mixing channels because the different fluids often run in parallel. Another way of improving mixing efficiency is to use active mixers with moving parts that stir the fluids. At the microscale level moving parts in an active mixer are very fragile. One alternative is to use electroosmotic effects to achieve a mixing effect that is perpendicular to the main direction of the flow. This model takes advantage of electroosmosis to mix fluids. The system applies a time-dependent electric field, and the resulting electroosmosis perturbs the parallel streamlines in the otherwise highly ordered laminar flow. Model Definition This example of a rather simple micromixer geometry (Figure 1) combines two fluids entering from different inlets into a single 10 μm wide channel. The fluids then enter a ring-shaped mixing chamber that has four microelectrodes placed on the outer wall at angular positions of 45, 135, −45, and −135 degrees, respectively. Assume that the 1. This model is courtesy of H. Chen, Y. T. Zhang, I. Mezic, C. D. Meinhart, and L. Petzold of the University of California, Santa Barbara (Ref. 1 and Ref. 2). 1 | 103 ELECTROOSMOTIC MICROMIXER Solved with COMSOL Multiphysics 5.0 aspect ratio (channel depth to width) is large enough that you can model the mixer using a 2D cross-sectional geometry. The material parameters relevant for the model are given in Table 1. −V0sin(ωt) V0sin(ωt) 1 2 10 μm −V0sin(ωt) 4 3 V0sin(ωt) Figure 1: Geometry of the micromixer with four symmetric electrodes on the wall of the mixing chamber. This example does not model the two inlet channels. Here you assume a parabolic inflow at the beginning of the computational domain (the gray area). The Navier-Stokes equations for incompressible flow describe the flow in the channels: ρ T ∂u – ∇ ⋅ η ( ∇u + ( ∇u ) ) + ρu ⋅ ∇ u + ∇p = 0 ∂t ∇⋅u = 0 Here η denotes the dynamic viscosity (kg/(m·s)), u is the velocity (m/s), ρ equals the fluid density (kg/m3), and p refers to the pressure (Pa). Because you do not model the two inlet channels, assume that the entrance channel starts at a position where the flow has a fully developed laminar profile. The mixed fluid flows freely out of the right end boundary, where you specify vanishing total stress components normal to the boundary: T n ⋅ [ – pI + η ( ∇u + ( ∇u ) ) ] = 0 When brought into contact with an electrolyte, most solid surfaces acquire a surface charge. In response to the spontaneously formed surface charge, a charged solution forms close to the liquid-solid interface. Known as an electric double layer, it forms because of the charged groups located on the surface that faces the solution. When the operator applies an electric field, the electric field generating the electroosmotic flow displaces the charged liquid in the electric double layer. This scheme imposes a force on the positively charged solution close to the wall surface, and the fluid starts to flow 2 | ELECTROOSMOTIC MICROMIXER 104 Solved with COMSOL Multiphysics 5.0 in the direction of the electric field. The velocity gradients perpendicular to the wall give rise to viscous transport in this direction. In the absence of other forces, the velocity profile eventually becomes almost uniform in the cross section perpendicular to the wall. This model replaces the thin electric double layer with the Helmholtz-Smoluchowski relation between the electroosmotic velocity and the tangential component of the applied electric field: εw ζ0 u = ------------ ∇TV η In this equation, εw = ε0εr denotes the fluid’s electric permittivity (F/m), ζ0 represents the zeta potential at the channel wall (V), and V equals the potential (V). This equation applies on all boundaries except for the entrance and the outlet. Assuming that there are no concentration gradients in the ions that carry the current, you can express the current balance in the channel with Ohm’s law and the balance equation for current density ∇ ⋅ ( – σ∇V ) = 0 where σ denotes conductivity (S/m) and the expression within parentheses represents the current density (A/m2). The electric potentials on the four electrodes are sinusoidal in time with the same maximum value (V0 = 0.1 V) and the same frequency (8 Hz), but they alternate in polarity. The potentials on electrodes 1 and 3 are V0sin(2πft), whereas those on electrodes 2 and 4 are −V0sin(2πft) (see Figure 1). Assume all other boundaries are insulated. The insulation boundary condition – σ∇ V ⋅ n = 0 sets the normal component of the electric field to zero. At the upper half of the inlet (see Figure 1) the solute has a given concentration, c0; at the lower half the concentration is zero. Thus, assume that the concentration changes abruptly from zero to c0 at the middle of the inlet boundary. The mixed solution flows out from the right outlet by convection, and all other boundaries are assumed insulated. Inside the mixer, the following convection-diffusion equation describes the concentration of the dissolved substances in the fluid: 3 | 105 ELECTROOSMOTIC MICROMIXER Solved with COMSOL Multiphysics 5.0 ∂c ----- + ∇ ⋅ ( – D∇c ) = R – u ⋅ ∇c ∂t (1) Here c is the concentration, D represents the diffusion coefficient, R denotes the reaction rate, and u equals the flow velocity. In this model R = 0 because the concentration is not affected by any reactions. TABLE 1: MODEL INPUT DATA PARAMETER VALUE ρ η 1000 kg/m3 10-3 Pa·s DESCRIPTION Dynamic viscosity of the fluid U0 0.1 mm/s Average velocity through the inlet εr 80.2 Relative electric permittivity of the fluid ζ -0.1 V Zeta potential on the wall-fluid boundary σ 0.11845 S/m Conductivity of the ionic solution D 10-11 m2/s Diffusion coefficient c0 1 mol/m3 Initial concentration Density of the fluid Results and Discussion Figure 2 shows a typical instantaneous streamline pattern. It reveals that electroosmotic recirculation of the fluid vigorously stirs the flow, typically in the form of two rotating vortices near the electrodes. The fundamental processes of effective mixing involve a combination of repeated stretching and folding of fluid elements in combination with diffusion at small scales. As the system applies the AC field (Figure 3), the resulting electroosmotic flow perturbs the laminar pressure-driven flow such that it pushes the combined stream pattern up and down at the beginning of the mixing chamber, causing extensive folding and stretching of material lines. 4 | ELECTROOSMOTIC MICROMIXER 106 Solved with COMSOL Multiphysics 5.0 Figure 2: Fluid streamlines in an electroosmotic micromixer at t = 0.0375 s. Figure 3: Electric potential lines for an electroosmotic micromixer. The contour lines show the shape when the device uses maximal potentials (±V0). 5 | 107 ELECTROOSMOTIC MICROMIXER Solved with COMSOL Multiphysics 5.0 The following plots further exemplify how the mixer operates. Figure 4 shows the concentration at steady state when the electric field is not applied. The flow is laminar and the diffusion coefficient is very small, so the two fluids are well separated also at the outlet. When the alternating electric field is applied, the mixing increases considerably owing to the alternating swirls in the flow. Figure 5 depicts the system at the instant when the electric field and the electroosmotic velocity have their largest magnitudes during the cycle (that is, when |sin ωt| = 1). From the plot you can estimate that the concentration at the output fluctuates with the same frequency as the electric field. Thus, this mixer should be further improved to get a steadier output. Figure 4: Steady-state solution in the absence of an electric field. 6 | ELECTROOSMOTIC MICROMIXER 108 Solved with COMSOL Multiphysics 5.0 Figure 5: Time-dependent solution at the time when the alternating electric field has its largest magnitude. This example demonstrates a rather simple and effective use of electrokinetic forces for mixing. The scheme is easy to implement, and you can easily control both the amplitude and the frequency. At low Reynold numbers the inertial forces are small, which makes it possible to calculate stationary streamlines patterns using the parametric solver to control amplitude. Notes About the COMSOL Implementation Cummings and others (Ref. 3) have shown that in order to use the Helmholtz-Smoluchowski equation at the fluid-solid boundaries, the electric field must be at least quasi-static to neglect transient effects. In other words, the time scale of the unsteady electric field must be much larger than that of the transient flow. Y. T. Zhang and others (Ref. 1) estimated that the time scale of the transient effect in the modeled micromixer (with a channel width of 10 microns) is roughly 0.0127 s. In this simulation the frequency of the applied electric potential is 8 Hz, which corresponds to a time scale of the electric field 10 times larger than that of the flow. 7 | 109 ELECTROOSMOTIC MICROMIXER Solved with COMSOL Multiphysics 5.0 Because you can model the time-dependent electric field as a product of a stationary electric field and a time-dependent phase factor (sinωt), it is possible to reduce the simulation time and memory requirements by dividing the solution into two stages. In the first, calculate the amplitude of the electric potential field and the initial state for the time-dependent flow model using a stationary solver. In the second stage, you deactivate the Electric Currents interface and calculate the transient solution for the Laminar Flow and the Transport of Diluted Species interfaces. You obtain the tangential electric field components used in the electroosmotic velocity boundary condition by multiplying the stationary DC solution by sin(ωt). This approach is permissible because there is only a one-way coupling between the electric field and the fluid fields. References 1. H. Chen, Y.T. Zhang, I. Mezic, C.D. Meinhart, and L. Petzold, “Numerical Simulation of an Electroosmotic Micromixer,” Proc Microfluidics 2003 (ASME IMECE), 2003. 2. Y.T. Zhang, H. Chen, I. Mezic, C.D. Meinhart, L. Petzold, and N.C. MacDonald, “SOI Processing of a Ring Electrokinetic Chaotic Micromixer,” Proc NSTI Nanotechnology Conference and Trade Show (Nanotech 2004), vol. 1, pp. 292–295, 2004. 3. E. Cummings, S. Griffiths, R. Nilson, and P. Paul, “Conditions for Similitude Between the Fluid Velocity and the Electric Field in Electroosmotic Flow,” Anal. Chem., vol. 72, pp. 2526–2532, 2000. Model Library path: Microfluidics_Module/Micromixers/ electroosmotic_mixer Modeling Instructions From the File menu, choose New. NEW 1 In the New window, click Model Wizard. 8 | ELECTROOSMOTIC MICROMIXER 110 Solved with COMSOL Multiphysics 5.0 MODEL WIZARD 1 In the Model Wizard window, click 2D. 2 In the Select physics tree, select Fluid Flow>Single-Phase Flow>Laminar Flow (spf). 3 Click Add. 4 In the Select physics tree, select AC/DC>Electric Currents (ec). 5 Click Add. 6 In the Select physics tree, select Chemical Species Transport>Transport of Diluted Species (tds). 7 Click Add. 8 Click Study. 9 In the Select study tree, select Preset Studies for Selected Physics Interfaces>Stationary. 10 Click Done. DEFINITIONS Parameters 1 On the Model toolbar, click Parameters. 2 In the Settings window for Parameters, locate the Parameters section. 9 | 111 ELECTROOSMOTIC MICROMIXER Solved with COMSOL Multiphysics 5.0 3 In the table, enter the following settings: Name Expression Value Description U0 0.1[mm/s] 1.0000E-4 m/s Mean inflow velocity sigma_w 0.11845[S/m] 0.11845 S/m Conductivity of the ionic solution eps_r 80.2 80.200 Relative permittivity of the fluid zeta -0.1[V] -0.10000 V Zeta potential V0 0.1[V] 0.10000 V Maximum value of the AC potential omega 2*pi[rad]*8[Hz ] 50.265 Hz Angular frequency of the AC potential t 0[s] 0.0000 s Start time D 1e-11[m^2/s] 1.0000E-11 m²/s Diffusion coefficient of the solution c0 1[mol/m^3] 1.0000 mol/m³ Initial concentration You need the constant t (used in the scalar expressions below) when first solving the model using a stationary solver. In the time-dependent simulation, the internal time variable, t, overwrites this constant (the red color is just a warning signaling that t is an internal variable). Now define a smoothed step function that you will later use to impose a step in the concentration in the middle of the channel entrance. Step 1 (step1) 1 On the Model toolbar, click Functions and choose Global>Step. 2 In the Settings window for Step, click to expand the Smoothing section. 3 In the Size of transition zone text field, type 0.1e-6. GEOMETRY 1 1 In the Model Builder window, under Component 1 (comp1) click Geometry 1. 2 In the Settings window for Geometry, locate the Units section. 3 From the Length unit list, choose μm. Rectangle 1 (r1) 1 On the Geometry toolbar, click Primitives and choose Rectangle. 2 In the Settings window for Rectangle, locate the Size section. 3 In the Width text field, type 80. 10 | ELECTROOSMOTIC MICROMIXER 112 Solved with COMSOL Multiphysics 5.0 4 In the Height text field, type 10. 5 Locate the Position section. From the Base list, choose Center. 6 Click the Build Selected button. Circle 1 (c1) 1 On the Geometry toolbar, click Primitives and choose Circle. 2 In the Settings window for Circle, locate the Size and Shape section. 3 In the Radius text field, type 15. 4 Click the Build Selected button. Circle 2 (c2) 1 On the Geometry toolbar, click Primitives and choose Circle. 2 In the Settings window for Circle, locate the Size and Shape section. 3 In the Radius text field, type 5. 4 Click the Build Selected button. Compose 1 (co1) 1 On the Geometry toolbar, click Booleans and Partitions and choose Compose. 2 Click in the Graphics window and then press Ctrl+A to select all objects. 3 In the Settings window for Compose, locate the Compose section. 4 In the Set formula text field, type (r1+c1)-c2. 5 Clear the Keep interior boundaries check box. 6 Click the Build Selected button. To add vertices for the electrode endpoints on the outer boundary, first add a square whose boundaries intersect the outer circle at the desired locations. Square 1 (sq1) 1 On the Geometry toolbar, click Primitives and choose Square. 2 In the Settings window for Square, locate the Size section. 3 In the Side length text field, type 22.27. 4 Locate the Position section. From the Base list, choose Center. 11 | 113 ELECTROOSMOTIC MICROMIXER Solved with COMSOL Multiphysics 5.0 5 Click the Build Selected button. Next, remove the parts of the square not contained inside the mixer geometry. Compose 2 (co2) 1 On the Geometry toolbar, click Booleans and Partitions and choose Compose. 2 Select both objects (co1 and sq1). 3 In the Settings window for Compose, locate the Compose section. 4 In the Set formula text field, type co1*sq1+co1. Here, co1*sq1 is the intersection of co1 and sq1. 5 Clear the Keep interior boundaries check box. 6 Click the Build Selected button. To see the effects of these operations, switch to point selection mode. 12 | ELECTROOSMOTIC MICROMIXER 114 Solved with COMSOL Multiphysics 5.0 7 Click the Select Points button on the Graphics toolbar. The model geometry is now essentially complete. However, before proceeding to the Materials branch, add an auxiliary vertex midway along the inlet boundary for use when creating the mesh. Point 1 (pt1) 1 On the Geometry toolbar, click Primitives and choose Point. 2 In the Settings window for Point, locate the Point section. 3 In the x text field, type -40. 4 Click the Build Selected button. 13 | 115 ELECTROOSMOTIC MICROMIXER Solved with COMSOL Multiphysics 5.0 Form Union (fin) 1 In the Model Builder window, under Component 1 (comp1)>Geometry 1 right-click Form Union (fin) and choose Build Selected. MATERIALS Material 1 (mat1) 1 In the Model Builder window, under Component 1 (comp1) right-click Materials and choose Blank Material. 2 In the Settings window for Material, locate the Material Contents section. 3 In the table, enter the following settings: Property Name Value Unit Density rho 1e3[kg/m^3] Property group kg/m³ Basic Dynamic viscosity mu 1e-3[Pa*s] Pa·s Basic Electrical conductivity sigma sigma_w S/m Basic Relative permittivity epsilonr eps_r 1 Basic LAMINAR FLOW (SPF) 1 In the Model Builder window’s toolbar, click the Show button and select Discretization in the menu. 14 | ELECTROOSMOTIC MICROMIXER 116 Solved with COMSOL Multiphysics 5.0 2 In the Model Builder window, under Component 1 (comp1) click Laminar Flow (spf). 3 In the Settings window for Laminar Flow, click to expand the Discretization section. 4 From the Discretization of fluids list, choose P2+P1. Using higher-order elements can improve the accuracy of the solution significantly for low Reynolds number flows such as those in this model. Inlet 1 1 On the Physics toolbar, click Boundaries and choose Inlet. 2 Select Boundaries 1 and 3 only. An alternative to left clicking to select these boundaries is to click the Paste Selection button in the Boundary Selection section of the Settings window and enter the boundary numbers in the dialog box that appears. Another possibility is to copy the text '1 and 3' from this document, click in the Selection box, and then press Ctrl+V. 3 In the Settings window for Inlet, locate the Boundary Condition section. 4 From the list, choose Laminar inflow. 5 Locate the Laminar Inflow section. In the Uav text field, type U0. 6 Select the Constrain outer edges to zero check box. Outlet 1 1 On the Physics toolbar, click Boundaries and choose Outlet. 2 Select Boundary 7 only. Wall 1 1 In the Model Builder window, under Component 1 (comp1)>Laminar Flow (spf) click Wall 1. 2 In the Settings window for Wall, locate the Boundary Condition section. 3 From the Boundary condition list, choose Electroosmotic velocity. 4 Specify the E vector as ec.Ex*sin(omega*t) x ec.Ey*sin(omega*t) y 5 From the Electroosmotic mobility list, choose Built-in expression. 6 In the ζ text field, type zeta. 7 In the εr text field, type eps_r. 15 | 117 ELECTROOSMOTIC MICROMIXER Solved with COMSOL Multiphysics 5.0 ELECTRIC CURRENTS (EC) On the Physics toolbar, click Laminar Flow (spf) and choose Electric Currents (ec). Electric Potential 1 1 On the Physics toolbar, click Boundaries and choose Electric Potential. 2 Select Boundaries 10 and 21 only. 3 In the Settings window for Electric Potential, locate the Electric Potential section. 4 In the V0 text field, type -V0. Electric Potential 2 1 On the Physics toolbar, click Boundaries and choose Electric Potential. 16 | ELECTROOSMOTIC MICROMIXER 118 Solved with COMSOL Multiphysics 5.0 2 Select Boundaries 11 and 20 only. 3 In the Settings window for Electric Potential, locate the Electric Potential section. 4 In the V0 text field, type V0. TR A N S P O R T O F D I L U T E D S P E C I E S ( T D S ) Raise the element order to match that of the Laminar Flow interface. 1 In the Model Builder window, under Component 1 (comp1) click Transport of Diluted Species (tds). 2 In the Settings window for Transport of Diluted Species, click to expand the Discretization section. 3 From the Concentration list, choose Quadratic. Transport Properties 1 1 In the Model Builder window, expand the Transport of Diluted Species (tds) node, then click Transport Properties 1. 2 In the Settings window for Transport Properties, locate the Diffusion section. 3 In the Dc text field, type D. 4 Locate the Model Inputs section. From the u list, choose Velocity field (spf). 17 | 119 ELECTROOSMOTIC MICROMIXER Solved with COMSOL Multiphysics 5.0 Concentration 1 1 On the Physics toolbar, click Boundaries and choose Concentration. 2 Select Boundaries 1 and 3 only. 3 In the Settings window for Concentration, locate the Concentration section. 4 Select the Species c check box. 5 In the c0,c text field, type c0*step1(y[1/m]). The concentration condition on Boundaries 1 and 3 gives a sharp but smooth concentration gradient in the middle of the channel entrance. Outflow 1 1 On the Physics toolbar, click Boundaries and choose Outflow. 2 Select Boundary 7 only. MESH 1 Size 1 In the Model Builder window, under Component 1 (comp1) right-click Mesh 1 and choose Free Triangular. 2 In the Settings window for Size, locate the Element Size section. 3 From the Predefined list, choose Extra fine. Size 1 1 In the Model Builder window, under Component 1 (comp1)>Mesh 1 right-click Free Triangular 1 and choose Size. 2 In the Settings window for Size, locate the Geometric Entity Selection section. 3 From the Geometric entity level list, choose Boundary. 4 Select Boundaries 10, 11, 20, and 21 only. 5 Locate the Element Size section. Click the Custom button. 6 Locate the Element Size Parameters section. Select the Maximum element size check box. 7 In the associated text field, type 0.2. 8 Select the Maximum element growth rate check box. 9 In the associated text field, type 1.1. Size 2 1 Right-click Free Triangular 1 and choose Size. 18 | ELECTROOSMOTIC MICROMIXER 120 Solved with COMSOL Multiphysics 5.0 2 In the Settings window for Size, locate the Geometric Entity Selection section. 3 From the Geometric entity level list, choose Point. 4 Select Point 2 only. 5 Locate the Element Size section. Click the Custom button. 6 Locate the Element Size Parameters section. Select the Maximum element size check box. 7 In the associated text field, type 0.1. 8 Select the Maximum element growth rate check box. 9 In the associated text field, type 1.1. 10 Click the Build All button. STUDY 1 Set up the study to start by computing the stationary solution for velocity, pressure, concentration, and electric potential. Then, add a transient simulation stage that solves only for the variables of the Laminar Flow and Transport of Diluted Species interfaces. Begin by adding a study step for the transient part. Step 2: Time Dependent 1 On the Study toolbar, click Study Steps and choose Time Dependent>Time Dependent. 19 | 121 ELECTROOSMOTIC MICROMIXER Solved with COMSOL Multiphysics 5.0 2 In the Settings window for Time Dependent, locate the Study Settings section. 3 In the Times text field, type range(0,0.125/60,0.5). 4 Locate the Physics and Variables Selection section. In the table, enter the following settings: Physics interface Solve for Discretization Electric Currents × physics 5 In the Model Builder window, click Study 1. 6 In the Settings window for Study, locate the Study Settings section. 7 Clear the Generate default plots check box. This is convenient if you want to create specialized plots while keeping the number of plot groups down. 8 On the Study toolbar, click Compute. RESULTS The following instructions show how to reproduce the plots in the Results and Discussion section. 2D Plot Group 1 1 On the Model toolbar, click Add Plot Group and choose 2D Plot Group. 2 In the Settings window for 2D Plot Group, locate the Data section. 3 From the Time (s) list, choose 0.037500. 4 Right-click Results>2D Plot Group 1 and choose Streamline. 5 In the Settings window for Streamline, locate the Streamline Positioning section. 6 From the Positioning list, choose Uniform density. 7 In the Separating distance text field, type 0.01. 8 On the 2D plot group toolbar, click Plot. 9 Click the Zoom Extents button on the Graphics toolbar. 10 Click the Zoom In button on the Graphics toolbar. Compare the result with Figure 2. 2D Plot Group 2 1 On the Model toolbar, click Add Plot Group and choose 2D Plot Group. 2 In the Settings window for 2D Plot Group, locate the Data section. 3 From the Time (s) list, choose 0.037500. 20 | ELECTROOSMOTIC MICROMIXER 122 Solved with COMSOL Multiphysics 5.0 4 Right-click Results>2D Plot Group 2 and choose Contour. 5 In the Settings window for Contour, click Replace Expression in the upper-right corner of the Expression section. From the menu, choose Component 1>Electric Currents>Electric>V - Electric potential. 6 On the 2D plot group toolbar, click Plot. Compare the result with Figure 3. 2D Plot Group 3 1 On the Model toolbar, click Add Plot Group and choose 2D Plot Group. 2 In the Model Builder window, under Results right-click 2D Plot Group 3 and choose Surface. 3 In the Settings window for Surface, click Replace Expression in the upper-right corner of the Expression section. From the menu, choose Component 1>Transport of Diluted Species>c - Concentration. 4 In the Model Builder window, right-click 2D Plot Group 3 and choose Streamline. 5 In the Settings window for Streamline, locate the Streamline Positioning section. 6 From the Positioning list, choose Uniform density. 7 In the Separating distance text field, type 0.01. 8 In the Model Builder window, click 2D Plot Group 3. 9 In the Settings window for 2D Plot Group, locate the Data section. 10 From the Time (s) list, choose 0.0000. 11 On the 2D plot group toolbar, click Plot. 12 Click the Zoom Extents button on the Graphics toolbar. 13 Click the Zoom In button on the Graphics toolbar. Compare the result with Figure 4. 14 From the Time (s) list, choose 0.46875. 15 On the 2D plot group toolbar, click Plot. Compare the result with Figure 5. 21 | 123 ELECTROOSMOTIC MICROMIXER Solved with COMSOL Multiphysics 5.0 22 | ELECTROOSMOTIC MICROMIXER 124 Fluid-Structure Interaction 125 )OXLG6WUXFWXUH,QWHUDFWLRQ 0RGHO Fluid Flow Solid 126 3K\VLFV SolidMechnics +LaminarFlow+MovingMesh=FluidͲStructureInteraction NavierͲStokesequations Inletvelocity FluidͲsolidinterface 0RGHOLQJ FRQGLWLRQ Flow Fluid Fixed Solid Inlet U*t^2/sqrt(t^4Ͳ0.07[s^2]*t^2+0.0016[s^4])[m/s] Outlet 0[Pa] 127 5HVXOW 128 Solved with COMSOL Multiphysics 5.0 Fluid-Structure Interaction Introduction The following example demonstrates techniques for modeling fluid-structure interactions in COMSOL Multiphysics. It illustrates how fluid flow can deform structures and how to solve for the flow in a continuously deforming geometry using the arbitrary Lagrangian-Eulerian (ALE) technique. The model geometry consists of a horizontal flow channel in the middle of which is an obstacle, a narrow vertical structure (Figure 1). The fluid flows from left to right, except where the obstacle forces it into a narrow path in the upper part of the channel, and it imposes a force on the structure’s walls resulting from the viscous drag and fluid pressure. The structure, being made of a deformable material, bends under the applied load. Consequently, the fluid flow also follows a new path, so solving the flow in the original geometry would generate incorrect results. The ALE method handles the dynamics of the deforming geometry and the moving boundaries with a moving grid. COMSOL Multiphysics computes new mesh coordinates on the channel area based on the movement of the structure’s boundaries and mesh smoothing. The Navier-Stokes equations that solve the flow are formulated for these moving coordinates. The structural mechanics portion of the model does not require the ALE method, and COMSOL Multiphysics solves it in a fixed coordinate system as usual. However, the strains the model computes in this way are the only source for computing the deformed coordinates with ALE. 1 | 129 FLUID-STRUCTURE INTERACTION Solved with COMSOL Multiphysics 5.0 Figure 1: Fluid flows into this horizontal flow channel from the left, and it enters with a parabolic velocity profile. A narrow vertical structure in the channel (the straight vertical structure) forces the flow into a narrow path. Due to fluid pressure and viscous drag, the originally vertical structure bends. This simulation models the fluid flow in a deformed, moving mesh that follows the movement of the bending structure. Model Definition In this example the flow channel is 100 μm high and 300 μm long. The vertical structure—5 μm wide, 50 μm high, and with a semicircular top—sits 100 μm away from the channel’s left boundary. Assume that the structure is long in the direction perpendicular to the image. The fluid is a water-like substance with a density ρ = 1000 kg/m3 and dynamic viscosity η = 0.001 Pa·s. To demonstrate the desired techniques, assume the structure consists of a flexible material with a density ρ = 7850 kg/m3 and Young’s modulus E = 200 kPa. 2 | FLUID-STRUCTURE INTERACTION 130 Solved with COMSOL Multiphysics 5.0 FLUID FLOW The fluid flow in the channel is described by the incompressible Navier-Stokes equations for the velocity field, u = (u, v), and the pressure, p, in the spatial (deformed) moving coordinate system: ρ ∂u T – ∇ ⋅ [ – p I + η ( ∇u + ( ∇u ) ) ] + ρ ( ( u – um ) ⋅ ∇ )u = F ∂t –∇ ⋅ u = 0 (1) In these equations, I denotes the unit diagonal matrix and F is the volume force affecting the fluid. Assume that no gravitation or other volume forces affect the fluid, so that F = 0. The coordinate system velocity is um = (um, vm). At the channel entrance on the left, the flow has fully developed laminar characteristics with a parabolic velocity profile but its amplitude changes with time. At first flow increases rapidly, reaching its peak value at 0.215 s; thereafter it gradually decreases to a steady-state value of 5 cm/s. The centerline velocity in the x direction, uin (see Figure 4), with the steady-state amplitude U comes from the equation 2 U⋅t u in = ----------------------------------------------------------2 2 2 ( 0.04 – t ) + ( 0.1t ) (2) where t must be expressed in seconds. At the outflow (right-hand boundary), the condition is p = 0. On the solid (nondeforming) walls, no-slip conditions are imposed, u = 0, v = 0, while on the deforming interface the velocities equal the deformation rate, u0 = ut and v0 = vt (the default condition; note that u and v on the right-hand sides refer to the displacement components). STRUCTURAL MECHANICS The structural deformations are solved for using an elastic formulation and a nonlinear geometry formulation to allow large deformations. The obstacle is fixed to the bottom of the fluid channel. All other object boundaries experience a load from the fluid, given by T F T = – n ⋅ ( – p I + η ( ∇u + ( ∇u ) ) ) (3) where n is the normal vector to the boundary. This load represents a sum of pressure and viscous forces. 3 | 131 FLUID-STRUCTURE INTERACTION Solved with COMSOL Multiphysics 5.0 MOVING MESH The Navier-Stokes equations are solved on a freely moving deformed mesh, which constitutes the fluid domain. The deformation of this mesh relative to the initial shape of the domain is computed using Winslow smoothing. This is the default smoothing when using the Fluid-Structure Interaction interface. For more information, please refer to the Fluid-Structure Interaction interface in the MEMS Module User’s Guide. Inside the obstacle, the moving mesh follows the deformations of the obstacle. At the exterior boundaries of the flow domain, the deformation is set to zero in all directions. Results and Discussion Figure 2 shows the geometry deformation and flow at t = 4 s when the system is close to its steady state. Due to the channel’s small dimensions, the Reynolds number of the flow is small (Re << 100), and the flow stays laminar in most of the area. The swirls are restricted to a small area behind the structure. The amount of deformation as well as the size and location of the swirls depend on the magnitude of the inflow velocity. Figure 2: Flow velocity and geometry deformation at t = 4 s. The streamlines indicate the flow direction and the color indicates flow-velocity magnitude. Figure 3 shows the mesh velocity at t = 0.15 s. The boundaries of the narrow structure are the only moving boundaries of the flow channel. Therefore the mesh velocity also 4 | FLUID-STRUCTURE INTERACTION 132 Solved with COMSOL Multiphysics 5.0 has its largest values near the structure. Depending on the current state of the deformation—whether it is increasing, decreasing or stationary—the mesh velocity can have a very different distribution. Figure 4 further illustrates this point; it compares the average inflow velocity to the horizontal mesh velocity and the horizontal mesh displacement just beside the top of the structure. Most of the time the deformation follows the inflow velocity quite closely. Whenever the inflow velocity starts to decrease, the deformation also decreases, which you can observe as the negative values on the horizontal mesh velocity. Toward the end of the simulation, when inflow and structure deformation approach their steady-state values, the mesh velocity also decreases to zero. Figure 3: Mesh velocity (arrows) and mesh and geometry deformation at t = 0.15 s. 5 | 133 FLUID-STRUCTURE INTERACTION Solved with COMSOL Multiphysics 5.0 Figure 4: Inflow velocity, horizontal mesh velocity, and mesh deformation. The blue curve shows the average x direction velocity at the inflow boundary (m/s); the green shows 104× mesh displacement in the x direction (dx_ale; m) at the geometry point (1.05·10-4, 0.5·10-4); and the red curve shows 103× mesh velocity in the x direction (xt; m/ s), also at the point (1.05·10-4, 0.5·10-4). Figure 5 compares the meshes at different times. The first image shows the initial mesh, which you generate prior to solving the model. This mesh is equally distributed around the top of the structure. The second image shows the mesh in its deformed form. Because the structure deforms more in the horizontal direction, the mesh also 6 | FLUID-STRUCTURE INTERACTION 134 Solved with COMSOL Multiphysics 5.0 changes more in this direction: On the left, the mesh elements are stretched; on the right, they are compressed in the x direction. Figure 5: Geometry and mesh near the top of the structure at t = 0 s and 2 s. Notes About the COMSOL Implementation This example implements the model using Fluid-Structure Interaction interface. By default the Fluid-Structure Interaction interface treats all domains as fluid. Activate solid material model node in the area of the narrow structure. To get a more accurate computation of the large strains, large deformation analysis is the default setting. The interface automatically identifies the fluid-solid interaction boundaries and assigns the boundary condition to those boundaries. Model Library path: MEMS_Module/Microfluidics/ fluid_structure_interaction Modeling Instructions From the File menu, choose New. NEW 1 In the New window, click Model Wizard. MODEL WIZARD 1 In the Model Wizard window, click 2D. 2 In the Select physics tree, select Fluid Flow>Fluid-Structure Interaction (fsi). 7 | 135 FLUID-STRUCTURE INTERACTION Solved with COMSOL Multiphysics 5.0 3 Click Add. 4 Click Study. 5 In the Select study tree, select Preset Studies>Time Dependent. 6 Click Done. DEFINITIONS Parameters 1 On the Model toolbar, click Parameters. 2 In the Settings window for Parameters, locate the Parameters section. 3 In the table, enter the following settings: Name Expression Value Description U 3.33[cm/s] 0.033300 m/s Inlet mean velocity at steady state H 100[um] 1.0000E-4 m Channel height Variables 1 1 On the Model toolbar, click Variables and choose Global Variables. 2 In the Settings window for Variables, locate the Variables section. 3 In the table, enter the following settings: Name Expression Unit Description u_mean U*t^2/ sqrt(t^4-0.07[s^2]* t^2+0.0016[s^4]) m/s Inlet mean velocity GEOMETRY 1 1 In the Model Builder window, under Component 1 (comp1) click Geometry 1. 2 In the Settings window for Geometry, locate the Units section. 3 From the Length unit list, choose μm. Rectangle 1 (r1) 1 On the Geometry toolbar, click Primitives and choose Rectangle. 2 In the Settings window for Rectangle, locate the Size section. 3 In the Width text field, type 300. 4 In the Height text field, type H. 5 Click the Build All Objects button. 8 | FLUID-STRUCTURE INTERACTION 136 Solved with COMSOL Multiphysics 5.0 Rectangle 2 (r2) 1 On the Geometry toolbar, click Primitives and choose Rectangle. 2 In the Settings window for Rectangle, locate the Size section. 3 In the Width text field, type 5. 4 In the Height text field, type 47.5. 5 Locate the Position section. In the x text field, type 100. 6 Click the Build All Objects button. Fillet 1 (fil1) 1 On the Geometry toolbar, click Fillet. 2 On the object r2, select Points 3 and 4 only. 3 In the Settings window for Fillet, locate the Radius section. 4 In the Radius text field, type 2.5. 5 Click the Build All Objects button. The geometry should look like that in the figure below. By default the Fluid-Structure Interaction interface treats all domains as fluid. Add the appropriate domain selection to the default node for the solid domain and proceed to the material specification. 9 | 137 FLUID-STRUCTURE INTERACTION Solved with COMSOL Multiphysics 5.0 FLUID-STRUCTURE INTERACTION (FSI) Linear Elastic Material 1 1 In the Model Builder window, expand the Component 1 (comp1)>Fluid-Structure Interaction (fsi) node, then click Linear Elastic Material 1. 2 Select Domain 2 only. MATERIALS Material 1 (mat1) 1 In the Model Builder window, under Component 1 (comp1) right-click Materials and choose Blank Material. 2 Select Domain 1 only. 3 In the Settings window for Material, locate the Material Contents section. 4 In the table, enter the following settings: Property Name Value Unit Property group Density rho 1e3 kg/m³ Basic Dynamic viscosity mu 1e-3 Pa·s Basic Material 2 (mat2) 1 In the Model Builder window, right-click Materials and choose Blank Material. 2 Select Domain 2 only. 3 In the Settings window for Material, locate the Material Contents section. 4 In the table, enter the following settings: Property Name Value Unit Property group Young's modulus E 2e5 Pa Basic Poisson's ratio nu 0.33 1 Basic Density rho 7850 kg/m³ Basic FLUID-STRUCTURE INTERACTION (FSI) 1 In the Model Builder window, under Component 1 (comp1) click Fluid-Structure Interaction (fsi). 2 In the Settings window for Fluid-Structure Interaction, locate the Physical Model section. 3 From the Compressibility list, choose Incompressible flow. 10 | FLUID-STRUCTURE INTERACTION 138 Solved with COMSOL Multiphysics 5.0 4 Locate the Free Deformation Settings section. From the Mesh smoothing type list, choose Hyperelastic. Inlet 1 1 On the Physics toolbar, click Boundaries and choose Inlet. 2 Select Boundary 1 only. 3 In the Settings window for Inlet, locate the Velocity section. 4 In the U0 text field, type u_mean*6*(H-Y)*Y/H^2. This gives a parabolic velocity profile with the specified mean velocity appropriate for laminar inflow. If you have a license for the CFD Module or Microfluidics Module, you can use the predefined Laminar inflow boundary condition with average velocity u_mean a boundary condition that works for general inlet shapes. Outlet 1 1 On the Physics toolbar, click Boundaries and choose Outlet. 2 Select Boundary 8 only. Fixed Constraint 1 1 On the Physics toolbar, click Boundaries and choose Fixed Constraint. 2 Select Boundary 5 only. MESH 1 Free Triangular 1 1 In the Model Builder window, under Component 1 (comp1) right-click Mesh 1 and choose Free Triangular. 2 In the Settings window for Free Triangular, locate the Domain Selection section. 3 From the Geometric entity level list, choose Entire geometry. Size 1 In the Model Builder window, under Component 1 (comp1)>Mesh 1 click Size. 2 In the Settings window for Size, locate the Element Size section. 3 From the Predefined list, choose Fine. 4 From the Calibrate for list, choose Fluid dynamics. 5 Click the Build All button. 11 | 139 FLUID-STRUCTURE INTERACTION Solved with COMSOL Multiphysics 5.0 STUDY 1 Step 1: Time Dependent 1 In the Model Builder window, expand the Study 1 node, then click Step 1: Time Dependent. 2 In the Settings window for Time Dependent, locate the Study Settings section. 3 In the Times text field, type range(0,0.005,0.75) range(1,0.25,4). 4 Select the Relative tolerance check box. 5 In the associated text field, type 0.0001. 6 On the Model toolbar, click Compute. RESULTS Flow and Stress (fsi) You can ignore the non-ideal constraints related warning shown in the log. The first default plot shows the velocity field together with the von Mises stress. 1 On the 2D plot group toolbar, click Plot. 2 Click the Zoom Extents button on the Graphics toolbar. Proceed to reproduce Figure 2, which shows the streamlines instead of the arrows. 3 In the Model Builder window, expand the Flow and Stress (fsi) node. 4 Right-click Arrow Surface 1 and choose Disable. 5 Right-click Flow and Stress (fsi) and choose Streamline. 6 In the Settings window for Streamline, click Replace Expression in the upper-right corner of the Expression section. From the menu, choose Model>Component 1>Fluid-Structure Interaction (Laminar Flow)>u_fluid,v_fluid - Velocity field (Spatial). 7 Locate the Streamline Positioning section. From the Positioning list, choose Start point controlled. 8 From the Entry method list, choose Coordinates. 9 In the x text field, type 0^(range(1,15)) 125*1^(range(1,2)). 10 In the y text field, type range(0,100/14,100) 20 5. 11 Locate the Coloring and Style section. From the Color list, choose Red. 12 On the 2D plot group toolbar, click Plot. To animate flow around the structure, do the following: 12 | FLUID-STRUCTURE INTERACTION 140 Solved with COMSOL Multiphysics 5.0 Export 1 On the Results toolbar, click Player. 2 In the Settings window for Player, locate the Animation Editing section. 3 From the Time selection list, choose Interpolated. 4 In the Times (s) text field, type range(0.025,0.025,0.5). 5 Right-click Results>Export>Player 1 and choose Play. To inspect the deformed geometry and deformed mesh near the top of the structure (Figure 5), proceed with the following steps. Data Sets 1 On the Results toolbar, click More Data Sets and choose Solution. 2 On the Results toolbar, click Selection. 3 In the Settings window for Selection, locate the Geometric Entity Selection section. 4 From the Geometric entity level list, choose Domain. 5 Select Domain 2 only. 2D Plot Group 3 1 On the Results toolbar, click 2D Plot Group. 2 In the Settings window for 2D Plot Group, locate the Plot Settings section. 3 From the Frame list, choose Spatial (x, y, z). 4 Locate the Data section. From the Time (s) list, choose 0.0000. 5 Right-click Results>2D Plot Group 3 and choose Surface. 6 In the Settings window for Surface, locate the Expression section. 7 In the Expression text field, type 1. 8 Locate the Coloring and Style section. From the Coloring list, choose Uniform. 9 From the Color list, choose Blue. 10 Select the Wireframe check box. 11 Click to expand the Quality section. On the 2D plot group toolbar, click Plot. 12 In the Model Builder window, right-click 2D Plot Group 3 and choose Surface. 13 In the Settings window for Surface, locate the Data section. 14 From the Data set list, choose Study 1/Solution 1 (2). 15 From the Time (s) list, choose 0.0000. 16 Locate the Expression section. In the Expression text field, type 1. 13 | 141 FLUID-STRUCTURE INTERACTION Solved with COMSOL Multiphysics 5.0 17 Locate the Coloring and Style section. From the Coloring list, choose Uniform. Click the Zoom Box button on the Graphics toolbar and then use the mouse to zoom in on the obstacle. 1 In the Model Builder window, under Results click 2D Plot Group 3. 2 In the Settings window for 2D Plot Group, locate the Data section. 3 From the Time (s) list, choose 2.0000. 4 In the Model Builder window, under Results>2D Plot Group 3 click Surface 2. 5 In the Settings window for Surface, locate the Data section. 6 From the Time (s) list, choose 2.0000. 7 On the 2D plot group toolbar, click Plot. Add the arrow plot, to reproduce Figure 3. 8 In the Model Builder window, click 2D Plot Group 3. 9 In the Settings window for 2D Plot Group, locate the Data section. 10 From the Time (s) list, choose 0.15000. 11 In the Model Builder window, under Results>2D Plot Group 3 click Surface 2. 12 In the Settings window for Surface, locate the Data section. 13 From the Time (s) list, choose 0.15000. 14 In the Model Builder window, right-click 2D Plot Group 3 and choose Arrow Surface. 15 In the Settings window for Arrow Surface, locate the Expression section. 16 In the x component text field, type xt. 17 In the y component text field, type yt. 18 Locate the Coloring and Style section. Select the Scale factor check box. 19 In the associated text field, type 80000. 20 On the 2D plot group toolbar, click Plot. Finally, plot the horizontal mesh velocity, the mesh deformation at the point beside the top of the structure, and inflow velocity (Figure 4). 1D Plot Group 4 1 On the Model toolbar, click Add Plot Group and choose 1D Plot Group. 2 On the 1D plot group toolbar, click Global. 3 In the Settings window for Global, click Replace Expression in the upper-right corner of the y-axis data section. From the menu, choose Model>Global Definitions>Variables>u_mean - Inlet mean velocity. 14 | FLUID-STRUCTURE INTERACTION 142 Solved with COMSOL Multiphysics 5.0 4 On the 1D plot group toolbar, click Plot. Data Sets 1 On the Results toolbar, click Cut Point 2D. 2 In the Settings window for Cut Point 2D, locate the Point Data section. 3 In the x text field, type 105. 4 In the y text field, type 50. 1D Plot Group 4 1 On the 1D plot group toolbar, click Point Graph. 2 In the Settings window for Point Graph, locate the Data section. 3 From the Data set list, choose Cut Point 2D 1. 4 Locate the y-Axis Data section. In the Expression text field, type xt. 5 From the Unit list, choose mm/s. 6 Click to expand the Legends section. Select the Show legends check box. 7 From the Legends list, choose Manual. 8 In the table, enter the following settings: Legends Mesh velocity in the x direction (mm/s) 9 Right-click Results>1D Plot Group 4>Point Graph 1 and choose Duplicate. 10 In the Settings window for Point Graph, locate the y-Axis Data section. 11 In the Expression text field, type x-X. 12 From the Unit list, choose mm. 13 Locate the Legends section. In the table, enter the following settings: Legends Mesh displacement in the x direction (mm) 14 On the 1D plot group toolbar, click Plot. 15 | 143 FLUID-STRUCTURE INTERACTION Solved with COMSOL Multiphysics 5.0 16 | FLUID-STRUCTURE INTERACTION 144 ၔ༯ሂታሂ ๕ྱ৭ଌඬ࿚ัಠูལትಁເኁྮເᄸ 7 ( FRPVRO#DOWVRIWFRNU : ZZZDOWVRIWFRNU