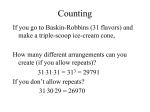Download Examples #3: Probability and statistics

Examples #3: Probability and statistics
1. A bus has 9 seats facing forward and 8 seats facing backward. In how many ways can 7 passengers be
seated if 2 refuse to ride facing forward and 3 refuse to ride facing backward?
ˆ
We have 2 passengers who must face backward (group A), 3 passengers who must face forward
(group B), and 2 passengers who don't care (group C). First, we must seat the picky passengers:
8×7
ways to seat the group A, and
9×8×7
ways to seat the group B. This takes care of 5
passengers on 5 seats. There are 12 seats left for 2 passengers of group C, so
12 × 11
dierent
seating arrangements. In total:
(8 × 7) × (9 × 8 × 7) × (12 × 11) = 3725568
acceptable seating arrangements.
2. Find the number of ways in which 8 persons can be assigned to 2 rooms (A and B) if each room must
have at least 3 people.
ˆ
The acceptable room occupancies are
(A, B) = {(3, 5), (4, 4), (5, 3)}.
In each case we are free to
pick which people go to the room A: the remaining people will go to the room B, and their order
does not matter. We use combinations. The total number of acceptable arrangements is:
8
8
8
8
8
8×7×6 8×7×6×5
+
= 112 + 70 = 182
+
+
=2
+
=2
3×2×1 4×3×2×1
4
5
3
4
3
3. Find the number of dierent words that can be made from the letters MONOTONOUS. In how many
of those words are 4 O's together next to each other? In how many of those words are 3 O's together?
ˆ
The word MONOTONOUS has 4 O's, 2 N's and one of M,T,U,S each. There are 10 letters total,
which can be permuted in 10! ways. However, some of these permutations are identical, since
exchanging the letters O among themselves (in 4!
ways) does not change the word.
Similarly,
exchanging the two N's (in 2! ways) changes nothing. Hence, the total number of dierent words
is:
10!
4! × 2!
=
=
ˆ
10 × 9 × 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1
10 × 9 × 8 × 7 × 6 × 5
=
4×3×2×1×2×1
2
10 × 9 × 4 × 7 × 6 × 5 = 10 × 9 × 7 × 120 = 1200 × 63 = 75600
If the 4 O's need to be together, treat them as one rigid symbol. There are 6 other single-character
symbol, of which one is a doublet. The total number of requested words is:
7!
7×6×5×4×3×2×1
=
= 7 × 6 × 5 × 4 × 3 = 18 × 140 = 2520
2!
2×1
ˆ
If 3 O's should stick together, think of them as a single symbol o. Without the fourth O, we
would permute the letters of MoNTNUS as above. For each permutation, there are 6 places where
we could insert the fourth O, making sure that O is not next to o (or we would have a forbidden
sequence of four O's):
OMoNTNUS, MoNOTNUS, MoNTONUS, MoNTNOUS, MoNTNUOS,
MoNTNUSO. What if o is at the beginning or the end of the template sequence, as in oMNTNUS? Still, there are 6 places where the fourth O can be inserted. Therefore, for every one of
2520 permutations of letters without the fourth O, there are 6 insertion points for the fourth O.
The total number of acceptable words is:
6 × 2520 = 15120
1
4. Three coins are tossed.
(a) Find the probability of getting no heads.
(b) Find the probability of getting at least one head.
(c) Show that the event heads on the rst coin and the event tails on the last coin are independent.
(d) Show that the event only two coins land heads and the event three coins land heads are not
independent.
ˆ
(a) All three coins must land tails, with probability 1/2. Hence,
ˆ
(b) If we get heads in either one of three tossings, the requested event happens. Counting the
P = (1/2)3 = 1/8.
ways in which this can happen is harder than observing that the requested event does not happen
only is all three tossings end with tails (i.e.
probability is:
the event from part (a) happens).
Therefore, the
P = 1 − 1/8 = 7/8.
ˆ
(c) This is obvious if the outcome of each tossing is completely random.
ˆ
(d) These two events are mutually exclusive
5. Various 6 digit numbers can be formed by permuting the digits 666655. All arrangements are equivalently likely. Given that the number is even, what is the probability that two ves are together? Hint:
You must nd a conditional probability.
ˆ
Since the number must be even, the last number is 6, and there are 4 ways to choose this number.
There are 5 digits left, and the total number of their permutations give 5!. We have to divide it
by 3! of permutations of 6 and 2! permutations between 5. We end at the number of dierent
numbers is 4
· 5!/3!2!
= 40. If we want to have two ves together, it is the same as permute 4
units, the number of permutations 4
· 4!/3! = 16. Thus the probability is P = 16/40 = 2/5 .
6. Fifteen boys go hiking. 5 get lost, 8 get sunburned, and 6 return home without problems.
(a) What is the probability that a sunburned boy got lost?
(b) What is the probability that a lost boy got sunburned?
ˆ
(a) Let us dene the event to get sunburned as A, and the event to get lost as B. The probability
P (A) = 8/15, while the probability to get lost is P (B) = 5/15 = 1/3. We
15 − 6 = 9 boys had problems. Thus, the joint probability to be either sun-burned or
P (A ∪ B) = 9/15. The probability to be both sunburned and lost is:
to get sunburned is
know that
lost is,
P (A ∩ B) = P (A) + P (B)=P (A ∪ B) = (8 + 5=9)/15 = 4/15
.Consequently, the conditional probabilities are
and
P (B|A) = P (A ∩ B)/P (B) = 4/5
for (b).
2
P (A|B) = P (A ∩ B)/P (A) = 1/2
for part (a),
7. A dice is biased so that even numbers occur 3 times as often as odd numbers.
(a) If the dice is thrown
If it is thrown
N = 120
N = 12
times, what is the probability that odd numbers occur 3 times?
times, what is the probability that odd numbers occur 30 times?
Use the
binomial distribution.
(b) Compute the same quantities as in part (a), but use the Gaussian distribution Note: For parts (a)
and (b) compute your answers to four decimal places.
ˆ
(a) In a single dice throw, the probability for an odd number is
is
q = 1 − p = 3/4.
The probability to have
(b)
PN,k =
Hence:
k
p = 1/4
3N −k
N k N −k
N!
p q
=
k!(N − k)! 4N
k
(b)
P12,3 = 0.2881
(b)
,
P120,30 = 0.0839
hki = N/4 and their variance (computed
σ 2 = N p · q = 3N/16. The Gaussian probability is:
(b) The number of odd numbers is
distribution) is
and for an even number
odd numbers according to binomial distribution is:
(g)
PN,k =
Therefore:
from the binomial
2
2
1
√ e−(k−hki) /2σ
σ 2π
(g)
P12,3 = 0.2660
(g)
,
P120,30 = 0.0841
8. A book with 700 misprints contains 1400 pages.
(a) What is the probability that one page contains no mistakes?
(b) What is the probability that one pages contains 2 mistakes?
ˆ
Let the number of pages be
mistakes on a page (up to
of
N
n).
N
and the number of mistakes
n.
There could be any number of
To enumerate all possibilities, imagine creating all possible sequences
letters P (for page) and
n
letters M (for mistake), with a meaning that if
just after a letter P, then there are
k
k
letters M come
mistakes on the page symbolized by that letter P. We must
surely start the sequence with a letter P, but otherwise we are free to arrange the remaining
n M's any way
N − 1 P's after the
(N − 1 + n)!
P's and
we want. There are
the
rst among themselves, or permuting the
N −1
possible permutations, but permuting
n
M's among themselves does
not change the sequence. The total number of sequences is:
NN,n =
(N − 1 + n)!
(N − 1)!n!
(a) If one has a page without mistakes, it means that
pages. The number of such possibilities is
NN −1,n
=
NN,n
NN −1,n
(N −2+n)!
(N −2)!n!
(N −1+n)!
(N −1)!n!
3
=
n
mistakes are distributed between
so the probability is:
N −1
= 0.67
N −1+n
N −1
(b) If we have two misprints at a page, then
n−2
misprints are distributed between
N −1
The probability is:
NN −1,n−2
=
NN,n
(N −2+n−2)!
(N −2)!(n−2)!
(N −1+n)!
(N −1)!n!
=
(N − 1)n(n − 1)
= 0.07
(N − 1 + n)(N − 2 + n)(N − 3 + n)
4
pages.