* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Angles and Equations Essential
Rotation formalisms in three dimensions wikipedia , lookup
Pythagorean theorem wikipedia , lookup
Integer triangle wikipedia , lookup
History of trigonometry wikipedia , lookup
Line (geometry) wikipedia , lookup
Rational trigonometry wikipedia , lookup
Perceived visual angle wikipedia , lookup
Multilateration wikipedia , lookup
Trigonometric functions wikipedia , lookup
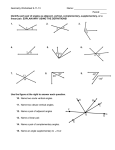
Math 7 Unit Outline Title: Angles and Equations Essential Question(s): How are the different angles created by intersecting lines related? How do I use the properties of special pairs of angles to solve problems? How do I write and solve algebraic equations to find unknown variables and angles in a figure? MCC7.G.5 Use facts about supplementary, complementary, vertical, and adjacent angles in a multi‐step problem to write and solve simple equations for an unknown angle in a figure. Assessment Description/Performance Task: Constructed response Informal assessment Performance task Selected response Brief Description: Instructional Methods Introduction to Unit: Unpack the standards with the students. Suggestion: Highlight the verbs, circle the nouns, and discuss the meaning of each word. Prompt students to circle additional words in the standards that they are unfamiliar with. Day 1: Learning Target: Today I will learn about angle pairs because intersecting lines form special relationships that help me solve problems. Launch: Have students draw/create a pair of intersecting lines (they can use spaghetti noodles, pipe cleaners, draw them individually, or the teacher can draw them on the white board or using technology). Students then measure the different angles and as a class or an individual written assignment, they discuss what they notice about the different angles. This leads into what we call the different pairs of angles. Teach: Go through the graphic organizer and answer the questions on Reading Strategies: Angles. Vocabulary Activity: Put students in pairs of groups of three. Each pair/group gets a Frayer model with one of the vocabulary words in the center (adjacent, linear pair, complementary, supplementary, vertical). They fill in only one box of the Frayer model. After a minute or two, they pass their Frayer model to another pair/group. They then fill in another box of the new Frayer model. Repeat this 4 times until all boxes are filled in. Share completed Frayer models and post outstanding ones in the room. Summary: Have students fill in the blank: I really understand ______________, but I’m still not sure about __________________. Other Suggested resources: Gizmo (Investigating Angle Theorems Activity A) at www.explorelearning.com , or create a Flip Book. Assess student understanding by having students complete Mastery Pairs of Angles WS and/or Name the Relationship WS. Day 2: Learning Target: Today I will determine angle measures from a diagram. Use the power point Determining Angle Measures of Intersecting Lines, which begins with a Do-Now or Warm-Up Teach: In the power point, students will watch a video from Khan Academy at http://www.khanacademy.org/math/geometry-1/core-geometry/v/angles-at-the-intersection-oftwo-lines . ***Please Note, if the video doesn’t play, just click the download button at the bottom right hand corner and it will download and play from there. After the video, students will go through the examples in the power point, or, you can also work through examples on the Khan Academy website at http://www.khanacademy.org/exercise/complementary_and_supplementary_angles . You can turn on the scratchpad and show work in different colors. Assess student understanding by selecting a variety of worksheets at http://www.mathworksheets4kids.com/angles.html Day 3: Learning Target: Today I will write and solve equations to find missing angle measures. CCSD Version Date: March 2012 Warm-Up/Do-Now: Students will complete the writing piece on explaining the steps of finding different angle measures. Teach: Students go through the Class Notes on writing and solving equations using angle pair relationships. There are four examples that you will work through as a class. You can do these using white boards or have students complete on their own note sheet. This was adapted from www.betterlesson.com (search for Solve Equations with Angles.) Students then work through the independent practice. Students can work individually or in pairs. A group of students may be selected to work in a group with the teacher. For co-taught classes, this is a great opportunity for parallel teaching or station teaching. Summarize: Exit Ticket/ Ticket Out the Door (if you run out of time, you can use this as a warm up the next day) Assess student understanding by the independent practice and Exit Ticket. Day 4: Learning Target: Today I will write and solve equations to find missing angle measures. Review notes and practice from the day before Activity: Scavenger Hunt: Copy the scavenger hunt on colored paper and hang the papers around the room. Instruct students to number their papers from 1 to 12 and then go with their partner to one of the colored papers. Each scavenger hunt page is divided into two sections - an answer at the top and a problem at the bottom. Students will work the problem at the bottom of the page. When they have an answer, they should look around the room to find the scavenger hunt page with that answer at the top. They should go to that scavenger hunt page and work that problem as their second problem. Students will continue in this manner until they have completed all twelve problems. After students have completed their 12th problem, they should end at the first scavenger hunt page. If they return to their first scavenger hunt page before they have completed all twelve problems, they have made an error and need to go back and check their work. Assess student understanding by observing and addressing issues that arise during the activity. If time permits, go ahead and begin the performance task for day 5. Day 5: Learning Target: Today I will create a city using my knowledge of angle pairs and their relationships. Students will complete the City Project in groups of 3 or 4. CCSD Version Date: March 2012 Name LESSON 1-4 Date Class Reading Strategies Use a Graphic Organizer The graphic organizer below outlines the different possibilities for a pair of angles. adjacent—two angles in the same plane with a common vertex and a common side but no common interior points complementary—two angles whose measures have a sum of 90 linear—adjacent angles whose noncommon sides are opposite rays vertical—two nonadjacent angles formed by two intersecting lines Angle pairs can be supplementary—two angles whose measures have a sum of 180° Identify each pair of angles as complementary, supplementary, linear, vertical, or adjacent. Use the graphic organizer above to help you. Keep in mind that there may be more than one answer for each exercise. 2. 1. complementary vertical 3. 4. supplementary linear or supplementary 5. 6. adjacent Copyright © by Holt, Rinehart and Winston. All rights reserved. complementary 34 Holt Geometry Name LESSON 1-4 Date Class Name Reteach LESSON Pairs of Angles 1-4 continued Complementary Angles Supplementary Angles sum of angle measures is 180� � � � � � � � � m�3 � m�4 � 180� m�1 � m�2 � 90� In each pair, �3 and �4 are supplementary. In each pair, �1 and �2 are complementary. Class Challenge Investigating Angle Measurement For greater accuracy in angle measurement, each degree can be divided into 60 equal parts, called minutes (1� � 60�). Each minute can be further divided into 60 equal parts, called seconds (1�� 60�). Angle Pairs sum of angle measures is 90� Date Given a decimal angle measure, you can convert it to degrees and minutes. Given an angle measure in degrees and minutes, you can convert it to a decimal measure. 67.2� � 67� � 0.2� � 67� � (0.2 � 60)� � 67� � 12�, or 67�12� 119� 51� � 119� � 51� 51 � � 119� � ___ 60 � � � 119� � 0.85�, or 119.85� Find the measure of the complement of each angle using degrees, minutes, and seconds. 2. 1. Tell whether each pair of labeled angles is complementary, supplementary, or neither. ������� 37.76° 11. 10. 52� 14� 24� ���� ���� ��� Find the measure of the supplement of each angle using degrees, minutes, and seconds. ��� complementary 5� 12� neither 4. 3. 152.375° �������� Find the measure of each of the following angles. 12. complement of �S 34� 13. supplement of �S 124� 14. complement of �R 68� 15. supplement of �R 158� 64� 48� 27� 37� 30� Use the figure for Exercises 5–8. ��� � 5. Name a pair of supplementary angles. � Sample answer: �KLM and �MLN 6. Name a pair of vertical angles whose measures have a sum that is less than 180�. ��� � � � � � � � � � � Sample answer: �KLH and �MLN 16. �LMN and �UVW are complementary. Find the measure of each angle if m�LMN � (3x � 5)� and m�UVW � 2x �. � 7. If m�HJK � (3x � 2)�, what is the measure of �KJM? 180 � (3x � 2)� or (178 � 3x)� � _ m�LMN � 56�; m�UVW � 34� 8. Suppose HQ is drawn on the figure. Name a pair of vertical angles that is formed. Sample answer: �HCK and �RCQ 31 Copyright © by Holt, Rinehart and Winston. All rights reserved. Name LESSON 1-4 Date Holt Geometry Class Problem Solving LESSON 1-4 Pairs of Angles Use the drawing of part of the Eiffel Tower for Exercises 1–5. 1. Name a pair of angles that appear to be complementary. Y 2. Name a pair of supplementary angles. Class Holt Geometry Reading Strategies Use a Graphic Organizer adjacent—two angles in the same plane with a common vertex and a common side but no common interior points A M 3. If m�CSW � 45�, what is m�JST ? How do you know? W S D J R � complementary—two angles whose measures have a sum of 90� C K Z linear—adjacent angles whose noncommon sides are opposite rays � � � B L Sample answer: �AML and �YML 45�; they are vertical angles. Date The graphic organizer below outlines the different possibilities for a pair of angles. X Sample answer: �ALB and �BLC 32 Copyright © by Holt, Rinehart and Winston. All rights reserved. Name T F vertical—two nonadjacent angles formed by two intersecting lines Angle pairs can be E ��� 4. If m�FKB � 135�, what is m�BKL? How do you know? � � supplementary—two angles whose measures have a sum of 180° ��� 45�; the angles are supplementary. ��� ��� 5. Name three angles whose measures sum to 180�. Sample answer: �ABM, �MBK, and �KBC Identify each pair of angles as complementary, supplementary, linear, vertical, or adjacent. Use the graphic organizer above to help you. Keep in mind that there may be more than one answer for each exercise. Choose the best answer. 6. A landscaper uses paving stones for a walkway. Which are possible angle measures for a� and b� so that the stones do not have space between them? A 50�, 100� C 75�, 105� B 45�, 45� D 90�, 80� �� � � H 158� G 112� J 180� complementary A �R is acute. vertical 3. 4. � ���� ��� supplementary 8. �R and �S are complementary. If m�R � (7 � 3x)� and m�S � (2x � 13)�, which is a true statement? B �R is obtuse. ��� ��� 7. The angle formed by a tree branch and the part of the trunk above it is 68�. What is the measure of the angle that is formed by the branch and the part of the trunk below it? F 22� 2. 1. �� linear or supplementary 5. C �R and �S are right angles. D m�S � m�R 6. � � ��� adjacent Copyright © by Holt, Rinehart and Winston. All rights reserved. 33 Copyright © by Holt, Rinehart and Winston. All rights reserved. � Holt Geometry Copyright © by Holt, Rinehart and Winston. All rights reserved. 66 ��� complementary 34 Holt Geometry Holt Geometry CCSD Version Date: March 2012 Describe in words Describe in words Sketch examples Sketch examples Sketch examples Sketch examples Describe in words Describe in words Name LESSON 1-4 Date Class Review for Mastery Pairs of Angles Angle Pairs Adjacent Angles have the same vertex and share a common side Linear Pairs adjacent angles whose noncommon sides are opposite rays Vertical Angles nonadjacent angles formed by two intersecting lines ⬔1 and ⬔2 are adjacent. ⬔3 and ⬔4 are adjacent and form a linear pair. ⬔5 and ⬔6 are vertical angles. Tell whether ⬔7 and ⬔8 in each figure are only adjacent, are adjacent and form a linear pair, or are not adjacent. 2. 1. 3. Tell whether the indicated angles are only adjacent, are adjacent and form a linear pair, or are not adjacent. 4. ⬔5 and ⬔4 5. ⬔1 and ⬔4 6. ⬔2 and ⬔3 Name each of the following. 7. a pair of vertical angles 8. a linear pair 9. an angle adjacent to ⬔4 Copyright © by Holt, Rinehart and Winston. All rights reserved. 30 Holt Geometry Name LESSON 1-4 Date Class Review for Mastery Pairs of Angles continued Angle Pairs Complementary Angles sum of angle measures is 90 Supplementary Angles sum of angle measures is 180 m⬔3 m⬔4 180 m⬔1 m⬔2 90 In each pair, ⬔1 and ⬔2 are complementary. In each pair, ⬔3 and ⬔4 are supplementary. Tell whether each pair of labeled angles is complementary, supplementary, or neither. 11. 10. Find the measure of each of the following angles. 12. complement of ⬔S 13. supplement of ⬔S 56° S 14. complement of ⬔R 15. supplement of ⬔R 22° R 16. ⬔LMN and ⬔UVW are complementary. Find the measure of each angle if m⬔LMN (3x 5) and m⬔UVW 2x. Copyright © by Holt, Rinehart and Winston. All rights reserved. 31 Holt Geometry LESSON 1-4 Practice A 1-4 Complete the statements. side , but no common interior points. Use the figures for Exercises 3 and 4. 90 4. complement of ⬔Y . right angle Supplementary measure of the angle. . 132 6. An angle is its own complement. Find the measure of a supplement to this angle. angles are two angles whose measures 135 have a sum of 180. 6. The kind of angle formed by the noncommon sides of two adjacent and straight angle supplementary angles is a 7. ⬔DEF and ⬔FEG are complementary. m⬔DEF (3x 4)°, and m⬔FEG (5x 6)°. Find the measures of both angles. m⬔DEF . Draw your answer in the space provided. 8. Sketch ⬔1 and ⬔2 so that they form a linear pair. Find the measures of both angles. m⬔DEF 9. Name a pair of vertical angles. Possible answers: ⬔1 and ⬔3 In an equilateral triangle, all three sides have equal lengths and all three angles have equal measures. Find the measure of the following angles. 9. supplement of ⬔A 120 30 or ⬔2 and ⬔4 10. Name a linear pair of angles. Possible answers: ⬔1 and ⬔2; ⬔2 and ⬔3; ⬔3 and ⬔4; or ⬔1 and ⬔4 ! 11. ⬔ABC and ⬔CBD form a linear pair and have equal measures. Tell if ⬔ABC is acute, right, or obtuse. Draw your answer in the space provided. 11. Sketch ⬔1 and ⬔2 so that they are vertical angles. 91; m⬔FEG 89 Use the figure for Exercises 9 and 10. In 2004, several nickels were minted to commemorate the Louisiana Purchase and Lewis and Clark’s expedition into the American West. One nickel shows a pipe and a hatchet crossed to symbolize peace between the American government and Native American tribes. 3AMPLEANSWER 10. complement of ⬔A 29; m⬔FEG 61 8. ⬔DEF and ⬔FEG are supplementary. m⬔DEF (9x 1)°, and m⬔FEG (8x 9)°. 3AMPLEANSWER 7. Sketch ⬔1 and ⬔2 so that they are adjacent angles. 3AMPLEANSWER 27 Copyright © by Holt, Rinehart and Winston. All rights reserved. Holt Geometry LESSON 1-4 Pairs of Angles 1. Draw two intersecting lines and label the resulting angles with the numbers 1, 2, 3, and 4. 2. Label ⬔1 with x . ⬔1 and ⬔2 are supplementary. Find the measure of ⬔2 and label the diagram. 45°; 45° 28 Copyright © by Holt, Rinehart and Winston. All rights reserved. Practice C Draw your answers in the space provided. right __› 12. ⬔KLM and ⬔MLN are complementary. LM bisects ⬔KLN. Find the measures of ⬔KLM and ⬔MLN. 1-4 : (110 8x) 5. An angle measures 12 degrees less than three times its supplement. Find the 4. The kind of angle formed by the noncommon sides of two adjacent and complementary angles is a 9 X 137.9 3. supplement of ⬔Z 3. Complementary angles are two angles whose measures have a sum of LESSON 180 ___› QR 2. Name the ray that ⬔PQR and ⬔SQR share. 2. A linear pair is a pair of adjacent angles whose noncommon sides are opposite rays. 5. Pairs of Angles 1. ⬔PQR and ⬔SQR form a linear pair. Find the sum of their measures. vertex 1. Adjacent angles are two angles in the same plane with a common and a common Practice B LESSON Pairs of Angles Holt Geometry Review for Mastery Pairs of Angles Angle Pairs 3AMPLEANSWER X X X Adjacent Angles have the same vertex and share a common side Linear Pairs adjacent angles whose noncommon sides are opposite rays Vertical Angles nonadjacent angles formed by two intersecting lines 3. ⬔3 is also supplementary to ⬔2. Find the measure of ⬔3 and label the diagram. 4. From your work in Exercises 1–3, make a conclusion about the measures of the vertical angles. The measures of the vertical angles are equal. ⬔1 and ⬔2 are adjacent. 5. ⬔X is complementary to ⬔Y, and ⬔Z is also complementary to ⬔Y. Explain why ⬔X and ⬔Z are congruent. ⬔3 and ⬔4 are adjacent and form a linear pair. ⬔5 and ⬔6 are vertical angles. Tell whether ⬔7 and ⬔8 in each figure are only adjacent, are adjacent and form a linear pair, or are not adjacent. If m⬔X m⬔Y 90 and m⬔Z m⬔Y 90, then m⬔X and m⬔Z 2. 1. are both equal to 90 m⬔Y. So m⬔X m⬔Z. Two angles whose measures are equal are congruent. Adjacent angles are defined as two angles in the same plane with a common vertex and a common side, but no common interior points. adjacent and form a linear pair 6. ⬔ADB and ⬔CDB are adjacent angles. If the phrase “but no common interior points” was not part of the definition, name another pair of angles that would qualify as adjacent. 3. only adjacent not adjacent Tell whether the indicated angles are only adjacent, are adjacent and form a linear pair, or are not adjacent. Possible answer: ⬔ADB and ⬔ADC only adjacent 4. ⬔5 and ⬔4 Draw your answer in the space provided. 7. Draw a diagram that shows why the definition of adjacent angles includes the phrase “in the same plane.” 5. ⬔1 and ⬔4 not adjacent 6. ⬔2 and ⬔3 adjacent and form a linear pair Use the figure for Exercises 8 –10. This diagram shows a ray of light reflecting off a mirror. When light reflects, the incident angle and the reflected angle are congruent, that is, ⬔1 ⬔2. Find the measure of ⬔1 in each situation below. 8. ⬔1 ⬔3 9. ⬔3 is a right angle 60 Copyright © by Holt, Rinehart and Winston. All rights reserved. 45 29 Copyright © by Holt, Rinehart and Winston. All rights reserved. Name each of the following. 7. a pair of vertical angles 10. m⬔1 2m⬔3 8. a linear pair Possible answers: ⬔1 and ⬔6, ⬔2 and ⬔5 Possible answers: ⬔1 and ⬔2; ⬔1 and ⬔5; ⬔5 and ⬔6; ⬔6 and ⬔2 72 9. an angle adjacent to ⬔4 Holt Geometry Copyright © by Holt, Rinehart and Winston. All rights reserved. 65 001_072_Go08an_CRF_c01.indd 30 ⬔3 30 Holt Geometry Holt Geometry 3/23/07 2:36:22 PM LESSON 1-4 Review for Mastery Pairs of Angles LESSON 1-4 continued For greater accuracy in angle measurement, each degree can be divided into 60 equal parts, called minutes (1 60). Each minute can be further divided into 60 equal parts, called seconds (1 60 ). Angle Pairs Complementary Angles sum of angle measures is 90 Supplementary Angles sum of angle measures is 180 Given an angle measure in degrees and minutes, you can convert it to a decimal measure. 67.2 67 0.2 119 51 119 51 51 119 ___ 60 67 (0.2 60) 67 12, or 6712 In each pair, ⬔3 and ⬔4 are supplementary. In each pair, ⬔1 and ⬔2 are complementary. Given a decimal angle measure, you can convert it to degrees and minutes. m⬔3 m⬔4 180 m⬔1 m⬔2 90 Challenge Investigating Angle Measurement 119 0.85, or 119.85 Find the measure of the complement of each angle using degrees, minutes, and seconds. 2. 1. Tell whether each pair of labeled angles is complementary, supplementary, or neither. 37.76° 11. 10. 52 14 24 5 12 Find the measure of the supplement of each angle using degrees, minutes, and seconds. complementary neither 4. 3. 152.375° Find the measure of each of the following angles. 12. complement of ⬔S 34 13. supplement of ⬔S 124 27 37 30 Use the figure for Exercises 5–8. 56° 14. complement of ⬔R 68 15. supplement of ⬔R 158 64 48 S 5. Name a pair of supplementary angles. + Sample answer: ⬔KLM and ⬔MLN 6. Name a pair of vertical angles whose measures have a sum that is less than 180 . 22° R & , * ( - # ' 0 . Sample answer: ⬔KLH and ⬔MLN 16. ⬔LMN and ⬔UVW are complementary. Find the measure of each angle if m⬔LMN (3x 5) and m⬔UVW 2x . 7. If m⬔HJK (3x 2), what is the measure of ⬔KJM? 1 180 (3x 2) or (178 3x) 2 _ m⬔LMN 56; m⬔UVW 34 8. Suppose HQ is drawn on the figure. Name a pair of vertical angles that is formed. Sample answer: ⬔HCK and ⬔RCQ 31 Copyright © by Holt, Rinehart and Winston. All rights reserved. LESSON 1-4 001_072_Go08an_CRF_c01.indd 31 Holt Geometry Problem Solving LESSON 1-4 Pairs of Angles 4/11/07 3:08:19 PM Use the drawing of part of the Eiffel Tower for Exercises 1–5. 1. Name a pair of angles that appear to be complementary. Holt Geometry Reading Strategies Use a Graphic Organizer The graphic organizer below outlines the different possibilities for a pair of angles. adjacent—two angles in the same plane with a common vertex and a common side but no common interior points X Sample answer: ⬔ALB and ⬔BLC 32 Copyright © by Holt, Rinehart and Winston. All rights reserved. Y A M 2. Name a pair of supplementary angles. B L Sample answer: ⬔AML and ⬔YML linear—adjacent angles whose noncommon sides are opposite rays W 3. If m⬔CSW 45, what is m⬔JST ? How do you know? complementary—two angles whose measures have a sum of 90 C K S Z 45; they are vertical angles. D J T R F vertical—two nonadjacent angles formed by two intersecting lines Angle pairs can be E 4. If m⬔FKB 135, what is m⬔BKL? How do you know? supplementary—two angles whose measures have a sum of 180° 45; the angles are supplementary. 5. Name three angles whose measures sum to 180. Sample answer: ⬔ABM, ⬔MBK, and ⬔KBC Identify each pair of angles as complementary, supplementary, linear, vertical, or adjacent. Use the graphic organizer above to help you. Keep in mind that there may be more than one answer for each exercise. Choose the best answer. 6. A landscaper uses paving stones for a walkway. Which are possible angle measures for a and b so that the stones do not have space between them? A 50, 100 C 75, 105 B 45, 45 D 90, 80 A complementary vertical 3. 4. J 180 supplementary 8. ⬔R and ⬔S are complementary. If m⬔R (7 3x) and m⬔S (2x 13), which is a true statement? A ⬔R is acute. B ⬔R is obtuse. 7. The angle formed by a tree branch and the part of the trunk above it is 68. What is the measure of the angle that is formed by the branch and the part of the trunk below it? F 22 H 158 G 112 2. 1. B linear or supplementary 5. C ⬔R and ⬔S are right angles. D m⬔S m⬔R 6. adjacent Copyright © by Holt, Rinehart and Winston. All rights reserved. 33 Copyright © by Holt, Rinehart and Winston. All rights reserved. Holt Geometry Copyright © by Holt, Rinehart and Winston. All rights reserved. 66 complementary 34 Holt Geometry Holt Geometry Name : Score : Teacher : Date : Name the relationship: complementary, linear pair, vertical, or adjacent. /_ j /_ m 1) 2) /_ n /_ a ___________ 3) ___________ 4) _ / e _ / d _ / r ___________ ___________ _ / q /_ k 5) 6) _ / g _ / t /_ c ___________ ___________ /_ f 7) 8) ___________ _ / b /_ h ___________ _ / p Math-Aids.Com Name : Score : Teacher : Date : Name the relationship: complementary, linear pair, vertical, or adjacent. /_ j /_ m 1) 2) /_ n /_ a Adjacent ___________ 3) Adjacent ___________ 4) _ / e _ / d _ / r Linear Pair ___________ Vertical ___________ _ / q /_ k 5) 6) _ / g _ / t /_ c Linear Pair ___________ Complementary ___________ /_ f 7) 8) Linear Pair ___________ _ / b /_ h Adjacent ___________ _ / p Math-Aids.Com Warm-Up On the lines below, explain how you find the measure of ABC. C D 1210 A B Remember, a great essay: - Answers the question completely E - Uses vocabulary words - Contains no statements that are not accurate/true - Describes the steps taken and why (try using the word because at least once) Warm-Up On the lines below, explain how you find the measure of C ABC. D 1210 A B Remember, a great essay: - Answers the question completely E - Uses vocabulary words - Contains no statements that are not accurate/true - Describes the steps taken and why (try using the word because at least once) CCSD Version Date: March 2012 Class Notes Example 1: C 3x0 510 A B D E What is the value of x? What is the measure of angle ABC? Show your work. Answer: degrees --------------------------------------------------------------------------------------------Example 2: C A (6x + 19)0 x0 D B E Part A What is the value of x? Show your work. Part B What is the measure of angle ABC? Show your work. Answer: degrees What are some math words we should use to explain our answer to Part B? CCSD Version Date: March 2012 Class Notes C Example 3: (2x-11)0 A 510 F D B E What is the value of x? What is the measure of angle ABF? Show your work. Answer: degrees Example 4: C 780 A B (5x –2)0 D E Part A What is the value of x? Show your work. Part B What is the measure of angle DBE? Show your work. Answer: degrees What are some math words we should use to explain our answer to Part B? CCSD Version Date: March 2012 Independent Practice 1) Write and solve an equation to find the value of x and the measure of each angle labeled. Work Space: (2x - 11) 105 X = ____________ 2) Find the value of x. Then find the measure of the unknown angle. Equation: ______________________________ 62 (x + 10) x = ________ Unknown angle = ____________ CCSD Version Date: March 2012 3) 4) D and G are supplementary angles. The measure of What is the degree measure of D ? D is 4 times the measure of 5) Solve for x. Then explain how you found the value of x. (3x + 12)° 72° CCSD Version Date: March 2012 G. 23 (4x +10)0 500 What is the value of x? 30 C A (3x +5)0 (x+15) B 0 D What is the measure of angle ABC? 125 (x+5)0 (x - 15)0 What is the value of x? 50 m 1= (x+4)0 m 2 = (5x + 8)0 What is the measure of angle 1? 17 C 0 A (3x) B (x + 8)0 D What is the measure of angle CBD? 51 (2x - 11)0 1050 What is the value of x? ______ 58 (2x + 10)° 60° What is the value of x? ______ 55 100° (4x − 8)° What is the value of x? 22 30° (5x + 10)° What is the value of x? 10 52° (3x − 1)° What is the value of x? 13 155° (5x)° What is the value of x? 5 (2x + 24)° 70° What is the value of x? ______ Name: ____________________________ Date:___________________ CITY PROJECT You will work in a group. Each group should have the following roles filled by different students: City Planner (makes up the names of streets and buildings) ___________________ Architect (builds/draws the streets and buildings) ___________________ Supplier (gathers/delegates supply list for the group) ___________________ Councilman (checks design has all requirements/appearance) ___________________ You and your group are to design your own city and include the following: 1. City name and population at the top of the project 2. Two parallel streets (each street must be named) 3. One street intersecting the two parallel streets (each street must be named) 4. One street that is perpendicular to the two parallel streets with an additional street creating complementary angles (each street must be named) The following buildings must be placed as directed: 5. The hospital and the hardware store are supplementary angles 6. Your house and school must be vertical angles 7. Courthouse and bank must be complementary angles 8. The Gas station and a Restaurant form a linear pair 9. Traffic light at two intersections or more (draw 3 circles on top of each other just like a stop light) 10. The police station and the gas station are vertical angles 11. The fire station is supplementary to the courthouse and the bank 12. Name and label each building 13. Use crayons or colored pencils to draw your city or use 3-dimensional objects. BE CREATIVE!!!!! 14. Turn in this sheet with your project CHECKLIST: ITEM Streets (named) Hospital (named) Police Station (named) Gas station (named/location) Restaurant CCSD Version Date: March 2012 POINTS POSSIBLE 5 8 8 8 8 POINTS RECIEVED (named/location) House (named/location) School (named/location) Courthouse (named/location) Bank (named/location) Hardware Store (named/location) Fire Station (named/location) Traffic lights (named/location) General appearance 8 8 8 8 8 8 5 10 A Sample Layout Fire Station House Courthouse School Bank Gas Station Restaurant Police Station CCSD Version Date: March 2012 Hardware Store Hospital