* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download File
Metric tensor wikipedia , lookup
Riemannian connection on a surface wikipedia , lookup
Golden ratio wikipedia , lookup
Rational trigonometry wikipedia , lookup
Euclidean geometry wikipedia , lookup
Integer triangle wikipedia , lookup
Perceived visual angle wikipedia , lookup
Pythagorean theorem wikipedia , lookup
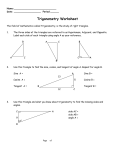
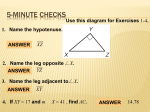
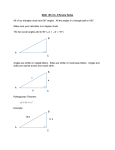
Lesson 43: Sine, Cosine, and Tangent, Inverse Functions Here we show three triangles. Each one is a right triangle, and each one contains a 30° angle. 4 2 30° 120 30° 3.464 103.92 60 240 30° 207.85 120 The longest side of a right triangle is always the side opposite the right angle, and this side is called the hypotenuse. The hypotenuses of these triangles from left to right are 4, 120, and 240 units long. We remember that right triangles that also have one equal acute angle are similar triangles and that the ratios of corresponding sides of similar triangles are equal. If for each of the three triangles shown we write the ratio of the side opposite the 30° angle to the hypotenuse, we get these expressions, each of which has a value of 0.5. 2/4 60/120 120/240 We would find this to be true for this ratio in any right triangle with a 30° angle. In a right triangle we call this ratio, which is the ratio of the side opposite the angle to the hypotenuse, the sine of the angle. sin 30° = side opposite 30° angle hypotenuse This ratio always equals 0.5 for a 30° angle. Every angle has a specific value for the ratio of the opposite side to the hypotenuse. In a right triangle the ratio of the side adjacent to the angle to the hypotenuse is called the cosine of the angle. cos 30° = side adjacent 30° angle hypotenuse We call the ratio of the side opposite the angle to the side adjacent to the angle the tangent of the angle. tan 30° = side opposite 30° side adjacent 30° SOH CAH TOA Sin = Opp. Cos = Adj. Tan = Opp. Hyp. Hyp. Adj. The sines, cosines, and tangents of angles can be obtained by using the “sin”, “cos”, and “tan” keys on a scientific calculator. To find the proper values when the angle is measured in degrees, the calculator must be in degree mode. Calculators will give an estimate of the value of a trigonometric function to more than five decimal places. To find the sine of 39.2°, firs put the calculator in degree mode (press the “deg” or “drg” key). Then enter “39.2”, then “sin”. sin 39.2° ≈ .63 Example: Find the cosine and tangent of 39.2°. Answer: Cos 39.2° ≈ .775 Tan 39.2° ≈ .816 Example: Solve 4 cos 57.2° Answer: 2.17 Example: Find the sine of A, the cosine of B and the tangent of C. Round answers to two decimal places. 7 4 8.6 A 5.74 5 6 10 B C 7 8 Answer: Sin A = 4/7 ≈ 0.57 Cos B = 7/8.6 ≈ 0.81 Tan C = 6/8 ≈ 0.75 The inverse sine of a number is the angle whose sine is the number. Several examples will help. a) The sine of 30° is 0.5, so the inverse sine of 0.5 is 30° b) The cosine of 30° is approximately 0.866, so the inverse cosine of 0.866 is 30° c) The tangent of 30° is approximately 0.577, so the inverse tangent of 0.577 is 30° To find the inverse sine, cosine and tangent of a number, we use the “inv” key followed by the trigonometric function key. Example: Find (a) the angle whose sine is 0.643 and (b) the angle whose cosine is 0.216. Answer: a) ≈ 40° b) ≈ 77.53° HW: Lesson 43 #1-30