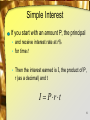* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Exponential Functions
Computational electromagnetics wikipedia , lookup
Computational fluid dynamics wikipedia , lookup
Generalized linear model wikipedia , lookup
Demographics of the world wikipedia , lookup
Theoretical ecology wikipedia , lookup
Okishio's theorem wikipedia , lookup
Time value of money wikipedia , lookup
Plateau principle wikipedia , lookup
Credit card interest wikipedia , lookup
Interest rate wikipedia , lookup
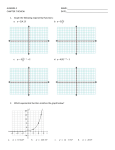
Exponential Functions Lesson 2.4 Aeronautical Controls Exponential Rate • Offers servo travel that is not directly proportional to stick travel. • Control response isWhat milderairplane below half-stick, but becomes increasing is this? stronger as stick travel approaches 100%. Great for aerobatics and trouble situations. 2 General Formula All exponential functions have the general format: f (t ) A B t Where • A = initial value • B = growth rate • t = number of time periods 3 Typical Exponential Graphs When B > 1 f (t ) A Bt When B < 1 4 Exponential Equations Given a a x y • What could you say about x and y? If the two quantities are equal and the base value for the exponential expression are the same . . . • Then the exponents must be the same Use to solve exponential equations 9 27 x 5 Simple Interest If you start with an amount P, the principal • and receive interest rate at r% • for time t • Then the interest earned is I, the product of P, r (as a decimal) and t I P r t 6 Compound Interest Consider an amount A0 of money deposited in an account • Pays annual rate of interest r percent • Compounded m times per year • Stays in the account t years Then the resulting balance At r An A0 1 m mt 7 Compound Interest What happens when we increase the number of compounding periods? Try $1000 at 3.5% for 6 years • Compounded yearly? • Quarterly • Monthly • Weekly • Daily • For every hour? every minute? every second? 8 The Irrational Number e As the number of compounding periods increase • The change in the end result becomes less • We reach a limit Can be shown r lim P 1 m m mt Pe r t • Where e ≈ 2.71828 Note Page 90, 91 9 Continuous Compounding Try our $1000 at 3.5% for 6 years using Pe Compare to r t r An A0 1 m mt with large m 10 Assignment Lesson 2.4 Page 106 Exercises 3 – 47 EOO 11