Download Modular Cell Biology: Retroactivity and Insulation

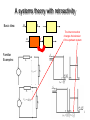
Modular Cell Biology:
Retroactivity and Insulation
Domitilla Del Vecchio
EECS, University of Michigan at Ann Arbor
MechE, MIT
Oxford, September 2009
1
Modularity: A fundamental property
Modularity guarantees that the input/output
behavior of a component (a module) does not
change upon interconnection.
Electronics and Control Systems Engineering rely
on modularity to predict the behavior of a complex
network by the behavior of the composing
subsystems.
Internal circuitry of an OPAMP:
It is composed of well defined modules
Result: Computers, Videos, cell phones…
Functional modules seem to recur also in biological
networks (e.g. Alon (2007)). But…
But can they be interconnected and still maintain their
behavior unchanged?
If not, what mechanism can be used to interconnect
modules without altering their behavior?
The Emergent integrated circuit of the cell
[Hanahan & Weinberg (2000)]
Does nature already employ such mechanisms?
2
Modularity: A grand challenge in synthetic
biology X
Z
Repressilator
(Experimental Results)
(Elowitz and Leibler, Nature 2000)
Courtesy of Elowitz Lab at Caltech
WORKING “MODULES”
NOT WORKING
INTERCONNECTIONS !
Modularity is not a natural property of
bio-molecular circuits
Experimental data
LacI-rep
NRI-act
IPTG
glnG
glnKp
lacI
(Atkinson et al, Cell 2003)
Retroactivity!
LOAD
Courtesy of Ninfa Lab at Umich
How do we model these effects? How do we prevent them?
4
Outline
• A modeling framework for systems with retroactivity
• Retroactivity in transcriptional networks
• A lesson from OPAMPs: Insulation devices
• Design of a bio-molecular insulation device based on
phosphorylation/dephosphorylation
• Fast time-scales as a key mechanism for insulation
5
A systems theory with retroactivity
Basic Idea:
y
u
u
y’
The interconnection
changes the behavior
of the upstream system
Familiar
Examples:
6
A systems theory with retroactivity
u
r
Retroactivity to the input
y
s
Retroactivity to the output
Def: The I/O model of the isolated system is obtained when s=0 and when r is
not an additional output
The interconnection of two systems is possible only when the internal state variable
sets are disjoint:
u2=y1
y1 u2
s1
r2
s1=r2
7
Outline
• A modeling framework for systems with retroactivity
• Retroactivity in transcriptional networks
• A lesson from OPAMPs: Insulation devices
• Design of a bio-molecular insulation device based on
phosphorylation/dephosphorylation
• Fast time-scales as a key mechanism for insulation
8
Gene regulatory circuitry: A network of
transcriptional modules
Z
X
A transcriptional
component is typically
viewed as an input/output
module
But, is its input/output response unchanged upon interconnection?
9
Retroactivity in transcriptional networks has
dramatic effects on the dynamics
Downstream
component
(isolated)
(connected)
s
10
Measure of the retroactivity
We seek to quantify the difference in the dynamics of the state X between
the connected and isolated system
Isolated system (1D)
Connected system
(2D)
s
To compare the X dynamics we seek a 1D approximation for the connected system:
Measure of retroactivity will be given by
11
Calculation of s
We exploit the time-scale separation between the output X dynamics and the dynamics
of the input stage of the downstream component
12
Meaning and value of
Isolated system dynamics:
Approximate connected system dynamics:
percentage difference
between the isolated system
dynamics and the approximate
connected system dynamics
The value of the retroactivity
measure for the interconnection
through transcriptional regulation
Del Vecchio et al., Nature Molecular Systems Biology 2008
13
Effect of R(X) on the dynamics
Downstream
component
(isolated)
(connected)
Retroactivity shifts the poles
of the transfer function of the
linearized system toward
low frequency
14
Outline
• A modeling framework for systems with retroactivity
• Retroactivity in transcriptional networks
• A lesson from OPAMPs: Insulation devices
• Design of a bio-molecular insulation device based on
phosphorylation/dephosphorylation
• Fast time-scales as a key mechanism for insulation
15
Dealing with retroactivity: Insulation devices
In general, we cannot design the downstream system (the load) such that it
has low retroactivity. But, we can design an insulation system to be placed
between the upstream and downstream systems.
u
r≈ 0
y
s
1. The retroactivity to the input is approx zero: r≈0
2. The retroactivity to the output s is attenuated
3. The output is proportional to the input: y=c u
16
Reaching small retroactivity to the input r
Non-inverting amplifier:
because the input stage of an OPAMP
absorbs almost zero current
Choose the biochemical parameters of the
input stage to allow a small value of
For example:
17
Dealing with retroactivity: Insulation devices
In general, we cannot design the downstream system (the load) such that it
has low retroactivity. But, we can design an insulation system to be placed
between the upstream and downstream systems.
u
r≈ 0
y
s
1. The retroactivity to the input is approx zero: r≈0
2. The retroactivity to the output s is attenuated
3. The output is proportional to the input: y=c u
18
Attenuation of the retroactivity to the output
“s”: Large feedback and large amplification
Non-inverting amplifier:
For G large enough:
Conceptually:
19
Attenuation of the retroactivity to the output
“s” in the transcriptional component
Connected system approximated dynamics
Isolated system
Apply large input amplification G and large output feedback G’
How do we realize a large input amplification and a large negative feedback?
20
Outline
• A modeling framework for systems with retroactivity
• Retroactivity in transcriptional networks
• A lesson from OPAMPs: Insulation devices
• Design of a bio-molecular insulation device based on
phosphorylation/dephosphorylation
• Fast time-scales as a key mechanism for insulation
21
A phosphorylation-based design for a biomolecular insulation device
Amplification through
phosphorylation
Phospho/Dephospho
Reactions:
Feedback through
dephosphorylation
s
Full ODE Model
r
22
Simplified analysis: Why should it attenuate
“s”?
s
Del Vecchio et al., Nature Molecular Systems Biology 2008
23
Outline
• A modeling framework for systems with retroactivity
• Retroactivity in transcriptional networks
• A lesson from OPAMPs: Insulation devices
• Design of a bio-molecular insulation device based on
phosphorylation/dephosphorylation
• Fast time-scales as a key mechanism for insulation
24
Full system: The fast time-scale of the
device is a key feature for attenuating “s”
Phosphorylation and dephosphorylation reactions are often much faster than
protein production and decay:
25
Fast time scales: A key mechanism for
insulation
Basic Idea:
Large
Interconnection
through binding/unbinding
(possibly large)
Claim: if G is large enough, signal x at the QSS is not affected by y.
26
Fast time scales: A key mechanism for
insulation
Why would it work?
x(t) does not depend on y on the slow
manifold
Del Vecchio and Jayanthi, CDC 2008
27
Simulation results for the pho/depho
insulation device
Slow time-scale
Fast time-scale
The fast time-scale of the
phosphorylation cycle allows
to reach insensitivity to very
large loads (p=100)
Xp for the isolated system
Xp for the connected system
28
Conclusions
We have proposed a systems theory with retroactivity
We have provided a measure of retroactivity in transcriptional
networks
We have introduced the notion of insulation device
r=0
We have presented a general (very well known in control systems
engineering) mechanism to attenuate retroactivity to the output
Futile cycles, which are ubiquitous in natural signal
transduction systems are excellent insulation device:
they use time-scale separation as an insulation mechanism
29
Thanks to:
•
Alexander J. Ninfa (University of Michigan Medical School, Prof. of
Biological Chemistry)
•
Eduardo D. Sontag (Rutgers University, Prof. of Mathematics)
•
Sofia Merajver (University of Michigan Medical School, Cancer Center,
Medical Doctor)
•
•
•
•
Shridhar Jayanthi (EE: Systems, University of Michigan, graduate student)
Hamid Ossareh (EE: Systems, University of Michigan, graduate student)
Prasanna Varadarajan (ME, University of Michigan, graduate student)
Polina Mlynarzh (BME, University of Michigan, graduate student)
•
Rackham Graduate School at University of Michigan/ CCMB/AFOSR
30
High gains improve signal-to-noise ratio…
Bio-molecular processes are intrinsically stochastic
How do high gains (required for retroactivity
attenuation) impact noise?
Courtesy of Elowitz lab (Caltech)
Downstream
component
calculated by linearizing the system
about its equilibrium corresponding to
calculated the Fokker-Planck Equation
deriving from the Master Equation
31
…but they also increase intrinsic noise at
higher frequency
Downstream
component
Use linearized Langevin approximation
32
Jayanthi and Del Vecchio, CDC 2009
The parts of the insulation device can be
designed so as to have small “r”
Retroactivity r after a fast transient
is small if:
Approx linear input/output relationship:
Resulting input/output gain
33
Ongoing and Future Work
Experimental demonstration of genetic retroactivity in living cells
(with Shridhar Jayanthi (EECS) and Alexander J Ninfa (Med School) at Umich)
Periodic and step injection routines
IPTG
LacI
repressor
lac
promoter
lacZ lacY
lacA
LacI binding sites
(lacOp operators)
34
Ongoing and Future Work
Construction of a phosphorylation-based insulation device
(with Shridhar Jayanthi (EECS) and Alexander J Ninfa (Med School) at Umich)
IPTG
Output
Lac Repressor
kinase (NRII L16R)
lac
promoter
glnK
promoter
NRI
NRI~P
RFP
lacZ
NRI~P binding sites
(enhancers)
phosphatase
Amplifier/Insulator (NRII H139N)
35
Ongoing and Future Work
Computation of a retroactivity measure in signaling pathways and of the
“dampening” factor across stages
(with Alejandra Ventura and Sofia Merajver in the Cancer Center at Umich)
Upstream
Effect
Downstream
Perturbation
Does nature uses insulation devices by accident?
Can we show that some natural systems would not work they way they work
if the phosphorylation/dephosphorylation signaling cascades did not enjoy
insulation properties?
How general/descriptive is the system modeling with retroactivity?
(with Eduardo D. Sontag at Rutgers)
36
Higher gains may contribute to higher
biological noise
Faster phosphorylation and
dephosphorylation reactions lead to higher
amplification and feedback gains (“higher
OPAMP amplification”), which lead to higher
coefficient of variation.
37
Effect of R(X) on the dynamics
Downstream
component
(isolated)
(connected)
Retroactivity shifts the poles
of the transfer function of the
linearized system toward
low frequency
38