Download Ch 5 Inverse, Exponential and Logarithmic Functions

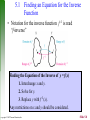
Copyright © 2007 Pearson Education, Inc.
Slide 5-1
Chapter 5: Inverse, Exponential and
Logarithmic Functions
5.1
5.2
5.3
5.4
5.5
Inverse Functions
Exponential Functions
Logarithms and Their Properties
Logarithmic Functions
Exponential and Logarithmic Equations and
Inequalities
5.6 Further Applications and Modeling with
Exponential and Logarithmic Functions
Copyright © 2007 Pearson Education, Inc.
Slide 5-2
5.1 Inverse Functions
1
Example Let f ( x)  8 x and g ( x)  x.
8
f (12)  8  12  96
1
g (96)   96  12
i.e. g[ f (12)]  12
8
Also, f [g(12)] = 12. For these functions, it can be
shown that
f [ g ( x)]  x and g[ f ( x)]  x
for any value of x. These functions are inverse functions
of each other.
Copyright © 2007 Pearson Education, Inc.
Slide 5-3
5.1 One-to-One Functions
A function f is a one-to-one function if, for
elements a and b from the domain of f,
ab
•
implies
f (a)  f (b).
Only functions that are one-to-one have
inverses.
Copyright © 2007 Pearson Education, Inc.
Slide 5-4
5.1 One-to-One Functions
Example Decide whether the function is one-to-one.
(a) f ( x)  4 x  12
(b) f ( x)  25  x 2
Solution
(a) For this function, two different x-values produce
two different y-values.
Suppose that a  b, then  4a  4b and
 4a  12  4b  12. Since f (a )  f (b), f is one - to - one.
(b) If we choose a = 3 and b = –3, then 3  –3, but
f (3)  25  32  4 and f (3)  25  (3) 2  4,
so f (3)  f (3), therefore f is not one - to - one.
Copyright © 2007 Pearson Education, Inc.
Slide 5-5
5.1 The Horizontal Line Test
If every horizontal line intersects the graph of a
function at no more than one point, then the function
is one-to-one.
Example Use the horizontal line test to determine
whether the graphs are graphs of one-to-one functions.
(a)
(b)
Not one-to-one
Copyright © 2007 Pearson Education, Inc.
One-to-one
Slide 5-6
5.1 Inverse Functions
Let f be a one-to-one function. Then, g is the
inverse function of f and f is the inverse of g if
( f  g )( x)  x for every x in the domain of g ,
and
( g  f )( x)  x for every x in the domain of f .
Example Show that f ( x)  x3  1 and g ( x)  3 x  1
are inverse functions of each other.
( f  g )( x)  f [ g ( x)]   x  1  1  x  1  1  x
3
3
( g  f )( x)  g[ f ( x)]  3 x3  1  1  3 x3  x
Copyright © 2007 Pearson Education, Inc.
Slide 5-7
5.1 Finding an Equation for the Inverse
Function
• Notation for the inverse function f -1 is read
“f-inverse”
Finding the Equation of the Inverse of y = f(x)
1. Interchange x and y.
2. Solve for y.
3. Replace y with f -1(x).
Any restrictions on x and y should be considered.
Copyright © 2007 Pearson Education, Inc.
Slide 5-8
5.1 Example of Finding f -1(x)
Example Find the inverse, if it exists, of
4x  6
f ( x) 
.
5
4x  6
Write f (x) = y.
y
Solution
5
4y  6
Interchange x and y.
x
5
Solve for y.
5x  4 y  6
5x  6
y
4
5x  6
1
Replace y with f -1(x).
f ( x) 
4
Copyright © 2007 Pearson Education, Inc.
Slide 5-9
5.1 The Graph of f -1(x)
• f and f -1(x) are inverse functions, and f (a) = b for
real numbers a and b. Then f -1(b) = a.
• If the point (a,b) is on the graph of f, then the point
(b,a) is on the graph of f -1.
If a function is one-to-one,
the graph of its inverse f -1(x)
is a reflection of the graph of
f across the line y = x.
Copyright © 2007 Pearson Education, Inc.
Slide 5-10
5.1 Finding the Inverse of a Function
with a Restricted Domain
Example
Let f ( x)  x  5. Find f 1 ( x).
Solution
Notice that the domain of f is restricted
to [–5,), and its range is [0, ). It is one-to-one and
thus has an inverse.
y  x5
x  y5
x2  y  5
2
y  x 5
The range of f is the domain of f -1, so its inverse is
f 1 ( x)  x 2  5, x  0.
Copyright © 2007 Pearson Education, Inc.
Slide 5-11
5.1 Important Facts About Inverses
1. If f is one-to-one, then f -1 exists.
2. The domain of f is the range of f -1, and the
range of f is the domain of f -1.
3. If the point (a,b) is on the graph of f, then the
point (b,a) is on the graph of f -1, so the graphs
of f and f -1 are reflections of each other
across the line y = x.
Copyright © 2007 Pearson Education, Inc.
Slide 5-12
5.1 Application of Inverse Functions
Example Use the one-to-one function f(x) = 3x + 1 and the
numerical values in the table to code the message BE VERY
CAREFUL.
A 1
F 6
K 11
P 16
U 21
B 2
G 7
L 12
Q 17
V 22
C 3
H 8
M 13
R 18
W 23
D 4
I 9
N 14
S 19
X 24
E 5
J 10
O 15
T 20
Y 25
Z 26
Solution BE VERY CAREFUL would be encoded as
7 16 67 16 55 76 10 4 55 16 19 64 37
because B corresponds to 2, and f(2) = 3(2) + 1 = 7,
and so on.
Copyright © 2007 Pearson Education, Inc.
Slide 5-13