* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Properties of Light
Survey
Document related concepts
Gravitational wave wikipedia , lookup
Circular dichroism wikipedia , lookup
Health threat from cosmic rays wikipedia , lookup
Microplasma wikipedia , lookup
Photon polarization wikipedia , lookup
First observation of gravitational waves wikipedia , lookup
Transcript
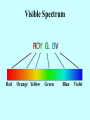
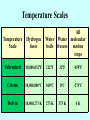
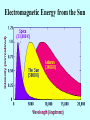
Radiation Information from the Cosmos Radiation,Waves, & Information • Most of the information around us gets to us in waves. • Sound energy that travels to our ears is in one form of wave. • Light is energy that comes to our eyes if the form of another type of wave. • Energy (information) that is transferred from place to place in the form of a wave is called RADIATION. Information from the Cosmos • Until recently, our knowledge of the universe was obtained only by studying the visible light that happened to arrive on Earth. • Since the 1930’s, possible to study other types of radiation and particles --– radio waves, X-rays, gamma rays, cosmic rays, neutrinos, and gravitational radiation. • To understand the methods used to study the cosmos, we must understand the basic nature and behavior of light. So, what is light? • The particle or ray model of light is illustrated by the properties of reflection and refraction. • The wave model of light is illustrated by the properties of reflection, refraction, diffraction, interference, and polarization. • But there are problems: if light is a wave, and waves need a “medium” such as air or water to carry them, then how can light travel through empty space? • The solution was to decide that light was neither a wave nor a particle, but something else which sometimes behaved like them. Is it a particle? Is it a wave? It is neither, but it’s like both What is a Wave? • Wave motion is NOT a mechanical phenomenon because a wave is not a material object but a form. – It cannot be assigned a mass, and the concept of acceleration cannot be applied to a wave. – The motion of a wave is vastly different from the motion of the medium in which it travels. In fact, a wave can exist without any movement of matter at all! • So, what is a wave? It is a pattern or form that moves. • It can be a – deformation of a material object (music string or waves on the surface of a body of water) OR – pattern in a field (light or radio waves). Waves: Standard Dimensions In physics, waves are described by a few standard dimensions. Wavelength = length of one cycle Amplitude A= height of wave above “rest position” Frequency f = how often wave crest passes, longer wavelength means lower frequency Velocity v= speed of wave v=f x Frequency and Period Frequency: how often a vibration (cycle, repetition) occurs in some interval of time, # vibrations (or cycles) per unit time. units are Hertz (Hz) 1-Hz = 1 vibration/sec = 1 cycle/sec 103 Hz = kHz (AM radio frequencies) 106 Hz = MHz (FM radio frequencies) Period: the time to complete one vibration (or cycle), the inverse of the frequency period = 1 / frequency OR frequency = 1 / period Wave Speed • The speed of some waves depends on the medium through which the wave travels. – Sound waves travel at speeds of 330 - 350 m/s in air, and about four times as fast in water. • The speed of the wave is related to the frequency and wavelength of the wave. Wave speed = frequency x wavelength Motion of Waves Is there a relationship between the motion of the wave through space and the motion of the medium that a wave moves in? Wave Types • Two types of waves –transverse –longitudinal Cheerleader demo Types of waves Transverse waves: the motion of the medium is at right angles to the direction in which the wave travels. Examples: stretched strings of musical instruments, waves on the surfaces of liquids, some of the waves produced in earthquakes. Although they require no “medium” to travel, electromagnetic waves are also transverse waves. Longitudinal waves: the particles in the medium move along the direction of the wave; travel in solids, liquids, and gases. Examples: sound waves, some of the waves produced in earthquakes. Do waves travel through empty space? What if there is no medium to move in? Can any waves travel through empty space? If so, which ones? Light as a Wave • Light is a type of radiation; it is a type of wave that travels through space. • Light waves are fundamentally different from many other waves that travel only through material media (sound or water waves). • Light waves require NO material medium to travel from place to place. • The wave speed of all types of light in a vacuum is called the speed of light, c. c = 300,000 km/sec Terminology • Radiation: a way to transfer of energy in the form of a wave • Light: another name for electromagnetic radiation • Electromagnetic (EM) radiation: Also known as light, transfers energy and information from one place to another (in form of coupled electric and magnetic waves) • Visible light: the range of electromagnetic radiation that the human eyes perceive as visible Group Question 1. Determine the wavelength of your group’s favorite radio station. 2. Assume you are 100 km (~60 miles) from the station transmitter. Calculate how long it takes for the radio waves to arrive at your location from the radio station transmitter. Wave speed = frequency x wavelength Speed of light (radio waves) = c = 3x 108m/sec Distance = speed x time x103 Hz (AM radio frequencies) x106 Hz (FM radio frequencies) Creating Electromagnetic Waves •All matter is made up of atoms. •Atoms are, in turn, made up of smaller particles: protons, electrons, and neutrons. •Two of the elementary particles that make up atoms possess a property described as electrical charge. •The charges on each are equal and opposite. electron: - charge proton: + charge Charged Particle Interactions Any electrically charged object exerts a force on other charged objects. Electrons negatively charged Protons positively charged Like charges repel one another. Unlike charges attract. Electrical Force • Electrical force: – is a universal force (every charged particle affects every other charged particle) – may be attractive or repulsive force – is always directed along the line connecting two charges – depends on the product of the two charges – depends on the distance between the two charges squared • (obeys the “inverse square rule”) • Today, physicists describe electric forces in terms of an electrical field produced by the presence of electrical charge. Charged Particles and Electric Fields Electric field strength An electric field extends outward in all directions from any positively charged particle. If a charged particle moves, its electric field changes. The resulting disturbance travels through space as a wave. proportional to 1/r2 . Magnetic Fields • If an electric field changes with time (let’s say the source charge wiggles), then a magnetic field is created, coupled to the time-variant electric field. • Magnetic fields influence behavior of magnetized objects. – Earth’s magnetic field causes compass needles to point N – bar magnets – electromagnets Electromagnetism Electric and magnetic fields do not exist as independent entities. They are different aspects of a single phenomenon: Electromagnetism (EMR) Together, they constitute an electromagnetic wave that carries energy and information from one part of the universe to another. Frequency and Energy Light waves carry energy (E) across space. The energy is related to the frequency of the light wave by E = hf where h = Planck’s constant Recall that wave speed relates frequency and wavelength: v = f and for light, so, E f c = f or E 1/ Creating and Detecting Light • Light is created by the motion of charged particles. • Matter is made up of atoms, which are in turn made up of charged particles. • Motions of these charged particles create light. – Not just the light we detect with our eyes, but at all wavelengths (or frequencies). Electromagnetic Spectrum Properties of Light • • • • • • Polarization Reflection Refraction Dispersion Diffraction Interference Properties of Light: Reflection and Refraction • An isolated light beam travels in a straight line. • Light can change directions under certain conditions: • Reflection from a surface, – mirrors, objects • Refraction (or bending of a ray of light) as the ray travels from one transparent medium to another. – pencil in a clear glass of water – light through a piece of glass Properties of Light: Dispersion •Electromagnetic waves interact with the charged particles in matter and travel more slowly in transparent media than in a vacuum. •The change in speed of the light wave causes the wave to refract. •Since the speed of an EM wave in a medium changes with wavelength, the amount of refraction depends on the wavelength. •This effect is called dispersion. Visible Light • Prism will separate light into its components • Composed of 7 hues (Roy G. Biv), known as its spectrum – – – – – – – Red (~ 700 nm or 7000 Å) Orange Yellow Green Blue Indigo Violet (~ 400 nm or 4000 Å) • Color determined by its frequency (or, equivalently, its wavelength) Visible Spectrum Red Orange Yellow Green Blue Violet Properties of Light: Diffraction • Diffraction is the bending of a wave as it passes through a hole or around an obstacle. – If light consists of parallel rays, they would travel through a small pinhole and make a small, bright spot on a nearby screen. Sharp-edged shadow Fuzzy shadow Effect cannot be explained by ray model of light. Diffraction of Waves • Actually observe a spot larger than the pinhole and varying in brightness. – The pinhole somehow affects the light that passes through it. • Diffraction is proportional to the ratio of wavelength to width of gap. – The longer the wavelength and/or the smaller the gap, the greater the angle through which the wave is diffracted. Fuzzy shadow Properties of Light: Interference and Superposition • What happens if two waves run into each other? • Waves can interact and combine with each other, resulting in a composite form. • Interference is the interaction of the two waves. – reinforcing interaction = constructive interference – canceling interaction = destructive interference • Superposition is the method used to model the composite form of the resulting wave. Interference of Waves Interference: ability of two or more waves to reinforce or cancel each other. Constructive interference occurs when two wave motions reinforce each other, resulting in a wave of greater amplitude. Destructive interference occurs when two waves exactly cancel, so that no net motion remains. Radiation and Temperature • What determines the type of electromagnetic radiation emitted by the Sun, stars, and other astronomical objects? Temperature • Electromagnetic radiation is emitted when electric charges accelerate, changing either the speed or the direction of their motion. • The hotter the object, the faster the atoms move in the object, jostling one another, colliding with more electrons, changing their motions with each collision. • Each collision results in the emission of electromagnetic radiation- radio, infrared, visible, ultraviolet, x-rays. How much of each depends on the temperature of the object producing the radiation. Measuring Temperature • Atoms and molecules that make up matter are in constant random motion. • Temperature is a direct measure of this internal motion. – The higher the temperature, the faster (on average) the random motion of particles in matter. – Temperature of an object represents the average thermal energy of particles that make up that object. TWO MAJOR SCALES °F and °C • Fahrenheit scale based on temperature that salt water freezes 0°F (lower than pure water). • Related to Celsius (or Centigrade) by the formula: F = 9/5 C + 32 C = 5/9(F - 32). ABSOLUTE SCALE K AND °C • Celsius (originally Centigrade) based on freezing and boiling point of pure water, chosen to be 0°C and 100°C • Kelvin based on absolute coldest temperature possible (absolute zero) • Related by K = C – 273.15 C = K + 273.15 Temperature Scales All Water Water molecular boils freezes motion stops Temperature Scale Hydrogen fuses Fahrenheit 18,000,032oF 212oF 32oF -459oF Celsius 10,000,000oC 100oC 0oC -273oC Kelvin 10,000,273 K 273 K 373 K 0K Radiation Laws • Blackbody Radiation – Planck Spectrum – Characteristics of Radiator • Wien’s Law – Relates wavelength at which a blackbody emits its maximum energy, max, to the temperature, T, of the blackbody. • Stefan-Boltzmann Law – Relates total energy emitted per second per square meter by a blackbody, E, to the 4th power of its absolute temperature T. Blackbody Radiation • Consider an idealized object that absorbs all the electromagnetic radiation that falls on it - called a “blackbody.” • A blackbody absorbs all energy incident on it and heats up until it is emitting energy at the same rate that it absorbs energy. • The equilibrium temperature reached is a function of the total energy striking the blackbody each second. Characteristics of Blackbody Radiation • A blackbody with a temperature higher than absolute zero emits some energy at all frequencies (or wavelengths). • A blackbody at higher temperature emits more energy at all frequencies (or wavelengths) than does a cooler one. • The higher the temperature of a blackbody, the higher the frequency (the shorter the wavelength) at which the maximum energy is emitted. Blackbody Radiation • Blackbody radiation: the distribution of radiation emitted by any heated object. • The curve peaks at a single, well-defined frequency and falls off to lesser values above and below that frequency. The overall shape (intensity vs frequency) is characteristic of the radiation emitted by any object, regardless of its size, shape, composition, or temperature. Planck Spectrum • As an object is heated, the radiation it emits peaks at higher and higher frequencies. • Shown here are curves corresponding to temperatures of 300 K (room temperature), 1000 K (glow dull red), 4000 K (red hot), and 7000 K (white hot). “Red Hot” • As something begins to heat-up, there probably isn’t any visible information to tell you it is warming up. • Once it starts to glow red, you have learned it’s hot – don’t touch. – Like the stove burners. • As it continues getting hotter, it changes to orange, then yellow, green, blue and white. Wien’s Law • The Sun and stars emit energy that approximates the energy from a blackbody. • It is possible to estimate their temperatures by measuring the energy they emit as a function of wavelength - that is, by measuring their color. • The wavelength at which a blackbody emits its maximum energy can be calculated by max = 3,000,000 / T where the wavelength max is in nanometers (10-9 m) and the temperature T is in kelvin. • This relationship is known as Wien’s law. Effect of Temperature Hotter objects are brighter and “bluer” than cooler objects. Getting Warmer Electromagnetic Radiation Type of Radiation Wavelength Range (nm) Radiated by Objects at this Temperature Typical Sources Gamma rays Less than 0.01 More than 108 K X rays 0.01 – 20 106 – 107 K Ultraviolet 20-400 105 – 106 K Visible 400-700 103 – 105 K No astronomical sources this hot; some produced in nuclear reactions. Gas in clusters of galaxies; supernova remnants; solar corona. Supernova remnants; very hot stars. Stars Infrared 103 – 106 10 – 103 K Radio More than 106 Less than 1 K Cool clouds of dust and gas, planets, satellites No astronomical objects this cold: radio emission produced by electrons moving in magnetic fields Problem - Wien’s law • The average surface temperature of the Sun is about 5800 K. At what wavelength is maximum energy emitted from the Sun? • If T = 5800 K • and max = 3,000,000 / T , • then max = 3,000,000 / 5800 = 520 nm. • 520 nm is at the middle of the visible light portion of the electromagnetic spectrum. • The human eye is most sensitive to the wavelengths at which the Sun puts out the most energy. Stefan-Boltzmann Law • If add up the contributions from all parts of the E-M spectrum, obtain the total energy emitted by a blackbody over all wavelengths. • That total energy emitted per second per square meter by a blackbody at temperature T is proportional to the 4th power of its absolute temperature. • This is known as the Stefan-Boltzmann law, E = T4 where E stands for the total energy and is a constant number. Problem - Stefan-Boltzmann Law ET = T4 • E2T = (2T)4 •The average surface temperature of the Sun • = (2)4 T4 is about 5800 K. 4 ( T4 ) • = (2) If the Sun were twice as hot, 2 T = 2 x 5800 K • = 16 ( T4 ) = 11,600 K, • = 16 ET how much more energy would it radiate than it The energy radiated by the does now? Sun would be 24 or 16 times more than now. Electromagnetic Spectrum Electromagnetic Energy from the Sun Why Do We Need Space Telescopes? Opacity of the Atmosphere Half-Absorption Altitude (km) • Only a small fraction of the radiation produced by astronomical objects actually reaches our eyes because atoms and molecules in the Earth's atmosphere absorb certain wavelengths and transmit others. • Opacity is proportional to the amount of radiation that is absorbed by the atmosphere. Wavelength (angstroms)