Download Sequential Circuit

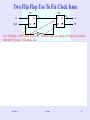
CS 3501 - Chapter 3 (3A and 10.2.2)
Part 6 of 8
Dr. Clincy
Professor of CS
• Exam 1 Review Today
• Exam 2 Part 1 on Thursday (closed book)
Dr. Clincy
Lecture
Slide 1
Half Adder Combinational Circuits
• Combinational logic circuits
give us many useful devices.
• One of the simplest is the
half adder, which finds the
sum of two bits.
• We can gain some insight as
to the construction of a half
adder by looking at its truth
table, shown at the right.
Dr. Clincy
Lecture
2
Full Adder Combinational Circuits
• We can change our half
adder into to a full adder
by including gates for
processing the carry bit.
• The truth table for a full
adder is shown at the
right.
Dr. Clincy
Lecture
3
Adders - Combinational
Circuits
• Just as we combined half adders to make a full
adder, full adders can be connected in series.
• The carry bit “ripples” from one adder to the next;
hence, this configuration is called a ripple-carry
adder.
Today’s systems employ more efficient adders.
Dr. Clincy
Lecture
4
Decoder - Combinational Circuits
•
•
Among other things, they are useful in selecting a memory location
according to a binary value placed on the address lines of a memory bus.
This is what a 2-to-4 decoder looks like on the inside.
If x = 0 and y = 1,
which output line
is enabled?
Output - Decoded
message
Input - Encoded
message
Dr. Clincy
Lecture
5
Decoder – another example
Dr. Clincy
Lecture
6
Multiplexer - Combinational Circuits
• A multiplexer does just the opposite of a decoder.
• It selects a single output from several inputs.
• This is what a 4-to-1 multiplexer looks like on the inside.
Depending
the “select
input”
combination,
1 of 4 data
inputs is
chosen for
output
Dr. Clincy
Lecture
If S0 = 1 and S1 = 0,
which input is
transferred to the
7
output?
0
1
1
1
1
1
0
0
1
1
1
0
1
0
1
1
1
1
1
0
0
x3
1
MUX
0
1
1
0
1
1
1
x3
x3
f
x3
Multiplexer - Combinational Circuits
x1
x2
Figure A.39. Multiplexer implementation of a logic function.
Can also use multiplexers to
implement logic functions
Given this truth table, group X1,X2
being 00, 01, 10 and 11 – notice
what happens with X3
• 3-input truth table can be done
with a 4-input mux
• 4-input truth table can be done
with a 8-input mux
• 5-input truth table can be done
with a 16-input mux
• Etc..
Dr. Clincy
Also explain how the Mux is used to implement
data comm’s FDM and TDM
Lecture
8
10.2.2 - Programmable Logic Devices (PLD)
All possible
combinations
of inputs
ANDed






•••
All possible
combinations
of ANDed
inputs ORed






Re-explain Sums of Products and relationship to PLDs
Dr. Clincy
Lecture
9
10.2.2 - Programmable Logic Array (PLA)
Ability to program a PLD, is called a PLA
Dr. Clincy
Lecture
10
10.2.2 - Programmable Array Logic (PAL)
For a PLA, both the AND
array and OR array are
programmable
For a PAL, the AND array is
programmable and the OR
array is fixed
Dr. Clincy
Lecture
11
I/O block
PAL-lik e
block
I/O block
PAL-lik e
block
10.2.2 - Complex Programmable Logic Devices
(CPLDs)
PAL-lik e
block
PAL-lik e
block
I/O block
I/O block
Interconnection wires
Figure A.45. Structure of a comple
x programmable logicvice
de (CPLD).
CPLDs are comprised of 2 or
more PALs
Dr. Clincy
Lecture
12
I/O block
I/O block
I/O block
10.2.2 - Field Programmable Gate Arrays
(FPGAs)
I/O block
Logic block
Interconnection switch
Figure A.46. A conceptual block diagram of an FPGA.
PAL chips are somewhat
limited in size due to the fact
they have output pins for each
sum-of-product circuit
FPGA overcome this size
limitation by using a general
interconnection.
General interconnection
PAL
Dr. Clincy
Lecture
13
CS 3501 - Chapter 3 (3A and 10.2.2)
Part 7 of 8
Dr. Clincy
Professor of CS
Dr. Clincy
Lecture
Slide 14
Sequential Circuits Vs Combinational Circuits
New Input
Current
State or
Output
Current State or output
of the device is
affected by the
previous states
Flip Flops
Previous
State or
Output
Circuit
Sequential Logic
Previous
State or
Output
New Input
Dr. Clincy
Circuit
Combinatorial or Combinational Logic
Current
State or
Output
Current State or output
of the device is only
affected by the current
inputs
Lecture
15
NOTE
Your book doesn’t do a good job in
showing you how to derive or design
sequential circuits (using state and state
assignment tables) – the lecture will do
so – please pay close attention to the
lecture in understanding how to derive
sequential circuits.
Dr. Clincy
Lecture
Slide 16
Clock - Sequential Circuits
• State changes are controlled by clocks (clock ticks).
• Circuits can change state on the rising edge, falling
edge, or when the clock pulse reaches its highest
voltage – edge triggered.
• Level-triggered circuits change state when the clock
voltage reaches its highest or lowest level.
Dr. Clincy
Lecture
17
Current
State or
Output
S and R stand for set and reset respectively
constructed from a pair of cross-coupled
NOR gates
the stored bit is present on the output
marked Qa
If S and R inputs are both low, maintains
the Qa and Qb in constant state,
If S (Set) is pulsed high while R is held
low, then the Qa output is forced high,and
stays high even after S returns low;
if R (Reset) is pulsed high while S is held
Dr. Clincy
low, then
the Qa output is forced low, and
stays low even after R returns low.
New Input
•
•
•
•
•
•
Notice how the output feeds
the input
Flip Flops
Previous
State or
Output
Circuit
Flip Flops - Sequential Circuits
Previous
State or
Output
Lecture
Think of: Given R=0 and Qa=0,
what can this be ?
18
Gated SR Latch or Flip Flop
• The time at which the latch
is SET or RESET is
controlled by a CLOCK
input
• Called Gated SR Latch
Dr. Clincy
Lecture
19
Gated D Latch
• Inputs S and R are derived
from a single input D
• Clock pulse controls when
the output is triggered
• Samples the D input at the
time the clock is HIGH and
stores that info until the
next clock pulse
Dr. Clincy
During the time the clock is high, the
input changed, causing the output to Lecture
change – this is the problem
20
Potential Problem
• Thus far, the assumption
has been the inputs S and R
(or D) not changing while
CLK is HIGH
• What would happen if S, R
and/or D changed ? The
output would change
immediately
• This could be a problem
• To fix this (next ppt)
Dr. Clincy
During the time the clock is high, the
input changed, causing the output to Lecture
change – this is the problem
21
Two Flip Flop Use To Fix Clock Issue
FF1
D
Clock
FF2
D
Q
Clk
Q
Qm
D
Q
Clk
Q
Qs
Q
Q
Use 2 D flip flops – the FF2 clock is set to zero – therefore, if there was a change in FF1 input, D, it wouldn’t
effect the FF2 Q value – FF2 holds the value
(a) Circuit
Clock
D
Qm
Q = Qs
Clock’s negative edge causes change
(b) Timing diagram
D
The arrow only symbolizes “positive
edge” clock - the arrow with the NOT
symbolizes “negative edge” clock
Q
Q
(c) Graphical symbol
Dr. Clincy
Lecture
• If D changes while FF1 CLK is
HIGH, Qm changes immediately Qs stays the same because FF2
CLK=0
• Once the CLK goes LOW, FF2
reacts because its CLK=1 – so it
thens reflects D
22
T Flip Flop
T Flip Flops are good for
counters – changes its
state every clock cycle, if
the input, T, is 1
• Positive-edge triggered flip flop
• Since the previous state of Q was 0,
it complements it to 1
Dr. Clincy
Lecture
23
JK Flip Flop
Combines the behavior of
the SR and T flip flops
• First three entries are the same
behavior as the SR Latch (when
CLK=1)
• Usually the state S=R=1 undefined
– for the JK Flip Flop, for J=K=1,
next state is the complement of the
present state
Can store data like a D Flip Flop or can tie J & K inputs together and use to build counters (like a T flip flop)
Dr. Clincy
Lecture
24
Registers and Shift Registers
A Flip Flop can store ONE bit – in being able to handle a WORD, you will need a number
of flip flops (32, 64, etc) arranged in a common structure called a REGISTER.
• All flip flops are synchronized by a common clock
• Data written into (loaded) flip flops at the same time
• Data is read from all flip flops at the same time
F1
F2
F3
In
Clock
D
Q
Q
D
Q
D
Q
Q
Q
F4
D
Q
Out
Q
A simple shift register.
• Want the ability to rotate and shift the data
• Clock pulse will cause the contents of F1, F2, F3 and F4 to shift right (serially)
• To do a rotation, simply connect OUT to IN
Dr. Clincy
Lecture
25
Registers and Shift Registers
• Can load either serially or in parallel
• When clock pulse occurs,
• Serial shift takes place if Shift’/Load=0 or
• if Shift’/Load=1, parallel load is performed
Dr. Clincy
Lecture
26
Counters
1
T
Clock
Q
T
Q
• 3-stage or 3-bit counter constructed
using T Flip Flops
• With T Flip Flips, when input T=1, the
flip flop toggles – changes state for
each successive clock pulse
• Initially all set to 0
• When clock pulse, Q0=1, therefore
Q’=0 disabling Q1 and Q1 disables Q2
(have 1,0,0)
• For the 2nd clock pulse, Q0=0, therefore
Q’=1, causing Q1=1 and therefore
Q’=0 disabling Q2 (have 0,1,0)
• For the 3rd clock pulse, Q0=1, therefore
Q’=0 disabling Q2 and therefore
disabling Q3 (have 1,1,0)
• Etc….
Q
T
Q
Q0
Q
Q
Q1
Q2
(a) Circuit
Clock
Q0
Q1
Q2
Count
0
1
2
3
4
5
6
7
0
(b) Timing diagram
Figure A.35. A 3-bit up-counter.
LSB
000
001
Hmmm
010
011
100
Dr. Clincy 101
110
111
Lecture
27
Called a Ripple Counter
CS 3501 - Chapter 3 (3A and 10.2.2)
Part 8 of 8
Dr. Clincy
Professor of CS
Dr. Clincy
Lecture
Slide 28
NOTE
Your book doesn’t do a good job in showing you how
to derive or design sequential circuits (using state
and state assignment tables) – the lecture will do so –
please pay close attention to the lecture in
understanding how to derive sequential circuits.
You can print out the slides in this lecture only for
the next exam. You should NOT add any notes to the
printed slides. You will receive a penalty if personal
notes are written on the slides
Dr. Clincy
Lecture
Slide 29
Circuit
Recall
Combinatorial or Combinational Logic
New Input
Current State or output
of the device is only
affected by the current
inputs
Current
State or
Output
New Input
Dr. Clincy
Current
State or
Output
Current State or output
of the device is
affected by the
previous states
Flip Flops
Previous
State or
Output
Circuit
Sequential Logic
Examples:
Decoders
Multiplexers
Previous
State or
Output
Lecture
Examples:
Shift Registers
Counters 30
Sequential Circuit – State Diagram
If at 0 and x=0,
count up to 1 (and
z=0)
If x=0, count up,
x=0  z=0
If x=1, count down
S0
If at 0 and x=1,
count down to 3
(and z=0)
S1
Interested when 2
is realized – z=1
when reach 2, else
z=0
x=1  z=0
x = 1  z= 0
x = 0  z= 0
x=0  z=0
x = 1  z= 1
x=1  z=0
S3
S2
x = 0 z = 1
State diagram of a mod-4 up/down counter
that detects the count of 2.
Dr. Clincy
Lecture
State diagram
describes the
functional
behavior without
any reference to
implementation31
S1
S2
S0
0
0
S2
S3
S1
1
1
S3
S0
S2
0
0
Figure A.48. State table for the example of the up/down counter.
Sequential Circuit – State Table
Can represent the
info in the state
diagram in a state
table
x=0 z=0
S
0
S1
x=1  z=0
x=1 z=0
x=0 z=0
x=0 z=0
x=1 z=1
Present
state
x=1  z=0
S3
x=0 z=1
Next state
Outputz
x =0
x= 1
x=0
x= 1
y2 y1
Y2 Y1
Y2 Y1
0 0
0 1
1 1
0
0
0 1
1 0
0 0
0
0
1 0
1 1
0 1
1
1
1 1
0 0
1 0
0
0
Figure A.49. State assignment for the
xample
e
in Figure A.48.
S
2
State diagram of a mod-4
up/down counter that detects
the count of 2.
Dr. Clincy
Lecture
32
Sequential Circuit – Equation
Present
state
Next state
Inputs – y2,y1,x
Outputz
x =0
x= 1
x=0
x= 1
y2 y1
Y2 Y1
Y2 Y1
0 0
0 1
1 1
0
0
0 1
1 0
0 0
0
0
1 0
1 1
0 1
1
1
1 1
0 0
1 0
0
0
Figure A.49. State assignment for the
xample
e
in Figure A.48.
Outputs –Y2, Y1
Dr. Clincy
Lecture
33
Sequential Circuit – Circuit Design
D Flip Flops used
to store values of
the two state
variables between
clock pulses
Output from Flip
Flops is the
present-state of the
variables
Dr. Clincy
Input, D, of the
Flip Flops is the
next-state of the
variables
Lecture
34
Finite State Machine Model
The example we just implemented is an example of a “Finite State Machine” - is a model
or abstraction of behavior composed of a finite number of states, transitions between
those states, and actions
Input
x
Output
z
y1
Combinational
logic
y2
Y1
Y2
Present
state
Next
state
Delay elements
(f lip-f lops)
Figure A.52. A formal model of a finite state machine.
Dr. Clincy
Lecture
35
Chapter 3 Review
If any time remains, we can review any topic or
concept for Chapter 3 that was covered in the
lectures. Please keep your questions geared
towards the concepts covered in Ch 3 and the
lectures (in realizing some value-added for the upand-coming exam)
Exam 2 will consists of two parts: Part 1 on Monday and Part 3
on Wednesday. Part 1 will be closed book (can use calculator,
can not use phone or laptop). Part 2 will be open book (can use
calculator and book, can’t use phone or laptop). If you miss
either part of the exam, it can not be made up.
Dr. Clincy
Lecture
Slide 36
CS3501 Exam 1 Results
• Average Score = 41 (Average Grade = 75)
• Score SD = 24 (very large)
Grading Scaled Used:
•
•
•
•
•
100-79 A-grade (3 students)
78-54 B-grade (6 students)
53-29 C-grade (7 students)
28-4 D-grade (10 students)
3-0
F-grade (0 students)
In getting your grade logged, be sure and pass back the exam
after we go over them
Dr. Clincy
37