Download Gravitation - WordPress.com

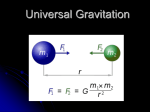
Gravitation
AP Physics C
Newton’s Law of Gravitation
What causes YOU to be pulled down? THE EARTH….or
more specifically…the EARTH’S MASS. Anything that
has MASS has a gravitational pull towards it.
Fg Mm
What the proportionality above is
saying is that for there to be a
FORCE DUE TO GRAVITY on
something there must be at least 2
masses involved, where one is
larger than the other.
N.L.o.G.
As you move AWAY from the earth, your
DISTANCE increases and your FORCE DUE
TO GRAVITY decrease. This is a special
INVERSE relationship called an InverseSquare.
1
Fg  2
r
The “r” stands for SEPARATION DISTANCE
and is the distance between the CENTERS OF
MASS of the 2 objects. We us the symbol “r”
as it symbolizes the radius. Gravitation is
closely related to circular motion as you will
discover later.
N.L.o.G – Putting it all together
m1m2
r2
G  constant of proportion ality
Fg 
G  Universal Gravitatio nal Constant
G  6.67 x10
Fg  G
 27
m1m2
r2
Fg  mg  Use this when you are on the earth
Fg  G
m1m2
 Use this when you are LEAVING th e earth
r2
Nm 2
kg 2
Try this!
Let’s set the 2 equations equal to each other since they BOTH
represent your weight or force due to gravity
Fg  mg  Use this when you are on the earth
Fg  G
m1m2
 Use this when you are LEAVING th e earth
2
r
Mm
r2
M
g G 2
r
M  Mass of the Earth  5.97 x10 24  kg
mg  G
r  radius of the Earth  6.37 x10 6  m
g=
GME
(RE + h )
2
SOLVE FOR g!
(6.67 x1027 )(5.97 x1024 )
2
g

9
.
81
m
/
s
(6.37 x106 ) 2
How did Newton figure this out?
Newton knew that the force on a falling apple (due to
Earth) is in direct proportion to the acceleration of that
apple. He also knew that the force on the moon is in
direct proportion to the acceleration of the moon,
ALSO due to Earth
Newton also surmised that that SAME force
was inversely proportional to the distance
from the center of Earth. The problem was
that he wasn’t exactly sure what the
exponent was.
How did Newton figure this out?
Since both the acceleration
and distance were set up as
proportionalities with the
force, he decided to set up
a ratio.
Newton knew that the
acceleration of the apple
was 9.8 and that the
approximate distance was
4000 miles to the center of
Earth.
Newton also knew the distance and acceleration of
the Moon as it orbits Earth centripetally. It was the
outcome of this ratio that led him to the exponent of
“2”. Therefore creating an inverse square relationship.
Newton’s Law of Gravitation (in more
detail)
To make the expression more mathematically
acceptable we also look at this formula this way:
The NEW "r" that you see is simply a unit vector
like I,j, & k-hat. A unit vector, remember, tells you
the direction the force is going. In this case it
means that it is between the two bodies is RADIAL
in nature. The NEGATIVE SIGN is meant to
denote that a force produces "bound" orbits. It is
only used when you are sure you need it relative
to whatever reference frame you are using
.....SO BE CAREFUL! It may be wise to use this
expression to find magnitudes only.
N.L.o.G.

In summary, Newton’s law of universal
gravitation states:

“Every particle in the Universe attracts every other
particle with a force that is directly proportional to
the product of their masses and inversely
proportional to the square of the distance between
them.”
Gravitational Force Due to a
Distribution of Mass
The
gravitational force exerted by a finite-size, spherically
symmetric mass distribution on a particle outside the
distribution is the same as if the entire mass of the
distribution were concentrated at the center.
For example, the force exerted by the Earth on a particle
of mass m near the surface of the Earth is
ME m
Fg = G 2
RE
Section 13.1
Quick Quiz

A planet has two moons of equal mass. Moon
1 is in a circular orbit of radius r. Moon 2 is in
a circular orbit of radius 2r. What is the
magnitude of the gravitational force exerted
by the planet on Moon 2?





(a) 4 times as large as that on Moon 1.
(b) 2 times as large as that on Moon 1.
(c) Equal to that on Moon 1.
(d) ½ as large as that on Moon 1.
(e) ¼ as large as that on Moon 1.
Example
What is the gravitational force between the earth and a 100
kg man standing on the earth's surface?
M  Mass of the Earth  5.97 x1024  kg
r  radius of the Earth  6.37 x106  m
24
mmanM Earth
11 (100)(5.97 x10 )
Fg  G
 6.67 x10

2
6 2
r
(6.37 x10 )
9.81 x 102 N
Because the force near the surface of Earth is constant, we can define
this force easier by realizing that this force of gravitation is in direct
proportional to the man’s mass. A constant of proportionality must drive
this relationship. F  m
g
man  Fg  mman g
We see that this constant
is in fact the gravitational
9.81x102  100 g
acceleration located near
g  9.8 m / s / s
the Earth’s surface.
Example

Three 0.300 kg billiard balls are placed on a
table at the corners of a right triangle. The
sides of the triangles are of lengths a =
0.400 m, b = 0.300 m, and c = 0.500 m.
calculate the gravitational force vector on
the cue ball (designated m1) resulting from
the other two balls as well as the magnitude
and direction of this force.
Example
How far from the earth's surface must an astronaut in space
be if she is to feel a gravitational acceleration that is half
what she would feel on the earth's surface?
GM Earth
M
g G
r
 rEarth
2
(r  rearth )
g
11
24
Mm
(6.67 x10 )(5.97 x10 )
mg  G 2
r
 6.37 x10 6  2.64x106 m
r
4 .9
M
g G 2
r
This value is four tenths the
24
M  Mass of the Earth  5.97 x10  kg
radius of Earth.
r  radius of the Earth  6.37 x10 6  m
Quick Quiz

Superman stands on top of a very tall
mountain and throws a baseball horizontally
with a speed such that the baseball goes into
a circular obit around the Earth. While the
baseball is in orbit, what is the magnitude of
the acceleration of the ball?




(a) It depends on how fast the baseball is thrown.
(b) It is zero because the ball does not fall to the
ground.
(c) It is slightly less than 9.80 m/s2.
(d) It is equal to 9.80 m/s2.
Example

Using the known radius of the Earth and that g = 9.80 m/s2 at the
Earth’s surface, find the average density of the Earth.
Digging a hole
When you jump down and are at a radius “r” from the center,
the portion of Earth that lies OUTSIDE a sphere a radius “r”
does NOT produce a NET gravitational force on you!
The portion that lies INSIDE the sphere does. This implies
that as you fall the “sphere” changes in volume, mass, and
density ( due to different types of rocks)
r
3
M
4

r
3
  , Vsphere  4 3 r  M inside  
V
3
Mm
G 4m
G 4m
Fg  G 2  Fg 
r k
r
3
3
Fg  kr
This tells us that your “weight” actually
DECREASES as you approach the
center of Earth from within the INSIDE
of the sphere and that it behaves like
Hook’s Law. YOU WILL OSCILLATE.
The Gravitational Field
A
gravitational field exists at every point in
space.
When a particle of mass m is placed at a point
where the gravitational field is g, the particle
experiences a force.
The field exerts a force on the particle

Fg = mg
The GF
The
gravitational field is defined as
gº
The
Fg
m
gravitational field is the gravitational force
experienced by a test particle placed at that point divided
by the mass of the test particle.
The presence of the test particle is not necessary for the
field to exist.
The source particle creates the field.
The field can be detected and its strength measured by
placing a test particle in the field and noting the force
exerted on it.
The GF
The
gravitational field vectors
point in the direction of the
acceleration a particle would
experience if placed in that field.
The magnitude is that of the
freefall acceleration at that location.
Part B of the figure shows the
gravitational field vectors in a small
region near the Earth’s surface.
 The vectors are uniform in
both magnitude and direction.
The GF
gravitational field describes the “effect”
that any object has on the empty space around
itself in terms of the force that would be present
if a second object were somewhere in that
space.
The
Fg
GM
g=
= - 2 rˆ
m
r
Example

The International Space Station operates at
an altitude of 350 km. Plans for the final
construction show that material of weight
4.22 x 106 N, measured at the Earth’s
surface. Will have been lifted off the surface
by various spacecraft during the construction
process. What is the weight of the space
station when in orbit?
Planetary Motion
Ptolemy…
Copernicus…
Kepler
1571 – 1630
German astronomer
Best known for developing
laws of planetary motion


Based on the observations
of Tycho Brahe
Kepler's Laws
There are three laws that Johannes Kepler formulated when he
was studying the heavens
THE LAW OF ORBITS - "All planets move in elliptical orbits, with
the Sun at one focus.”
THE LAW OF AREAS - "A line that connects a planet to the sun
sweeps out equal areas in the plane of the planet's orbit in equal
times, that is, the rate dA/dt at which it sweeps out area A is
constant.”
THE LAW OF PERIODS - "The square of the period of any planet is
proportional to the cube of the semi major axis of its orbit."
Notes About Ellipses
F1
and F2 are each a focus
of the ellipse.
 They are located a
distance c from the
center.
 The sum of r1 and r2
remains constant.
The longest distance
through the center is the
major axis.
 a is the semi-major
axis.
Section 13.3
Notes About Ellipses, cont
The
shortest distance
through the center is the
minor axis.
 b is the semi-minor
axis.
The eccentricity of the
ellipse is defined as e = c /a.
 For a circle, e = 0
 The range of values of
the eccentricity for
ellipses is 0 < e < 1.
 The higher the value of
e, the longer and
thinner the ellipse.
Section 13.3
Orbital Eccentricity Examples
Mercury’s
orbit has the highest eccentricity of any planet.
Comet Halley’s orbit has a much higher eccentricity.
 e = 0.97
Section 13.3
Kepler’s 1st law – The Law of Orbits
"All planets move in elliptical orbits, with the
Sun at one focus.”
Notes About Ellipses, Planet Orbits
The
Sun is at one focus.
 It is not at the center of the ellipse.
 Nothing is located at the other focus.
Aphelion is the point farthest away from the Sun.
 The distance for aphelion is a + c.
 For an orbit around the Earth, this point is called the
apogee.
Perihelion is the point nearest the Sun.
 The distance for perihelion is a – c.
 For an orbit around the Earth, this point is called the
perigee.
Section 13.3
Kepler’s First Law
A
circular orbit is a special case of the general
elliptical orbits.
Is a direct result of the inverse square nature
of the gravitational force.
Elliptical (and circular) orbits are allowed for
bound objects.


A bound object repeatedly orbits the center.
An unbound object would pass by and not return.

These objects could have paths that are parabolas (e =
1) and hyperbolas (e > 1).
Section 13.3
Kepler’s 2nd Law – The Law of Areas
"A line that connects a planet to the sun sweeps out
equal areas in the plane of the planet's orbit in
equal times, that is, the rate dA/dt at which it
sweeps out area A is constant.”
Kepler’s Second Law
Is
a consequence of conservation
of angular momentum for an
isolated system.
Consider the planet as the
system.
Model the Sun as massive
enough compared to the planet’s
mass that it is stationary.
The gravitational force exerted by
the Sun on the planet is a central
force.
The force produces no torque, so
angular momentum is a constant.

L = r x p = MPr x v = constant
Section 13.3
Kepler’s Second Law, cont.
Geometrically,
in a time dt, the radius
vector r sweeps out the area dA, which
is half the area of the parallelogram .
dA =
Its
1
|r x dr|
2
displacement is given by
dr = vdt
Mathematically,
we can say
dA
L
=
= constant
dt 2M p
The
radius vector from the Sun to any
planet sweeps out equal areas in equal
times.
The law applies to any central force,
whether inverse-square or not.
Section 13.3
Kepler’s 3rd Law – The Law of Periods
"The square of the period of any planet is proportional
to the cube of the semi major axis of its orbit."
Gravitational forces are centripetal, thus
we can set them equal to each other!
Since we are moving in a circle we can
substitute the appropriate velocity formula!
The expression in the RED circle derived by setting
the centripetal force equal to the gravitational force
is called ORBITAL SPEED.
Using algebra, you can see that everything
in the parenthesis is CONSTANT. Thus the
proportionality holds true!
Fg = M p a ®
GMSunMPlanet
v2
= MP
r2
r
2p r
v=
T
æ 4p 2 æ 3
3
T2 = æ
ær = K S r
æGMSun æ
Kepler’s Third Law, cont.
This
can be extended to an elliptical orbit.
Replace r with a.
 Remember a is the semi-major axis.
æ 4p 2 ö 3
3
T =ç
a
=
K
a
÷
S
GM
Sun ø
è
2
Ks
is independent of the mass of the planet, and so is valid
for any planet.
If an object is orbiting another object, the value of K will
depend on the object being orbited.
For example, for the Moon around the Earth, KSun is
replaced with Kearth.
Section 13.3
Example

Calculate the mass of the Sun, noting that the period of
the Earth’s orbit around the Sun is 3.156 x 107 s, and its
distance from the Sun is 1.496 x 1011 m.
Example
Consider a satellite of mass m moving in a circular orbit around the
Earth at a constant speed v and at an altitude h above the Earth’s
surface as illustrated to the right. Determine the speed of the satellite in
terms of G, h, RE, and ME.
If the satellite is said to be geosynchronous ( that is , appearing to
remain over a fixed position on the Earth), how fast is it moving through
space?
Kinetic Energy in Orbit
Using our ORBITAL SPEED
derived from K.T.L and the
formula for kinetic energy
we can define the kinetic
energy of an object in a bit
more detail when it is in
orbit around a body.
The question is WHY? Why do we need a new equation for kinetic
energy? Well, the answer is that greatly simplifies the math. If we use
regular kinetic energy along with potential, we will need both the orbital
velocity AND the orbital radius. In this case, we need only the orbital
radius.