Download What is a Surd - Mr

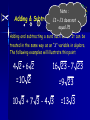
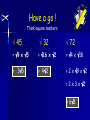
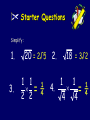
Surds
Simplifying a Surd
Rationalising a Surd
Conjugate Pairs
Starter Questions
Use a calculator to find the values of :
1.
3.
5.
3
36 = 6
2.
8
144 = 12
4.
4
16
2  1.41 6.
3
21  2.76
=3
=2
The Laws Of Surds
Learning Intention
1. To explain what a surd is
and to investigate the
rules for surds.
Success Criteria
1. Learn rules for surds.
1. Use rules to simplify surds.
What is a Surd
144 = 12
36 = 6
The above roots have exact values
and are called rational
2  1.41
3
21  2.76
These roots do NOT have exact values
and are called irrational OR
Surds
Note :
Adding & Subtracting
√2 +Surds
√3 does not
equal √5
Adding and subtracting a surd such as 2. It can be
treated in the same way as an “x” variable in algebra.
The following examples will illustrate this point.
4 2+6 2
16 23 - 7 23
=10 2
10 3 + 7 3 - 4 3
=9 23
=13 3
First Rule
a  b  ab
Examples
4  6  24
4  10  40
List the first 10 square numbers
1, 4, 9, 16, 25, 36, 49, 64, 81, 100
Simplifying Square Roots
Some square roots can be broken down into a
mixture of integer values and surds. The following
examples will illustrate this idea:
12
= 4 x 3
= 2 3
To simplify 12 we must split 12
into factors with at least one being
a square number.
Now simplify the square root.
Have a go !
Think square numbers
 45
 32
 72
= 9 x 5
= 16 x 2
= 4 x 18
= 35
= 42
= 2 x 9 x 2
= 2 x 3 x 2
= 62
What Goes In The Box ?
Simplify the following square roots:
(1)  20
(2)  27
(3)  48
= 25
= 33
= 43
(4)  75
(5)  4500
(6)  3200
= 53
= 305
= 402
Starter Questions
Simplify :
1.
3.
20 = 2√5 2.
1 1
 =
2 2
¼
18 = 3√2
1
1
4.

=
4
4
¼
The Laws Of Surds
Learning Intention
1. To explain how to
rationalise a fractional
surd.
Success Criteria
1. Know that √a x √a = a.
2. To be able to rationalise the
numerator or denominator of
a fractional surd.
Second Rule
a a  a
Examples
4 4  4
13  13  13
Rationalising Surds
You may recall from your fraction work that the
top line of a fraction is the numerator and the
bottom line the denominator.
2
numerator
=
3 denominator
Fractions can contain surds:
2
3
5
4 7
3 2
3- 5
Rationalising Surds
If by using certain maths techniques we remove the
surd from either the top or bottom of the fraction
then we say we are “rationalising the numerator” or
“rationalising the denominator”.
Remember the rule
a a  a
This will help us to rationalise a surd fraction
Rationalising Surds
To rationalise the denominator multiply the top and
bottom of the fraction by the square root you are
trying to remove:
3
3
5
=

5
5
5
3 5
=
5
( 5 x 5 =  25 = 5 )
Rationalising Surds
Let’s try this one :
Remember multiply top and bottom by root you are
trying to remove
3
3 7
3 7
3 7
=
=
=
14
2 7 2 7  7 2 7
Rationalising Surds
Rationalise the denominator
10
10  5
10 5 2 5
=
=
=
7 5 7 5  5 7 5
7
What Goes In The Box ?
Rationalise the denominator of the following :
7
3
4
9 2
7 3
=
3
2 2

9
4
6
2 6
=
3
14
3 10
=
2 5
7 3
2 15
=
21
6 3
11 2
3 6
=
11
7 10
15
Starter Questions
Conjugate Pairs.
Multiply out :
1.
3  3= 3
2.
14  14 = 14
3.

12 + 3


12 - 3 = 12- 9 = 3
The Laws Of Surds
Conjugate Pairs.
Learning Intention
1. To explain how to use the
conjugate pair to
rationalise a complex
fractional surd.
Success Criteria
1. Know that
(√a + √b)(√a - √b) = a - b
2. To be able to use the
conjugate pair to rationalise
complex fractional surd.
Looks
something like
the difference
of two squares
Rationalising Surds
Conjugate Pairs.
Look at the expression :
( 5  2)( 5  2)
This is a conjugate pair. The brackets are identical
apart from the sign in each bracket .
Multiplying out the brackets we get :
( 5  2)( 5  2) = 5 x5 - 2 5 + 2 5 - 4
=5-4 =1
When the brackets are multiplied out the surds
ALWAYS cancel out and we end up seeing that the
expression is rational ( no root sign )
Rationalising Surds
Conjugate Pairs.
Rationalise the denominator in the expressions below by
multiplying top and bottom by the appropriate
conjugate:
2
5-1
2( 5 + 1)
=
( 5 - 1)( 5 + 1)
2( 5 + 1)
2( 5 + 1)
=
=
( 5  5 - 5 + 5 - 1)
(5 - 1)
( 5 + 1)
=
2
Rationalising Surds
Conjugate Pairs.
Rationalise the denominator in the expressions below
by multiplying top and bottom by the appropriate
conjugate:
7
( 3 - 2)
7( 3 + 2)
=
( 3 - 2)( 3 + 2)
7( 3 + 2)
=
(3 - 2)
= 7( 3 + 2)
What Goes In The Box
Rationalise the denominator in the expressions below :
5
( 7-2)
5( 7 + 2)
=
3
3
=3+
( 3 - 2)
6
Rationalise the numerator in the expressions below :
6+4
12
-5
=
6( 6 - 4)
5 + 11
7
-6
=
7( 5 - 11)