Download 04-Probability Theory and Random Variables

History of Probability Theory
 Started in the year of 1654
De Mere (a well-known gambler) asked a question to Blaise
Pascal (a mathematician)
Whether to bet on the following event?
“To throw a pair of dice 24 times, if a ‘double six’ occurs at least once, then win.”
correspond
Blaise Pascal
4/30/2017
Pierre Fermat
BUS304 – Probability Theory
1
Applications of Probability Theory
 Gambling:
 Poker games, lotteries, etc.
 Weather report:
 Likelihood to rain today
 Power of Katrina
 Many more in modern business world
 Risk Management and Investment
• Value of stocks, options, corporate debt;
• Insurance, credit assessment, loan default
 Industrial application
• Estimation of the life of a bulb, the shipping date, the daily production
4/30/2017
BUS304 – Probability Theory
2
Concept: Experiment and event
 Experiment: A process that
produces a single outcome
whose result cannot be
predicted with certainty.
Example:
Experiment
Experimental Outcomes
Toss a coin
Head, tail
Inspect a part
Defective, nondefective
Play a football game
Win, lose, tie
Roll a die
 Event: A certain outcome obtained in an experiment.
Example of an event (description of outcome)
 Two heads in a row when you flip a coin three times;
 At least one “double six” when you throw a pair of dice 24 times.
4/30/2017
BUS304 – Probability Theory
3
Description of Events
 Elementary Events
 The most rudimentary outcomes resulting from a simple
experiment
 Throwing one die, “obtaining a
” is an elementary event
 Denoted as “e1, e2, …, en”
Note: the elementary events cannot be further divided
into smaller events.
e.g. flip a coin twice, how many elementary events
you expect to observe?
• “getting one head one tail” is NOT an elementary event.
• Elementary events are {HH, HT, TH, TT}
4/30/2017
BUS304 – Probability Theory
4
Description of Events
 Sample Space:
 Collection of all elementary outcomes:
 In many experiments, identifying sample space is important.
 Write down the sample space of the following experiments:
• throwing a pair of dice.
• flipping a coin three times.
• drawing two cards from a bridge deck.
 An event (denoted as E), can be represented as a
combination of elementary events.
 E.g. E = A die shows number higher than 3
Elementary events: e1 =
4/30/2017
; e2 =
; e3 =
BUS304 – Probability Theory
.
5
Rules of Assigning Probabilities
Three rules are commonly used:
 Classical Probability Assessment
 Relative Frequency Assessment
 Subjective Probability Assessment
4/30/2017
BUS304 – Probability Theory
6
Basic Rules to assign probability (1)
Classical probability Assessment:
P(E) =
Number of Elementary Events
Total number of Elementary Events
Exercise:
Decide the probability of the
following events
1. Get a card higher than 10 from a
where:
• E refers to a certain event.
• P(E) represents the probability of the event E
bridge deck
2. Get a sum higher than 11 from
throwing a pair of dice.
When to use this rule?
3. John and Mike both randomly pick
When the chance of each elementary event
is the same:
e.g. cards, coins, dices, use random number
generator to select a sample
4/30/2017
a number from 1-5, what is the
chance that these two numbers
are the same?
BUS304 – Probability Theory
7
Basic Rules to assign probability (2)
 Relative Frequency of Occurrence
Probability of Future Event = Relative Freq. of Past =
Number of times E occurs
N
Examples:
 If a survey result says, among 1000 people, 600 prefer iphone to ipod touch, then
you assign the probability that the next person you meet will like iphone is 60%.
 A basketball player’s percentage of made free throws. Why do you think Yao Ming
has a better chance to win the free throw competition than Shaq O’Neal?
 The probability that a TV is sent back for repair? Based on past experience.
 The most commonly used in the business world.
4/30/2017
BUS304 – Probability Theory
8
Exercise
A clerk recorded the number of patients waiting
for service at 9:00am on 20 successive days
Number of waiting
Number of Days Outcome Occurs
0
2
1
5
2
6
3
4
≥4
3
Total
20
Assign the probability that there are at most 2 agents waiting at 9:00am.
4/30/2017
BUS304 – Probability Theory
9
Exercise 4.1 (Page 137)
Male
Female
Under 20
168
208
20 to 40
340
290
Over 40
170
160
Elementary Events?
Sample Space?
a) Probability that “a customer is a male”?
b) Probability that “a customer is 20 to 40 years old”?
c) Probability that “a customer being 20 to 40 years old
and a male”?
4/30/2017
BUS304 – Probability Theory
10
Basic Rules to assign probability (3)
 Subjective Probability Assessment
 Subjective probability assessment has to be used when there is not
enough information for past experience.
 Example1: The probability a player will make the last minute shot (a
complicated decision process, contingent on the decision by the
component team’s coach, the player’s feeling, etc.)
 Example2: Deciding the probability that you can get the job after the
interview.
•
•
•
•
•
Smile of the interviewer
Whether you answer the question smoothly
Whether you show enough interest of the position
How many people you know are competing with you
Etc.
 Always try to use as much information as possible.
 As the world is changing dramatically, people are more and more rely upon subjective assessment.
4/30/2017
BUS304 – Probability Theory
11
Summary of Basic Approaches
 Classical Rule
 Elementary events have equal odds
 Relative Frequency
 Use relative frequency table. Probability assigned based on
percentage of occurrence.
 Subjective
 Based on experience, combining different signals to make
inference. No standard approach to have people agree on each
other.
No matter what method used, probability cannot be
higher than 1 or lower than 0!
4/30/2017
BUS304 – Probability Theory
12
Rules for complement events
 what is the a complement event?
E
E
 The Rule: P( E )  1  P(E)
If Obama’s chance of winning the presidential campaign is assigned to be 60%,
that means McCain’s chance is 1-60% = 40%.
If the probability that at most two patients are waiting in the line is 0.65, what is the
complement event? And what is the probability?
4/30/2017
BUS304 – Probability Theory
13
Composite Events
 E = E1 and E2
=(E1 is observed) AND (E2 is also observed)
E1
E2
P(E1 and E2) ≤ P(E1)
P(E1 and E2) ≤ P(E2)
P(E1 and E2)
 E = E1 or E2
= Either (E1 is observed) Or (E2 is observed)
E1
E1 or E2
E2
P(E1 or E2) ≥ P(E1)
P(E1 or E2) ≥ P(E2)
More specifically, P(E1 or E2) = P(E1) + P(E2) - P(E1 and E2)
4/30/2017
BUS304 – Probability Theory
14
Exercise
Male
Female
Total
Under 20
168
208
376
20 to 40
340
290
630
Over 40
170
160
330
Total
678
658
1336
1. What is the probability of selecting a person who is a male?
2. What is the probability of selecting a person who is under 20?
3. What is the probability of selecting a person who is a male and
also under 20?
4. What is the probability of selecting a person who is either a male
or under 20?
4/30/2017
BUS304 – Probability Theory
15
Mutually Exclusive Events
 If two events cannot happen simultaneously, then these
two events are called mutually exclusive events.
 Ways to determine whether two events are mutually
exclusive:
 If one happens, then the other cannot happen.
Examples:
 Draw a card, E1 = A Red card, E2 = A card of club
 Throwing a pair of dice, E1 = one die shows
E2 = a double six.
 All elementary events are
E2
E1
mutually exclusive.
 Complement Events
4/30/2017
BUS304 – Probability Theory
16
Rules for mutually exclusive events
If E1 and E2 are mutually exclusive, then
 P(E1 and E2) = ?
 P(E1 or E2) = ?
E1
E2
Exercise:
 Throwing a pair of dice, what is the probability that I
get a sum higher than 10?
 E1: getting 11
 E2: getting 12
 E1 and E2 are mutually exclusive.
 So P(E1 or E2) = P(E1) + P(E2)
4/30/2017
BUS304 – Probability Theory
17
Conditional Probabilities
 Information reveals gradually, your estimation changes
as you know more.
 Draw a card from bridge deck (52 cards). Probability of
a spade card?
 Now, I took a peek, the card is black, what is the probability of a
spade card?
 If I know the card is red, what is the probability of a spade card?
 What is the probability of E1?
 What if I know E2 happens, would you
E1
E2
change your estimation?
4/30/2017
BUS304 – Probability Theory
18
Bayes’ Theorem
 Conditional Probability Rule:
PE1 and E2 
PE1 | E2  
P  E2 
Example:
GPA3.0
GPA<3.0
Male
282
323
Female
305
318
P(“Male”)=?
P(“Male” and “GPA<3.0”)=?
P(“GPA<3.0” | “Male”) = ?
4/30/2017
Thomas Bayes
(1702-1761)
P(“GPA 3.0”)=?
P(“Female” and “GPA 3.0”)=?
P (“Female” | “GPA 3.0”)=?
BUS304 – Probability Theory
19
Independent Events
 If PE1 | E2   PE1 
then we say that “Events E1 and E2 are independent”.
That is, the outcome of E1 is not affected by whether E2
occurs.
 Typical Example of independent Events:
 Throwing a pair of dice, “the number showed on one die” and
“the number on the other die”.
 Toss a coin many times, the outcome of each time is
independent to the other times.
Independen t : PE1 and E2   PE1  PE2 
How to prove?
20
Exercise
1. Calculate the following probabilities:
a) Prob of getting 3 heads in a row?
b) Prob of a “double-six”?
c) Prob of getting a spade card which is also higher than 10?
2. Data shown from the following table. Decide whether the following
events are independent?
a) “Selecting a male” versus “selecting a female”?
b) “Selecting a male” versus “selecting a person under 20”?
Male
Female
Under 20
168
208
20 to 40
340
290
Over 40
170
160
4/30/2017
BUS304 – Probability Theory
21
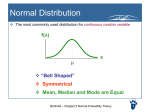
Probability Distribution
 Random Variable:
 A variable with random (unknown) value.
Examples
1. Roll a die twice: Let x be the number of times 4 comes up.
x = 0, 1, or 2
2. Toss a coin 5 times: Let x be the number of heads
x = 0, 1, 2, 3, 4, or 5
3. Same as experiment 2: Let’s say you pay your friend $1
every time head shows up, and he pays you $1 otherwise. Let x
be amount of money you gain from the game.
What are the possible values of x?
4/30/2017
BUS304 – Probability Theory
22
Discrete vs. Continuous
Random variables
Random Variables
Discrete
Examples:
4/30/2017
Continuous
Examples:
Number of students
showed up next time
The temperature
tomorrow
Number of late apt.
rental payments in Oct.
The total rental payment
collected by Sep 30
Your score in this
coming mid-term exam
The expected lifetime
of a new light bulb
BUS304 – Probability Theory
23
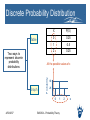
Discrete Probability Distribution
Table
Two ways to
represent discrete
probability
distributions
X
P(X)
0
0.25
1
0.5
2
0.25
Graph
Probability
All the possible values of x
.50
.25
0
4/30/2017
1
BUS304 – Probability Theory
2
x
24
Exercise
 Describe the probability distribution of the
random variables:

Draw a pair of dice, x is the random variable
representing the sum of the total points.
Step 1: Write down all the possible values in left column

Step 1.1: Write down the sample space
Step 2: Write down the corresponding probabilities
4/30/2017
BUS304 – Probability Theory
25
Measures of Discrete
Random Variables
Expected value of a discrete distribution
 An weighted average, taking into account the probability
 The expected value of random variable x is denoted as E(x)
E(x)= xi P(xi)
E(x)= x1P(x1) +x2P(x2) + … + xnP(xn)
Example:
What is your expected gain when you play the flip-coin game twice?
x
-2
0
2
4/30/2017
P(x)
.25
.50
.25
E(x) = (-2) * 0.25 + 0 * 0.5 + 2 * 0.25
=0
Your expected gain is 0! – a fair game.
BUS304 – Probability Theory
26
Spreadsheet to compute
the expected value
 Step1: develop the distribution table according to the description of
the problem.
 Step2: add one (3rd) column to compute the product of the value
and the probability
 Step3: compute the sum of the 3rd column  The Expected Value
4/30/2017
x
P(x)
x*P(x)
-2
0.25
-2*.25=-0.5
0
0.5
0*0.5=0
2
0.25
2*0.25=0.5
E(x) =-0.5+0+0.5=0
BUS304 – Probability Theory
27
Exercise
You are working part time in a restaurant. The amount of tip you
get each time varies. Your estimation of the probability is as follows:
$ per night
Probability
50
0.2
60
0.3
70
0.4
80
0.1
You bargain with the boss saying you want a more fixed income.
He said he can give you $62 per night, instead of letting you keep
the tips. Would you want to accept this offer?
4/30/2017
BUS304 – Probability Theory
28
More Exercise
Buy lottery: price $10
 With 0.0000001 chance, you can win $1million
 With 0.001 chance, you can win $1000
 With 0.1 chance, you can win $50
What is the expected gain of buying this lottery ticket?
Is buying lottery a fair game?
Rule for expected value
If there are two random variables, x and y. Then
E(x+y) = E(x) + E(y)
 Example: “Head -$2”, “Tail +1”
• x is your gain from playing the game the first time
• y is your gain from playing the game the second time
• x+y is your total gain from playing the two games.
x
P(x)
y
P(y)
-2
0.5
-2
0.5
1
0.5
1
0.5
E(x)= -0.5
4/30/2017
E(y)= -0.5
Write down the probability
distribution of x+y and calculate
the expected value for x+y
Is this game a fair game?
BUS304 – Probability Theory
30
Exercise
Assume that the expected payoff of playing the
slot machine is -0.04 cents
What is the expected payoff when playing 100
times? 10,000 times?
Measure of risk-- variance
Two games
 Flip a coin once, if head then you get $1, otherwise
you pay $1;
 Flip a coin once, if head then you get $100,
otherwise you pay $100;
 Which game will you choose?
Three basic types of people
 Risk-lover
 Risk-neutral
 Risk-averse
What is your type?
Measures – variance
 Variance: a weighted average of the squared deviation from the
expected value.
x
P(x)
x – E(x)
(x-E(x))2
(x-E(x))2P(x)
50
0.2
50-64=-$14
(-14)2=196
196*0.2=39.6
60
0.3
-$4
16
4.8
70
0.4
$6
36
14.4
80
0.1
$16
256
25.6
84.4 (sum of above)
Step 1: develop the probability distribution table.
Step 2: compute the mean E(x): 50x0.2+60x0.3+70x0.4+80x0.1=64
Step 3: compute the distance from the mean for each value (x-E(x))
Step 4: square each distance (x – E(x))2
Step 5: weight the squared distance: (x-E(x))2P(x)
Step 6: sum up all the weighted square distance  variance
4/30/2017
BUS304 – Probability Theory
33
Variance and Standard deviation
 Variance
 The variance of a random
variable has the same
meaning as the variance of
population
 Calculation is the same as
calculating population
 Standard deviation of a
random variable:
 Same of the population
standard deviation
 Calculate the variance
 Then take the square root
of the variance.
 Written as sd(x) or

variance using a relative
e.g. for the example on page 10
frequency table.
 Written as var(x) or  2
4/30/2017
  84.4  9.19
BUS304 – Probability Theory
34
More exercise:
Page 4.66
4/30/2017
BUS304 – Probability Theory
35