* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Circles - Northwest ISD Moodle
Line (geometry) wikipedia , lookup
Rational trigonometry wikipedia , lookup
Problem of Apollonius wikipedia , lookup
Euclidean geometry wikipedia , lookup
Trigonometric functions wikipedia , lookup
Perceived visual angle wikipedia , lookup
Tangent lines to circles wikipedia , lookup
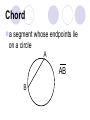
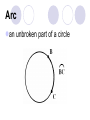
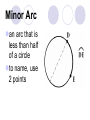
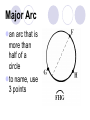
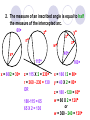
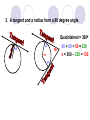
Circles Definitions Chord a segment whose endpoints lie on a circle A AB B Arc an unbroken part of a circle Minor Arc an arc that is less than half of a circle to name, use 2 points Major Arc an arc that is more than half of a circle to name, use 3 points Central Angle an angle whose vertex is at the center of a circle Inscribed Angle an angle whose vertex is on a circle and whose sides are chords of the circle Tangent a line, ray, or segment that is in the same plane as the circle, but intersects the circle in only one point Secant a line, ray, or segment that contains a chord Warm Up #1 Write an example of each of the following: A. Radius ____ B. Secant ____ C. Tangent ____ D. Chord ____ E. Diameter ____ F. Minor arc ____ G.Major arc ____ H. Central angle ____ I. Inscribed angle ____ J. Center ____ Circles Central and Inscribed Angles 1. The measure of an arc is the same as the measure of its central angle. y x If x = 63, Then y = 63 y 80 x 70 x = 70 y = 360 – (80 + 70) = 210 2. The measure of an inscribed angle is equal to half the measure of the intercepted arc. 60 z y x n z w 40 x 115 x = 60/2 = 30 z = 115 X 2 = 230 r = 360 - 230 = 130 OR 180-115 = 65 65 X 2 = 130 160 x = 160 / 2 = 80 y = 40 X 2 = 80 z = 180 - 120 = 60 w = 60 X 2 = 120 or w = 360 - 240 = 120 3. A tangent and a radius form a 90 degree angle. Quadrilateral = 360 50 x 90 + 90 + 50 = 230 x = 360 – 230 = 130 4. The measure of an angle formed by secants tangents or one of each is equal to half the difference of the intercepted arcs. xº 85 xº 250 15 125 110 150 X = (125-85) /2 = 20 120 xº X = (120-15) /2 = 52.5 X = (250-110)/2 = 70 5. The measure of the angle formed by two chords is equal to half the sum of the intercepted arcs. xº 50 80 102 88 y 78 xº 56 X = (50+80)/2 = 65 xº Y = (102 + 88) /2 = 95 180-95 = x = 85 (78+x)/2 = 56 (78+x) = 112 X = 34 Congruent chords = Congruent arcs 60 x y 45 x 12