Download MOSFET Small Signal Model and Analysis •Just as we did

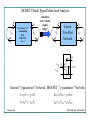
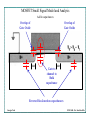
MOSFET Small Signal Model and Analysis
•Just as we did with the BJT, we can consider the
MOSFET amplifier analysis in two parts:
•Find the DC operating point
•Then determine the amplifier output parameters for very
small input signals.
Georgia Tech
ECE 3040 - Dr. Alan Doolittle
MOSFET Small Signal Model and Analysis
i1
+
V1
-
Non-Linear I-V
relationship
(BJT,
MOSFET,
etc…)
i2
+
V2
-
Linearize
over “small
signal
range”
i1
+
V1
-
Linear
Two Port
Network
i2
+
V2
-
iDS
iGS
vDS
vGS
General “y-parameter” Network MOSFET “y-parameter” Network
Georgia Tech
I1=y11V1 + y12V2
IGS=y11VGS + y12VDS
I2=y21V1 + y22V2
IDS=y21VGS + y22VDS
ECE 3040 - Dr. Alan Doolittle
MOSFET Small Signal Model and Analysis
[ =[ [
[[
[
IGS
y11
y12
VGS
IDS
y21
y22
VDS
y ij =
∂I j
∂Vi
VGS ,Q , VDS ,Q
IGS=y11VGS + y12VDS
Derivative of current-voltage equation
evaluated at the Quiescent Point
IDS=y21VGS + y22VDS
MOSFET Amplifiers are biased into Saturation (or Active Mode)
I DS =
[
]
Kn
(VGS − VTN )2 (1 + λ V DS )
2
1.) Input Conductance
I GS = 0 ⇒
∂I GS
= 0 and
∂VGS
2.) Output Conductance
3.) Transconductance
Georgia Tech
for V DS ≥ VGS − VTN
∂I GS
=0 ⇒
∂V DS
y11 = 0 and y12 = 0
∂I DS
λ Kn
= y 22 =
(VGS − VT )2
∂VDS
2
∂I DS
= y 21 = K n (VGS − VT )(1 + λ VDS )
∂VGS
ECE 3040 - Dr. Alan Doolittle
MOSFET Small Signal Model and Analysis
Compare with BJT Results
There is a large amount of symmetry between the MOSFET and the BJT
MOSFET
y 22
BJT
λ Kn
I DS
2
(
)
= go =
VGS − VT =
1
2
+ V DS
λ
y 21 = g m = K n (VGS − VT )(1 + λ VDS ) =
Georgia Tech
Each of these
parameters
act in the
same manner
I DS
 VGS − VTN 


2


y 22
IC
=
V A + VCE
y 21 =
IC
VT
ECE 3040 - Dr. Alan Doolittle
MOSFET Small Signal Model and Analysis
Putting the mathematical model into a small signal equivalent circuit
Compare this to the BJT small signal equivalent circuit
Georgia Tech
ECE 3040 - Dr. Alan Doolittle
MOSFET Small Signal Model and Analysis
Example: Jaeger 13.94
Calculate the voltage gain, Av=vo/vs
Given: Kn=1 mA/V2 , λ=0.015 V-1
Bias Point of: IDS=2 mA, VDS=7.5V
Georgia Tech
ECE 3040 - Dr. Alan Doolittle
MOSFET Small Signal Model and Analysis
Example: Jaeger 13.94
go =
λ Kn
(VGS − VT )2
2
g m = K n (VGS − VT )(1 + λ VDS )
Need to find VGS-VT
[
]
Kn
I DS =
(VGS − VTN )2 (1 + λ VDS )
2
1 mA / V 2
2 mA =
(VGS − VTN )2 (1 + 0.015 (7.5) )
2
4
VGS − VTN =
= 1.9V
1.11
∴ g m = 2.11 mS g o = 27.1 µ S ⇒ ro = 36.9kΩ ECE 3040 - Dr. Alan Doolittle
[
Georgia Tech
]
MOSFET Small Signal Model and Analysis
Example: Jaeger 13.94
Av =
vo vGS vo
=
vs
v s vGS
vGS
1Meg
=
= 0.99 and
10k + 1Meg
vs
∴ Av =
Georgia Tech
vo
= − g m (ro
vGS
Rd
R3) = −2.1mS (3.48k ) = −7.35
vo vGS vo
=
= −7.27 [V / V ]
vs
v s vGS
ECE 3040 - Dr. Alan Doolittle
MOSFET Small Signal Model and Analysis
Add in capacitances
Overlap of
Gate Oxide
Overlap of
Gate Oxide
LD
LD
Gate to
channel to
Bulk
capacitance
Reverse Bias Junction capacitances
Georgia Tech
ECE 3040 - Dr. Alan Doolittle
MOSFET Small Signal Model and Analysis
Complete Model of a MOSFET
Overlap of
Gate Oxide
Overlap of
Gate Oxide
and Gate to
channel
capacitance
Georgia Tech
Gate to
channel to
Bulk
capacitance
g mb = g m
γ
2 V SB + 2φ F
Due to effective
modulation of the
threshold voltage.
Reverse Bias Junction capacitances
ECE 3040 - Dr. Alan Doolittle
MOSFET Small Signal Model and Analysis
SPICE MOSFET Model
SPICE models the drain current ( IDS ) of an n-channel MOSFET using the
following parameters/equations (SPICE variables are shown in ALL
CAPPITAL LETTERS)
Cutoff:
IDS = 0
Linear:
I DS =
KP  W

2  LEFF

V DS [2(VGS − VTH ) − V DS ](1 + (LAMBDA) V DS )

KP  W

2  LEFF

 (VGS − VTH )2 (1 + (LAMBDA) VDS )

Saturation:
I DS =
[
Threshold Voltage:
]
(
VTH = VTO + GAMMA 2 PHI − VBS − 2 PHI
)
Channel Length
LEFF=L-2LD
Georgia Tech
ECE 3040 - Dr. Alan Doolittle
MOSFET Small Signal Model and Analysis
SPICE MOSFET Model – Additional Parameters
SPICE takes many of it’s parameters from the integrated circuit
layout design:
W
AS=WxLdiff(source)
PS=2xLdiff(source)+W
AD=WxLdiff(drain)
L
Ldiff(source)
Source
PD=2xLdiff(drain)+W
Ldiff(drain)
Gate
L = polysilicon gate length
W = polysilicon gate width
AD = drain area
AS = source area
Drain
PD = perimeter of drain diffusion (not including edge under gate)
PS = perimeter of source diffusion (not including edge under gate)
NRD = number of “squares” in drain diffusion
NRS = number of “squares” in source diffusion
Georgia Tech
Specified in terms of the
minimum feature size
ECE 3040 - Dr. Alan Doolittle
MOSFET Small Signal Model and Analysis
SPICE MOSFET Model – Additional Parameters
Most
Used
Georgia Tech
ECE 3040 - Dr. Alan Doolittle
MOSFET Amplifiers
What is the Maximum Gain Possible?
Is it saturated (Constant current)?, VDS > VGS − VTP
but VDS = VGS
and VTP ≥ 0 for a depletion mode MOSFET so,
0 > −VTP is always satisfied. ⇒ Is Saturated!
AC
Signal
Gate
Bias
Av , Max = − g m vo
Av , Max = −
Av , Max = −
Georgia Tech
K n (VGS − VT )(1 + λ VDS )
λ K n (VGS − VT )
(1 + λ VDS )
λ (VGS − VT )
2
go is internal to the
transistor and can not be
avoided. Any additional
resistor due to external
circuitry will lower the
gain. For this reason
current sources are often
used as the “load” instead
of bias resistors in
amplifier circuits.
ECE 3040 - Dr. Alan Doolittle