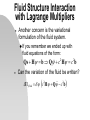Download Lagrange Multiplier Frames - University of Colorado Boulder

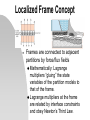
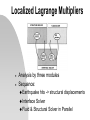
Coupling Heterogeneous Models
with Non-matching Meshes by
Localized Lagrange Multipliers
Modeling for Matching Meshes
with Existing Staggered
Methods and Silent Boundaries
Holly Lewis & Mike Ross
Center for Aerospace Structures
University of Colorado, Boulder
20 April 2004
Topics of Discussion





Refresh Memory
PML
Lagrange Multipliers for DamSandstone Interface
Future Work
Lagrange Multipliers for FluidStructure Interface and associate
issues
A Picture is Worth 1,000 Words
Multi-physic system
Modular Systems
Connected by Localized
Interaction Technique
(Black Lines)
Plan of Attack

Generate a benchmark model
 Use
current available methods
 Matching meshes

Generate a model with localized
frames
 Maintain

matching meshes
Generate a model with localized
frames
 With
nonmatching meshes
Benchmark Model
Refresher
Fluid (Spectral
Elements)
Dam (Brick
Elements)
Silent
Boundary
Soil (Brick
Elements)
Silent Boundary
•Output: Displacements of Dam & Cavitation Region
•Assume: Plane Strain (constraints reduce DOF)
•Only looking at seismic excitation in the x-direction
•Linear elastic brick elements
A Quick Note on Perfectly
Matched Layers
The main concept is to surround the computational domain at the
infinite media boundary with a highly absorbing boundary layer.


Outgoing waves are attenuated.
Wave amplitude


This boundary layer can be made of the same finite elements.
Formulation of the matrices are the same method for both computational
domain and the boundary layer

There are just different properties
A Quick Note on Perfectly
Matched Layers (PML)


Going from the frequency domain
to the time domain is a real pain!!!
Can be done see “Perfectly
Matched Layers for Transient
Elastodynamics of Unbounded
Domains.” U. Basu and A. Chopra
Localized Frame Concept

Frames are connected to adjacent
partitions by force/flux fields
 Mathematically:
Lagrange
multipliers “gluing” the state
variables of the partition models to
that of the frame.
 Lagrange multipliers at the frame
are related by interface constraints
and obey Newton’s Third Law.
Localized Lagrange Multipliers


Analysis by three modules
Sequance:
 Earthquake
hits -> structural displacements
 Interface Solver
 Fluid & Structural Solver in Parallel
Localized Lagrange Multipliers Applied to
Dam and Sandstone Interface
Dam
uD
uB
D
uS
s
Sandstone
Variational Principles and
Lagrange Multipliers

Lagrange Method to derive the equilibrium equations of a
system of constrained rigid bodies in Newtonian Mechanics
Formulation.
1- Treat the problem as if all bodies are entirely free and
formulate the virtual work by summing up the contributions of
each free body.
2- Identify constraint equations and multiply each by an
indeterminate coefficient. Then take the variation and add to
the virtual work of the free bodies to yield the total virtual work
of the system.
3- The sum of all terms which are multiplied by the same
variation are equated to zero. These equations will provide all
the conditions necessary for equilibrium.
Localized Lagrange Multipliers Applied to
Dam and Sandstone Interface
1- Subsystem Energy Expressions (Variational Formulation)
 D  f D )
System Dam : D  u D (K Du D  C Du D  M Du
 s  f s )
System Sandstone : S  u s (K s u s  C s u s  M s u
2- Identify Interface Constraints
 B  D (B1u D  u B )  S (B 2u s  u B )
 B  D (B1u D  u B )  D (B1u D  u B )  S (B 2u s  u B )  S (B 2u s  u B )
3- Total Virtual Work = 0 ( Stationary)
δΠ  δΠB  δΠS  δΠD  0
 D  f D  B1D )  u S (K s u s  Cs u s  M s u
 s  f s  B 2s ) 
  u D (K Du D  CDu D  M Du
 D (B1T u D  u B )  S (BT2 u S  u B )  u B (S  D )
Localized Lagrange Multipliers Applied to
Dam and Sandstone Interface

d
d2
K

C

MD
D
 D
2
dt
dt


0



B1T



0


0

1


0


0
B1  



0



0
0

1


0 
0
0
0
B1
0
d
d2
K S  CS  2 M S
dt
dt
0
B2
0
0
0
BT2
0
0
0
 I1
 I2
0


0



 I 2424 





0
0 24024 


1


 26424

0  u D  f D 
   
   

0  u S  f S 
   
   
 I1    D    0 
   
   
 I 2   s   0 
   
   
0  u B   0 
0


0


0




B 2  0


1


0

0



0
0
0

0

0
0
1
0
0
1

Eq. (21)
Eq. (22)
Eq. (23)
Eq. (24)
Eq. (25)
0


0




 0
0148524 

 I


  33 
0 0



 


 0


 0 


0


158424

Localized Lagrange Multipliers Applied to
Dam and Sandstone Interface
Midpoint Integration Rule:
u
n 1 / 2
1
(t ) 2 n 1/ 2
n

 u  (t )u 
u
2
4
n
1
 n 1/ 2
u n 1/ 2  u n  (t )u
2
u n 1  2u n 1/ 2  u n
Rearrange in terms of velocity and
acceleration at half time step
u n 1/ 2 
2 n 1/ 2 2 n
u
 u
t
t
 n 1/ 2 
u
4
4
2 n
n 1/ 2
n
u

u  u
2
2
(t )
(t )
t
Localized Lagrange Multipliers Applied to
Dam and Sandstone Interface
Examine Eqn (21) with midpoint rule:
 nD1/ 2  B1nD1/ 2  f Dn 1/ 2
K D u nD1/ 2  C D u nD1/ 2  M D u
Insert Midpoint Rule for velocity and acceleration
 u nD1/ 2  [K D 

2
4
1 n 1 / 2
n 1 / 2
CD 
M
]
f

B

1 D
t
t 2 D D
 4
2 n 
 2 n
n
 C D  u   M D 
u  u 
2
t 
 t 
 t 
Apply Same Concept to Eqn (22) to get a
displacement of the sandstone at the half time step
Localized Lagrange Multipliers Applied to
Dam and Sandstone Interface
Look at Eqn (23) with the above eqns for the displacements:
B1T u nD1/ 2  u nB1/ 2
1


2
4
n 1 / 2
 B K D  C D 
M
 u nB1/ 2
D  B1 D
2
t
t 


T
1
1

  n 1/ 2
2
4
 2

 B K D  C D 
M
 C D  u nB  
D  f D
2
t
t 
 t 

 
T
1
 4
2 n 
n
M D 
u

u D 
D
2
t
 t 

Apply the same concept to Eqn (24). Then use Eqn (25) and
the two above equations to input into Matrix form
Localized Lagrange Multipliers Applied to
Dam and Sandstone Interface
1
 

2
4
B1T  K D  C D 
M D  B1
0
2
t
t 
 

1



2
4
T

0
B 2  K S  C S 
M S  B 2
2


t



t




I 2424
I 2424



I 2424   n 1 2  g 
D
 D 



  
I 2424   nS1 2    g S 

  

  
0  u nB1 2   0 




2
4
g D  B1T K D  CD 
M
t
t 2 D 

1
 n1 2
 4
2 n 
 2 n
n

f

C
u

M
u

u D 
D
D
D
D
D
2

t

t



 t 



2
4
g S  BT2 K S  CS 
M
t
t 2 S 

1
 n1 2
 4
2 n 
 2 n
n

f

C
u

M
u

u S 


S
S
S
S
S
2

t

t



t





Localized Lagrange Multipliers Applied to
Dam and Sandstone Interface
Basic Concept:
Step 1: Solve for ’s using previous three equations.
Step 2: In parallel solve for the displacements at the
next time step using:
u nD1/ 2  [K D 

2
4
1 n 1 / 2
n 1 / 2
CD 
M
]
f

B

1 D
t
t 2 D D
 4
2 n 
 2 n
n
 C D  u D   M D 
u D  u D 
2
t
 t

 t 

Step 3: Update the variables and generate the
necessary time step-dependent vectors.
u nD1  2u nD1/ 2  u nD
Localized Lagrange Multipliers Applied to
Dam and Sandstone Interface
Dam Crest Displacement
with Lagrange Multipliers
Dam Crest Displacement
with Monolithic Model
Set Sail for the Future






Find bug in the Dam-Sandstone Interface
Develop structure-fluid interaction via localized
interfaces with nonmatching meshes.
Develop structure-soil interaction via localized
interfaces spanning a range of soil media.
Develop a localized interface for cavitating fluid
and linear fluid.
Develop rules for multiplier and connector frame
discretization.
Implement and assess the effect of dynamic
model reduction techniques.
Fluid Structure Interaction with
Lagrange Multipliers



Same Concept as with DamSandstone Interface
Separate the two systems
Apply interface Constraint
 B  D (u D  u B )   f (u f  u B )

However, remember the displacement
of the fluid is expressed in terms of the
gradient of a scalar function
u f    
Fluid Structure Interaction with
Lagrange Multipliers

Can the interface constraint be written?
 B  D (u D  u B )   f (   u B )
 B  B (u D  u B )  D (u D  u B )   f (   u B )   f (   u B )

What happens with the gradient?
Fluid Structure Interaction
with Lagrange Multipliers

Another concern is the variational
formulation of the fluid system.
 If
you remember we ended up with
fluid equations of the form:
Qs  H  b  Q  c 2 H  c 2b

Can the variation of the fluid be written?
 fluid   c 2 H  Q  c 2b
Fluid Structure Interaction
with Lagrange Multipliers
????????????????

d
d2
K D  C D  2 M D
dt
dt


0



B1T



0


0

0
B1
0
d2
c H 2 Q
dt
0
B 2
0
0
0
BT2
0
0
0
 I1
 I2
2

0  u D   f D 
   
   
    c 2 b 
0 
   
   
 I1    D    0 
   
   
 I2  fs   0 
   
   
0  u B   0 
Acknowledgments




NSF Grant CMS 0219422
Professor Felippa & Professor Park
Mike Sprague (Professor Geer’s Ph.D
student, now a post-doc in APPM)
CAS (Center for Aerospace Structures) CU