* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Sexuality-Based Model for HIV/AIDS with the Effect of Immigration
Survey
Document related concepts
Transcript
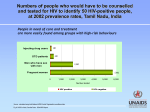
Sexuality-Based Model for HIV/AIDS with the Effect of Immigration and Emigration Pratibha Rani1, V.P. Saxena2, D.S. Hooda1 1 Department of Mathematics, Jaypee University of Engineering & Technology, Guna (M.P.) Email: [email protected]. Email: [email protected] 2 Department of Mathematics, Sagar Institute of Research & Technology, Bhopal (M.P.) Email: [email protected] Abstract In this paper, a nonlinear mathematical model for heterosexual transmission of HIV/AIDS epidemic with the effect of immigration and emigration is proposed. Here, the total adult population is divided into three different classes: male, female and female sex workers. The results of the model are analyzed by using stability theory of differential equations and also, the numerical simulation is implemented. This paper has been influenced by the importance of female sex workers in the -transmission of the HIV/AIDS. Keywords: HIV/AIDS, Immigration, Emigration, Female Sex Workers, Stability. 1. Introduction One of the most important public-health problem in developing countries is the Acquired Immune Deficiency Syndrome (AIDS) epidemic, which is caused by Human Immunodeficiency Virus (HIV). The first case of AIDS was recognized in 1981 and every year the number of infected people rises rapidly. As per the estimates of WHO and UNAIDS in 2013, approximately 35 million people were living with HIV globally. Of these, around 17.2 million were men, 16 million were women and 3.2 million were less than 15 years old. In the same year, around 2.1 million people were becoming newly infected and 1.5 million died of AIDS. HIV prevalence in India varies geographically [9, 10, 11, 20]. The four states in India with the highest numbers of people living with HIV are Andhra Pradesh, Karnataka, Maharashtra and Tamilnadu. HIV is primarily transmitted through unprotected sexual intercourse or blood transfusion. It is limited to those people who are capable to transmit HIV either by profession, such as sex workers, age group, social class, heredity such as mother to child transmissions, lifestyles which include drug users and misfortune those who acquired it by blood transfer [17]. As the infection progresses, the virus begins to reproduce itself and affects specific cells of the immune system, called CD4 cells. Within a few weeks, people are experiencing flu-like symptoms such as fever, headache, upset stomach and muscle aches. This stage of infection is called acute infection or primary HIV infection. It may last over 8-10 years depending on many factors and then the immune system has become seriously damaged. Over the time, HIV can destroy many of these CD4 cells and then the body can’t fight against disease. Thus, HIV infection contributes to AIDS. The life expectancy of an AIDS patient is 1 to 3 years [12]. In recent years, a sexually transmitted HIV infection poses an alarming threat in many countries. It ceased to increased death rates in various risk groups throughout the world. Currently, there are no known vaccines to protect HIV infection, but it is possible to protect yourself and others from infection through public awareness efforts. Therefore, it is relevant and important to investigate models for HIV/AIDS disease with different demographic structures in order to judge the influences of the disease along the population dynamics [2, 3, 7, 8]. Recently, because of high infection rates and large numbers of sexual partners, a sex worker has been considered as a core group for the transmission of HIV. Sex workers can increase the peril of infection of HIV and other sexually transmitted infections (STIs) by engaging in dangerous sexual behaviors. Female sex workers (FSW) form heterogeneous groups who have exchanged sex for money, goods and services. These groups are a critical effort for public health [9]. In some of the recent studies, it has been noted that HIV prevalence among female sex workers varies widely and it is more than 20 times higher than the HIV prevalence in the general population [4, 15]. Not only those sex workers, who are engrossed in sexual services, are at higher risk of HIV infection, but also who are unaware about their HIV status, can put in danger their own wellness and increases their danger of transmitting HIV infection. A mathematical model for HIV/AIDS disease is needed in order to obtain a numerical description of these trends and to make forecasts. In recent years, many studies have been made to model the transmission of infectious diseases and different issues like immigration, emigration, antiretroviral drugs, the role of sex workers etc., have been identified [2, 3]. May and Anderson [1] studied an HIV transmission dynamics model that represents the progression from HIV status of AIDS, where the population is split into categories of progressive infectious stages. They have been added various refinements into modeling frameworks [17]. A simple deterministic model has been proposed by Naresh and Omar [16], to study the transmission dynamics of HIV/AIDS in a population with variable size structure. Daabu and Seidu [6] developed a model to study the impact of migration on the spread of HIV/AIDS in South Africa using observed data. Bhunu et. al [5] presented a mathematical model to assess the link between prostitution and HIV transmission. Final results from this study suggest that effectively controlling HIV/AIDS calls for strategies that come up to both prostitution and HIV/AIDS transmission. In India, Eighty-five per cent of HIV transmission occurs through heterosexual contact with sex workers and their clients [20, 21]. A theoretical framework for the transmission of HIV/AIDS epidemic in India has been presented by Srinivasa Rao [18]. Kaur et. al [13] introduced a nonlinear mathematical model for studying the transmission dynamics of HIV/AIDS epidemic with emphasis on the role of female sex workers. The surroundings and context in which sex workers live and exercise do not affirm them to inhibit the risk factors [10, 11]. Because of these causes, sex workers have been seen a key population and in our opinion the interventions need to be planned and carried out to lead and empower this specific population if the epidemic is to be controlled [13, 14]. Thus, in the present analysis, the attempts are made to explore the role of female sex-workers, their clients in the transmission of HIV infection and also study the effect of immigration and emigration of the individuals in the population. In this paper, a nonlinear mathematical model is proposed for studying the transmission dynamics of HIV/AIDS in section 2. In section 3, analysis of the proposed model is discussed. The stability of the model is explained in section 4 and the numerical result for fixed values of parameters is discussed in section 5. 2. Mathematical Model The differential equations for the transmission dynamics of HIV/AIDS are given as follows: dSm 1 Sm 1 Sm I f 2 Sm I fs Sm 1 , dt dI m 1 Sm I f 2 Sm I fs (b1 ) I m I m , dt dAm b1 I m ( d ) Am , dt dS f dt 2 S f 3 S f I m S f 2 , dI f dt 3 S f I m (b2 ) I f I f , dAf dt dS fs dt b2 I f ( d ) Af , 3 4 S fs I m S fs 3 , dI fs dt 4 S fs I m (b3 ) I fs , dAfs dt b3 I fs ( d ) Afs . (1) Here, the total population N (t ) Sm (t ) I m (t ) Am (t ) S f (t ) I f (t ) Afs (t ) S m (t ) S fs (t ) I fs (t ) Afs (t ) and the parameters used in this model is defined as follows in Table 1: Table 1. Interpretation of variables and parameters Symbol Description Sm (t ), I m (t ), Am (t ) Population of susceptible, infective and AIDS-infected male individuals at time ' t ' S f (t ), I f (t ), Af (t ) Population of susceptible, infective and AIDS-infected female individuals at time 't ' S fs (t ), I fs (t ), A fs (t ) Population of susceptible, infected and AIDS-infected female sex workers at time 't ' 1 , 2 , 3 Immigration rate of susceptible male, female and female sex-workers; 1 ,2 ,3 Migration rate of susceptible male, female and female sex-workers; 1 Interaction rate of susceptible male and infected female individuals; 2 Interaction rate of susceptible male and infected female sex workers; 3 Interaction rate of susceptible female and infected male individuals; 4 Interaction rate of susceptible female sexworkers and infected male individuals; Birth rate of susceptibles and infectives in male and female populations; Natural death rate; Progression rates from HIV infective male, female and female sex-workers. b1 , b2 , b3 The flow diagram of a given model (1) is given as follows: 1 Sm Sm Sf Sf Sm ( 1 I f 2 I fs ) S m Im 2 2 1 Sfs S fs 4 S fs I m Ifs If If I fs If Im b1 I m S fs Sf 3 I m S f Im b3 I fs b2 I f Af Am 3 3 Afs ( d ) Af ( d ) Am Fig. 1 ( d ) A fs 3. Analysis of the model 3.1 Positivity and boundedness of solutions Theorem 3.1: For the time t 0, all the solutions of the system (1) are eventually confined in the compact subset {(Sm , S f , S fs , I m , I f , I fs , Am , Af , Afs ) 9 : N (Sm (t ) S f (t ) S fs (t ) I m (t ) I f (t ) I fs (t ) Am (t ) A f (t ) Afs (t )) ( ) }. ( ) Proof: Since, we have N (t ) Sm (t ) S f (t ) S fs (t ) I m (t ) I f (t ) I fs (t ) Am (t ) A f (t ) A fs (t ). Differentiating ' N (t ) ' with respect to ' t ', we get dN dSm dS f dS fs dI m dI f dI fs dAm dAf dAfs . dt dt dt dt dt dt dt dt dt dt By using (1), it becomes dN (1 2 3 ) ( Sm S f I m I fs ) ( S m S f S fs dt I m I f I fs Am Af Afs ) (1 2 3 ) d ( Am Af Afs ), it can also be written as dN ( ) N , where 1 2 3 , 1 2 3 . dt (2) Then the solution of (2) becomes Ne ( )t ( ) e( ) t c. ( ) At t 0, (3) implies N (t ) ( ) ( ) t [ N0 ]e . ( ) ( ) (3) lim Sup N As t , t ( ) . ( ) This shows that the solutions of the model (1) are bounded in the interval [0, ), i.e., confined in the region . 3.2 Disease-Free Equilibrium and the Basic Reproduction Number At the disease-free equilibrium state, I m I f I fs Am Af Afs 0. Substituting these values in the above system of equations, the disease free equilibrium of the model (1) is given by E0 (Sm0 , S 0f , S 0fs , I m0 , I 0f , I 0fs , Am0 , A0f , A0fs ) ( 1 1 2 2 3 3 , , , 0, 0, 0, 0, 0, 0). The linear stability of E0 is established by the basic reproduction number R0 and it is obtained by taking the largest Eigenvalue of the next generation matrix. The basic reproduction number R0 is the effective number of secondary infections caused by a typical infected individual during his entire period of infectiousness. Now, the next generation matrix is calculated as follows: let F be the rate of appearance of new infection corresponding to (1) and it is given as 0 1 Sm0 0 0 3 S f S0 0 F 4 fs 0 0 0 0 0 0 where S m0 1 Sm0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 , 0 0 0 (1 1 ) 0 ( 2 2 ) 0 ( 3 3 ) , Sf , S fs . ( ) ( ) Let V be the remaining transfer terms corresponding to the system (1) and it is given as follows: 0 0 0 0 0 (b1 ) 0 (b2 ) 0 0 0 0 0 0 (b3 ) 0 0 0 V . b1 0 0 ( d ) 0 0 0 b2 0 0 ( d ) 0 0 0 b3 0 0 ( d ) Now, 0 3 ( 2 2 ) ( ) (b ) 1 1 4 ( 3 3 ) FV (b1 ) 0 0 0 1 (1 1 ) ( ) (b2 ) 1 (1 1 ) 0 0 0 (b3 ) 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 . 0 0 0 0 The corresponding characteristic equation is given by det( F V 1 I ) 0, it can also be written as 1 (1 1 ) ( ) ( b2 ) 2 (1 1 ) ( ) ( b3 ) 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 3 ( 2 2 ) ( ) ( b1 ) 4 ( 3 3 ) ( b1 ) 0 0 0 Solving the above determinant (4), we get 0. (4) 2 1 3 (1 1 ) ( 2 2 ) 2 ( ) (b1 ) (b2 ) 3 0. 2 4 (1 1 ) ( 3 3 ) ( ) (b1 ) (b3 ) It can also be written as 4 2 1 3 (1 1 ) ( 2 2 ) (b3 ) ( ) ( ) ( )(b ) 2 4 1 1 3 3 2 2 ( ) ( b ) ( b ) ( b3 ) 1 2 0. Therefore, the Eigenvalues of the characteristic equation (5) are 0, 0, 0, 0 and 1 3 (1 1 ) ( 2 2 ) (b3 ) ( ) ( ) ( )(b ) 3 3 2 2 2 4 21 1 ( ) (b1 ) (b2 ) (b3 ) . Thus, the basic reproduction number R0 is given by (1 1 ){ 1 3 ( 2 2 ) (b3 ) R0 ( ) 2 4 (3 3 )(b2 )} . ( )2 (b1 ) (b2 ) (b3 ) 3.3 Existence of Endemic Equilibrium The endemic equilibrium point E1 (Sm* , S *f , S *fs , I m* , I *f , I *fs , Am* , A*f , A*fs ) is given by (1 1 ) (b1 ) I m* * ( 2 2 ) S , Sf , ( ) ( 3 I m* ) * m S *fs (3 3 ) ( 2 2 ) 3 I m* * , I , f ( 4 I m* ) ( 3 I m* ) (b2 ) I *fs (3 3 ) 4 I m* b1 I m* * , A , m ( 4 I m* ) (b3 ) ( d ) (5) A*f ( 2 2 ) 3 b2 I m* (3 3 ) 4 b3 I m* * , A . fs ( d ) ( 3 I m* ) (b2 ) ( d ) ( 4 I m* ) (b3 ) Each of the variables are positive if I m* 0. Here I m* is given by the following quadratic equation: D1 I m* 2 D2 I m* D3 0, where (6) D1 [1 3 4 (2 2 ) (b1 ) (b3 ) 2 3 4 (3 3 ) (b1 ) (b2 ) 3 4 (b1 ) (b2 ) (b3 ) ( )] 0, D2 1 3 4 (1 1 ) (2 2 ) (b3 ) 1 3 (2 2 ) (b1 ) (b3 ) 2 3 4 (1 1 ) (3 3 ) (b2 ) ( ) 2 4 (3 3 ) (b1 ) (b2 ) ( ) (b1 ) (b2 ) (b3 ){ 3 ( ) 4 }, It can also be written as D2 ( ) 2 4 (b1 ) (b2 ) (b3 ) (1 1 ){( 2 2 ) 1 3 (b3 ) ( 3 3 ) 2 3 (b2 )} 1 ( ) 2 (b1 ) (b2 ) (b3 ) 3 (b1 ) (b3 )(( 2 2 ) 1 ( )(b2 )) (3 3 ) ( ) 2 4 (b1 ) (b2 ), and D3 ( ) 2 (b1 ) (b2 ) (b3 ) (1 R02 ). For R0 1, we have D1 0, D3 0 and the first bracketed term of D2 is positive as the transmission rate of infection 4 in female sex workers is always greater than or equal to the transmission rate of infection 3 of female individuals. Hence, Descartes rule of signs suggests that there is a zero positive root of the quadratic equation (6). For R0 1, we have D1 0, D3 0 and D2 may be positive or negative. Therefore, (6) gives a unique positive root corresponding to D2 , say I m* . Thus the existence of one positive real root I m* implies the positivity of the endemic equilibrium for R0 1. 4. Stability Analysis Theorem 4.1: The disease-free equilibrium E0 of the model (1) is locally asymptotically stable when R0 1 and unstable otherwise. Proof: To prove this, suppose that Sm (t ) Sm0 A1 e t , S f (t ) S 0f A2 e t , S fs (t ) S 0fs A3 e t , I m (t ) I m0 B1 e t , I f (t ) I 0f B2 e t , I fs (t ) I 0fs B3 e t , Am (t ) Am0 C1 e t , Af (t ) A0f C2 e t , Afs (t ) A0fs C3 e t . Then, the system of equations (1) becomes ( ) A1 e t 1 (1 1 ) (1 1 ) B2 e t 2 B3 e t 0, ( ) ( ) (b1 ) B1 e t 1 (1 1 ) ( ) B2 e t 2 1 1 B3 e t 0, ( ) ( ) b1 B1 e t ( d ) C1 e t 0, ( ) A2 e t 3 3 ( 2 2 ) B1 e t 0, ( ) ( 2 2 ) B1 e t (b2 ) B2 e t 0, ( ) b2 B2 e t ( d ) C2 e t 0, ( ) A3 e t 4 4 (3 3 ) (3 3 ) B1 e t 0, B1 e t (b3 ) B3 e t 0, b3 B3 e t ( d ) C3 e t 0. (7) To study the stability criterion of DFE E0 , the Jacobian matrix M 1 has been calculated as follows: ( ) 0 0 0 M1 0 0 0 0 0 0 0 ( ) 0 0 ( ) 0 0 0 0 0 0 0 0 0 0 b1 0 0 0 0 1 (1 1 ) ( ) 2 (1 1 ) ( ) 0 0 0 0 1 (1 1 ) ( ) 2 1 1 ( ) ( ) (b2 ) 0 0 (b3 ) 0 b2 0 0 0 b3 0 3 ( 2 2 ) ( ) 4 ( 3 3 ) (b1 ) 3 ( 2 2 ) ( ) 4 ( 3 3 ) 0 0 0 0 0 0 0 0 0 . 0 0 0 0 0 0 ( d ) 0 0 0 ( d ) 0 0 0 ( d ) 0 0 0 Therefore, the first six Eigenvalues of the Jacobian determinant are , ( d ), ( d ), ( d ), ( ), ( ) and the rest of the Eigenvalues are calculated by the following cubic equation: a0 3 a1 2 a2 a3 0, where a0 1 0, a1 x y z, (8) ( ) ( ) ( ) (3 3 ) a2 x y y z z x 1 3 1 1 2 2 2 2 4 1 1 ( ) ( ) , and a3 x y z (1 R02 ). Also, x (b1 ), y (b2 ), z (b3 ). Clearly, for R0 1, we have a0 , a1 , a3 0 and a1 a2 a3 a0 is given as follows: 1 3 (1 1 ) ( 2 2 ) x ( y z) ( ) 2 a1 a2 a3 a0 ( x y ) ( ) ( 3 3 ) 2 4 1 1 ( ) ( ) (3 3 ) z x ( y z) 2 4 1 1 ( ) ( ) (3 3 ) y z ( y z) 2 4 1 1 . ( ) Hence, by using Routh-Hurwitz criterion for a third-order polynomial, since a0 , a1 , a3 0 and a1 a2 a3 a0 0 for R0 1, therefore, the roots of the cubic equation (7) have negative real parts. Thus the disease free equilibrium E0 is locally asymptotically stable for R0 1. Theorem 6.2: The endemic equilibrium E1 of the model (1) is globally asymptotically stable when R0 1. Proof: To establish the global stability of the endemic equilibrium E1 , we construct the following Lyapunov function: V ( Sm* , S *f , S *fs , I m* , I *f , I *fs ) c1 ( S m S m* S m* log S *f log Sf S * f ) c3 ( S fs S *fs S *fs log c5 ( I f I *f I *f log The time-derivative of V is given by Sf s S * fs Sm ) c2 ( S f S *f S m* ) c4 ( I m I m* I m* log If If s If I *f s ) c6 ( I fs I *fs I *fs log * ). Im ) I m* S f S *f S S * d Sm dV c1 m m c2 Sf dt S m dt S f s S *f s c3 Sf s I f I *f c5 If d Sf dt d Sf s I m I m* d I m c 4 I m dt dt I f s I *f s d If c6 Ifs dt d Ifs . dt (9) Now, by using (1) in (9), we get Sm Sm* dV c1 (1 1 Sm Sm 1 Sm I f 2 Sm I fs ) dt Sm S f S *f c2 Sf S fs S *fs ( 2 2 S f S f 3 S f I m ) c3 S fs I I* (3 3 S f 4 S fs I m ) c4 m m ( 1 Sm I f 2 Sm I fs Im I f I *f I m b1 I m I m ) c5 If I fs I *fs c6 I fs ( 3 S f I m I f b2 I f I f ) ( 4 S fs I m b3 I fs I fs ). It can also be written as S S* dV c1 m m (( ) ( Sm Sm* ) 1 Sm* I *f 2 Sm* I *fs dt Sm S f S *f 1 S m I f 2 S m I fs ) c2 Sf S fs S *fs 3 S f I m ) c2 S fs * * * (( ) ( S f S f ) 3 S f I m * * * ( ( S fs S fs ) 4 S fs I m 4 S fs I m ) (10) I *f I *fs I m I m* * * c4 1 Sm I f 2 Sm I fs I m 1 Sm * 2 Sm * Im Im I m I f I *f c5 If I fs I *fs c6 I fs 3 S f I m I f * * I 3 S f *m I f * * Im 4 S fs I m I fs 4 S fs * . I fs Thus, we have ( S f S *f )2 ( Sm Sm* )2 dV c1 ( ) c2 ( ) dt Sm Sf c3 ( S fs S *fs )2 S fs f ( x1 , x2 , x3 , x4 , x5 , x6 ), where f ( x1 , x2 , x3 , x4 , x5 , x6 ) (c1 c4 ) 1 a x1 x5 (c1 c4 ) 2 d x1 x6 (c2 c5 ) 3 b x2 x4 (c3 c4 ) 4 c x3 x4 (c1 1 a c5 3 d ) x5 (c1 2 d c6 4 c) x6 (c2 3 b c3 4 c c4 1 a c4 2 d ) x4 1 1 (c1 1 a c1 2 d ) 1 c2 3 b 1 x1 x2 x x 1 c3 4 c 1 c4 1 a 1 1 5 c4 2 d x3 x4 x3 x4 x2 x4 x1 x6 c5 3 b 1 1 c6 4 c 1 x4 x6 x5 Also, Sf S fs If I fs Sm I x1 , * x2 , * x3 , m* x4 , * x5 , * x6 , * Sm Sf S fs Im If I fs Sm* I *f a, S *f I m* b, S *fs I m* c, Sm* I *fs d . . (12) To determine c1 , c2 , c3 , c4 , c5 , c6 , we set the coefficients of x1 x5 , x1 x6 , x2 x4 , x3 x4 , x5 , x6 , x4 equal to zero and solving these resulting equations, we have c1 c4 , c2 c5 and c3 c6 . Hence, by using these results in (10) and taking c1 c4 1, we get ( S f S *f )2 ( Sm Sm* )2 dV c1 ( ) c2 ( ) dt Sm Sf c3 ( S fs S *fs )2 S fs 1 1 x x x x 1 a 4 1 5 2 4 x1 x2 x4 x5 1 1 x x x x 2 d 4 1 6 3 4 0. x1 x3 x4 x6 dV dV 0 in the region and the inequality 0 holds only if dt dt x1 x2 x3 x4 x5 x6 1, for which S m S m* , S f S *f , S fs S *fs , I m I m* , I f I *f , I fs I *fs . Thus, it implies Thus, by LaSalle’s invariance principle, the unique endemic equilibrium E1 of the model (1) is globally asymptotically stable for R0 1. 5. Numerical Analysis In this section, the system (1) is presented graphically when all the parameters are constant and are the following values: 1 80; 2 60; 3 50; 1 0.00005; 2 0.0002; 3 0.0001; 4 0.0003; b1 0.107261; b2 0.0924; b3 0.25; 0.0743; d 0.123; 0.03. Fig. 2 Population versus time Conclusion In the present communication, a nonlinear mathematical model is developed to examine the transmission of HIV/AIDS with the influence of role of female sex workers. Also, study the effect of immigration and emigration of susceptible male, female and female sex workers. By analyzing the model, we find that the disease free equilibrium is globally asymptotically stable for the basic reproduction number is less than unity and the endemic equilibrium is globally stable for the basic reproduction number is greater than unity. References 1. Anderson, R.M. (1988), The role of mathematical models in the study of HIV transmission and the epidemiology of AIDS, Journal of Acquired Immune Deficiency Syndrome, 1, pp. 214 – 256. 2. Anderson, R.M., May, R.M., 1979, Population Biology of Infectious Diseases I, Nature, 280, pp. 361-367. 3. Anderson, R.M., May, R.M., 1991, Infectious Disease of Humans: Dynamics and Control, Oxford University Press, Oxford, pp. 1-757. 4. Baral, S., Beyrer, C., Muessig, K., Poteat, T., Wirtz A.L., Decker, M.R., Sherman, S.G. and Kerrigan, D., (2012). Burden of HIV among female sex workers in low-income and middle-income countries: a systematic review and meta-analysis. Lancet Infectious Diseases, 12, pp. 538-549. 5. Bhunu, C.P., Mushayabasa, S., (2012). Prostitution and drug (alcohol) misuse: the menacing combination, Journal of Biological Systems, 20(2), pp. 177–193. 6. Daabo, M. I., Seidu, B., (2012). Modeling the Effect of Irresponsible Infective Immigrants on the Transmission Dynamics of HIV/AIDS. Advances in Applied Mathematical Biosciences, 3(1), pp. 31-40. 7. Hethcote, H.W., (2000). The mathematics of infectious diseases. Society for the Industrial and Applied Mathematics, 42(4), pp. 599-653. 8. Hethcote, H.W., Mena-Lorca, J., (1992). Dynamic models of infectious diseases as regulators of population sizes. Journal of Mathematical Biology, 30, pp. 693-716. 9. http://www.unaids.org/en/resources/campaigns/World-AIDS-Day-Report-2014/factsheet. 10. http://www.who.int/hiv/medicentre/2006EpiUpdateen.pdf. 11. http://www.who.int/tb/hiv/en/. 12. Jacquez, J.A., Simon, C.P., Koopman, J., Sattenspiel, L., Perry T., (1988). Modeling and analyzing HIV transmission: the effect of contact patterns. Mathematical Biosciences, 92, pp. 119-199. 13. Kaur, N., Ghosh, M., Bhatia, S. S., (2014), Mathematical Analysis of the Transmission Dynamics of HIV/AIDS: Role of Female Sex Workers. Applied Mathematics & Information Sciences, 8(5), pp. 2491-2501. 14. Molaei, M.R., (2010). A mathematical model for an epidemic in an open society. Studia Universitatis Babes-Bolyai, Biologia, 1, pp. 61-65. 15. Morison, L., Weiss, H.A., Buv, A., Caral, M., Abega, S.C., Kaona, F., Kanhonou, L., Chege, J. and Hayes, R.J., (2001). Commercial sex and the spread of HIV in four cities in sub-Saharan Africa. AIDS, 15, pp. 61-69. 16. Naresh, R., Omar S., (2003). Analysis of a nonlinear AIDS epidemic model with standard incidence. International Journal of Physical Sciences, 15, 63-70. 17. Rao, A.S., Thomas, K., Sudhakar, K., Maini, P.K., (2009). HIV/AIDS epidemic in India and predicting the impact of the national response: mathematical modeling and analysis. Mathematical Biosciences and Engineering, 6 (4), pp. 779-813. 18. Srinivasa Rao, A.S.R., (2003). Mathematical modeling of AIDS epidemic in India, Current Science, 84, 1192-1197. 19. Thappa, D.M., Singh, N., Kaimal, S., (2007). Prostitution in India and its role in the spread of HIV infection. Indian Journal of Sexually Transmitted Diseases, 28(2), pp. 69– 75. 20. UNAIDS/WHO, AIDS epidemic update, 2009. 21. Venkataramana, C. B. S., & Sarada, P. V., (2001). Extent and speed of spread of HIV infection in India through the commercial sex networks: a perspective, Tropical Medicine and International Health, 6, 1040-1061.