Download Angle-Side-Angle Triangle Congruence

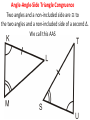
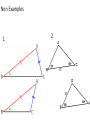
5.6 - AAS ASA HL Part 2
Obj: Proving Triangle Congruence
Angle-Side-Angle (ASA)
Angle-Angle-Side (AAS)
Hypotenuse-Leg (HL)
Review
An included angle is the
angle between two given
sides.
An included side is the
side between two given
angles.
Angle-Side-Angle Triangle Congruence
Two angles & the included side are ≅ to the two
angles & the included side of a second Δ.
We call this ASA
Angle-Angle-Side Triangle Congruence
Two angles and a non-included side are ≅ to
the two angles and a non-included side of a second Δ.
We call this AAS
Hypotenuse-Leg Triangle Congruence
***This only works for right triangles***
The hypotenuse & leg of a right Δ are ≅
the hypotenuse & leg of the 2nd right Δ.
We call this HL
A.S.S. Theorem (Non-Right Triangles)
Given that an angle followed by two consecutive
sides is ≅ to the same of a 2nd Δ is not enough to
prove the two triangles are congruence for nonright triangles. We call this the donkey theorem.
A.S.S. Theorem (Non-Right Triangles)
Given an angle followed by two consecutive sides is
not enough to prove triangle congruence for nonright triangles. As you can see, ΔLMP ΔLMP.
P
P
L
M
mPLM = 59.95
LM = 6.01 cm
MP = 5.75 cm
L
M
mPLM = 59.95 Angle
LM = 6.01 cm
MP = 5.75 cm
Side
Side
Examples: Determine if the triangles are
congruent. How do you know?
1
3
2
Non Examples
1
2
Triangle congruence statement. When you
state two triangles to be congruent
(ΔABC ≅ ΔDEF),
you want to check that each of the following
six congruence statements are true.
∠A≅∠D
∠B≅∠E
∠C≅∠F
𝐴𝐵 ≅ 𝐷𝐸
𝐵𝐶 ≅ 𝐸𝐹
𝐴𝐶 ≅ 𝐷𝐹