Download RANDOM VARIABLES AND THEIR DISTRIBUTIONS

STATISTICS 3031 – THE POISSON DISTRIBUTION
The Poisson random variable has the range {0,1, 2, 3, } and its probability distribution is given by
e   x
, for x  0,1, 2, 3,
p( x ) 
x!
, where   0 is the parameter of the distribution.
It can be shown that these Poisson probabilities sum to 1 as an infinite series.
For x  0,1, 2, and 3, p(0)  e  , p(1)  e   , p(2) 
e   2
e   3
, p(3) 
.
2
6
The graph of this distribution is skewed to the right and the probabilities approach zero as x goes
to infinity. The graph has its maximum value at x = the largest integer   ; in particular, if  is an
integer, then the graph has its maximum value at  .
The Poisson distribution has mean    and variance 2   .
The Poisson distribution is used as a building block in many complex probability models called
stochastic processes. For example, it can be used to approximate the number of “events” that
occur at random in a finite interval of time or in a bounded region of two-dimensional or threedimensional space. For example, the number of new cases of whooping cough in children in a
randomly selected three-month period might have a Poisson distribution. The number of gopher
holes in a randomly selected square yard of ground in a meadow might be Poisson distributed.
Another application of the Poisson is to approximate Binomial probabilities. It can be shown that
if X has a Binomial distribution with parameters n and p and if n is large and p is close to 0, then
X will be approximately Poisson with parameter   np . The approximation is excellent if n  100
and   10 .
For example, if n = 100 and p = .02, then   100(.02)  2 .
 100 
The exact Binomial probability is P ( X  4)  
(.02)4 (.98)96  .09021 .

 4 
e 2 24
 .09022 . The approximation is
The approximating Poisson probability is P ( X  4) 
4!
excellent.
This Poisson approximation to the Binomial is useful when the Binomial parameters n and p are
not known but n is known to be large and p is known to be small. The strategy is to estimate the
mean   np from some data and then to use the Poisson distribution with parameter    .
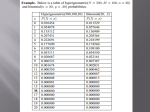
Example: Suppose that it is estimated that an average of 8 people die of rabies every 10 years.
Let X be the number of people who die of rabies in a randomly selected 10-year period. Assume
the usual Binomial conditions for X where success is that a person dies of rabies in this period, n
is the number of people exposed to the risk of dying from rabies, and p is the probability that a
person will die of rabies. Now n and p are both unknown, but it is clear that n must be large and p
must be small. Furthermore, the mean of X is   np  8 . Hence, X must be approximately
Poisson with parameter   8 .