* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Ohio Content Standards
History of geometry wikipedia , lookup
Noether's theorem wikipedia , lookup
Rational trigonometry wikipedia , lookup
Multilateration wikipedia , lookup
Trigonometric functions wikipedia , lookup
Euclidean geometry wikipedia , lookup
History of trigonometry wikipedia , lookup
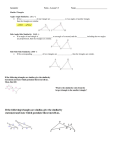
Lesson 6-3 Similar Triangles Ohio Content Standards: Ohio Content Standards: Describe and apply the properties of similar and congruent figures; and justify conjectures involving similarity and congruence. Ohio Content Standards: Make and test conjectures about characteristics and properties (e.g., sides, angles, symmetry) of twodimensional figures and threedimensional objects. Ohio Content Standards: Use proportions in several forms to solve problems involving similar figures (part-to-part, part-to-whole, corresponding sides between figures). Ohio Content Standards: Use proportional reasoning and apply indirect measurement techniques, including right triangle trigonometry and properties of similar triangles, to solve problems involving measurements and rates. Ohio Content Standards: Apply proportional reasoning to solve problems involving indirect measurements or rates. Postulate 6.1 Angle-Angle (AA) Similarity Postulate 6.1 Angle-Angle (AA) Similarity If the two angles of one triangle are congruent to two angles of another triangle, then the triangles are similar. Theorem 6.1 Side-Side-Side (SSS) Similarity Theorem 6.1 Side-Side-Side (SSS) Similarity If the measures of the corresponding sides of two triangles are proportional, then the triangles are similar. Theorem 6.2 Side-Angle-Side (SAS) Similarity Theorem 6.2 Side-Angle-Side (SAS) Similarity If the measures of two sides of a triangle are proportional to the measures of two corresponding sides of another triangle and the included angles are congruent, then the triangles are similar. In the figure, AB DC , BE 27, DE 45, AE 21, and CE 35. Determine which tria ngles in the figure are similar. C B E A D Given RS UT , RS 4, RQ x 3, QT 2 x 10, UT 10, find RQ and QT . 4 R x+3 S Q 2x + 10 U 10 T Josh wanted to measure the height of the Sears Tower in Chicago. He used a 12-foot light pole and measured its shadow at 1 p.m. The length of the shadow was 2 feet. Then he measured the length of the Sears Tower’s shadow and it was 242 feet at that time. What is the height of the Sears Tower? Assignment: Pgs. 302-306 10-20 evens, 51-61 odds