Download efficient algorithms for mining arbitrary shaped clusters

EFFICIENT ALGORITHMS FOR MINING ARBITRARY
SHAPED CLUSTERS
By
Vineet Chaoji
A Thesis Submitted to the Graduate
Faculty of Rensselaer Polytechnic Institute
in Partial Fulfillment of the
Requirements for the Degree of
DOCTOR OF PHILOSOPHY
Major Subject: COMPUTER SCIENCE
Approved by the
Examining Committee:
Dr. Mohammed J. Zaki, Thesis Adviser
Dr. Boleslaw Szymanski, Member
Dr. Mark Goldberg, Member
Dr. Malik Magdon-Ismail, Member
Dr. Taneli Mielikäinen, External Member
Rensselaer Polytechnic Institute
Troy, New York
July 2009
(For Graduation August 2009)
c Copyright 2009
by
Vineet Chaoji
All Rights Reserved
ii
CONTENTS
LIST OF TABLES . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
v
LIST OF FIGURES . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
vi
ACKNOWLEDGMENT . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
ix
ABSTRACT . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
xi
1. Introduction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1
1.1
Clustering – Application Domains . . . . . . . . . . . . . . . . . . . .
2
1.2
Shape-based Clustering . . . . . . . . . . . . . . . . . . . . . . . . . .
3
1.2.1
Motivating Applications . . . . . . . . . . . . . . . . . . . . .
4
1.2.2
Problem Formulation and Contribution . . . . . . . . . . . . .
6
Thesis Outline . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
9
1.3
2. Background and Related Work . . . . . . . . . . . . . . . . . . . . . . . . . 10
2.1
2.2
2.3
Clustering Preliminaries . . . . . . . . . . . . . . . . . . . . . . . . . 10
2.1.1
Data Types . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10
2.1.2
Distance Measures . . . . . . . . . . . . . . . . . . . . . . . . 10
Dominant Clustering Paradigms . . . . . . . . . . . . . . . . . . . . . 12
2.2.1
Differentiating Properties
. . . . . . . . . . . . . . . . . . . . 12
2.2.2
Categorization . . . . . . . . . . . . . . .
2.2.2.1 Partitional Clustering . . . . .
2.2.2.2 Hierarchical Clustering . . . . .
2.2.2.3 Probabilistic/fuzzy Clustering .
2.2.2.4 Graph-theoretic Clustering . .
2.2.2.5 Grid-based Clustering . . . . .
2.2.2.6 Evolution and Neural-net based
. . . . . .
. . . . . .
. . . . . .
. . . . . .
. . . . . .
. . . . . .
Clustering
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
14
14
17
19
19
20
20
Review of Shape-based Clustering Methods . . . . . . . . . . . . . . . 22
2.3.1
Density-based Clustering . . . . . . . . . . . . . . . . . . . . . 22
2.3.2
Hierarchical Clustering . . . . . . . . . . . . . . . . . . . . . . 23
2.3.3
Spectral Clustering . . . . . . . . . . . . . . . . . . . . . . . . 26
2.3.4
SPARCL – Brief Overview . . . . . . . . . . . . . . . . . . . . 29
2.3.5
Backbone based Clustering – An Overview . . . . . . . . . . . 29
iii
3. SPARCL: Efficient Shape-based Clustering . . . . . . . . . . . . . . . . . . 31
3.1
The SPARCL Algorithm . . . . . . . . . . . . . . . . . . . . . . . . . 32
3.2
Phase 1 – Kmeans Algorithm . . . . . . . . . . . . . . . . . . . . . . 33
3.3
3.2.1
Kmeans Initialization Methods . . . . . . . . . . . . . . . . . 34
3.2.2
Initialization using Local Outlier Factor . . . . . . . . . . . . 37
3.2.3
Complexity Analysis of LOF Based Initialization . . . . . . . 38
Phase 2 – Merging Neighboring Clusters . . . . . . . . . . . . . . . . 40
3.3.1
Cluster Similarity . . . . . . . . . . . . . . . . . . . . . . . . . 40
3.4
Complexity Analysis . . . . . . . . . . . . . . . . . . . . . . . . . . . 43
3.5
Estimating the Value of K . . . . . . . . . . . . . . . . . . . . . . . . 44
3.6
Experiments and Results . . . . . . . . . . . . . . . . . . . . . . . . . 48
3.7
3.6.1
Datasets . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 49
3.6.1.1 Synthetic Datasets . . . . . . . . . . . . . . . . . . . 49
3.6.1.2 Real Datasets . . . . . . . . . . . . . . . . . . . . . . 49
3.6.2
Comparison of Kmeans Initialization Methods . . . . . . . . . 50
3.6.3
Results
3.6.3.1
3.6.3.2
3.6.3.3
3.6.3.4
3.6.3.5
3.6.4
Results on Real Datasets . . . . . . . . . . . . . . . . . . . . . 62
3.6.5
Comparison with Locally Linear Embedding . . . . . . . . . . 63
on Synthetic Datasets . . . . . . .
Scalability Experiments . . . . .
Clustering Quality . . . . . . . .
Varying Number of Clusters . . .
Varying Number of Dimensions .
Varying Number of Seed-Clusters
. . .
. . .
. . .
. . .
. . .
(K)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
50
54
56
58
59
61
Conclusions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 64
4. Shape-based Clustering through Backbone Identification . . . . . . . . . . 67
4.1
Related Techniques . . . . . . . . . . . . . . . . . . . . . . . . . . . . 68
4.1.1
4.2
4.3
Skeletonization . . . . . . . . . . . . . . . . . . . . . . . . . . 69
The Clustering Algorithm . . . . . . . . . . . . . . . . . . . . . . . . 71
4.2.1
Preliminaries . . . . . . . . . . . . . . . . . . . . . . . . . . . 71
4.2.2
Phase 1 – Backbone Identification . . . . . . . . . . . . . . . . 72
4.2.2.1 Minimum Description Length principle . . . . . . . . 78
4.2.3
Phase 2 – Cluster Identification . . . . . . . . . . . . . . . . . 81
4.2.4
Complexity Analysis . . . . . . . . . . . . . . . . . . . . . . . 83
Experimental Evaluation . . . . . . . . . . . . . . . . . . . . . . . . . 83
iv
4.4
4.3.1
Datasets . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 84
4.3.2
Scalability Results . . . . . . . . . . . . . . . . . . . . . . . . 84
4.3.3
Clustering Quality Results . . . . . . . . . . . . . . . . . . . . 85
4.3.4
Parameter Sensitivity Results . . . . . . . . . . . . . . . . . . 86
Conclusion . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 87
4.4.1
Comparison with SPARCL . . . . . . . . . . . . . . . . . . . . 88
5. Conclusion and Future Work . . . . . . . . . . . . . . . . . . . . . . . . . . 91
5.1
Efficient Subspace Clustering
. . . . . . . . . . . . . . . . . . . . . . 91
5.2
Shape Indexing . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 92
v
LIST OF TABLES
2.1
Summary of spatial (shape-based) Clustering Algorithms . . . . . . . . 27
3.1
Comparison on synthetic datasets. The distortion scores are shown for
each method. The value in bold indicate the best result for each row. . 51
3.2
Runtime Performance on Synthetic Datasets. All times are reported in
seconds. ‘-’ for DBSCAN and Spectral method denotes the fact that it
ran out of memory for all these cases. . . . . . . . . . . . . . . . . . . . 51
4.1
Scalability results on dataset with 13 true clusters. The size of the
dataset is varied keeping the noise at 5% of the dataset size. . . . . . . 86
vi
LIST OF FIGURES
1.1
Applications of Shape-based Clustering in Image Analysis, Geographical Information Systems and Sensor Data. . . . . . . . . . . . . . . . . .
5
2.1
Contingency Table for Jaccard Co-efficient . . . . . . . . . . . . . . . . 11
2.2
Taxonomy of Clustering Algorithms . . . . . . . . . . . . . . . . . . . . 15
2.3
The k-means Algorithm . . . . . . . . . . . . . . . . . . . . . . . . . . . 17
2.4
DBScan – Density reachability, core points and noise points. minPts = 2 22
2.5
CHAMELEON Clustering Steps. Figure from [64] . . . . . . . . . . . . 24
2.6
CHAMELEON – Relative Interconnectivity. Figure from [64]. . . . . . . 25
2.7
CHAMELEON – Relative Closeness. Figure from [64]. . . . . . . . . . . 26
3.1
The SPARCL Algorithm . . . . . . . . . . . . . . . . . . . . . . . . . . 32
3.2
Effect of Choosing mean or actual data point . . . . . . . . . . . . . . . 34
3.3
Bad Choice of Cluster Centers . . . . . . . . . . . . . . . . . . . . . . . 35
3.4
Local Outlier Based Center Selection . . . . . . . . . . . . . . . . . . . 39
3.5
Projection of points onto the vector connecting the centers . . . . . . . 40
3.6
Estimating the value of K . . . . . . . . . . . . . . . . . . . . . . . . . 46
3.7
Generating seed representatives with cdistmin . . . . . . . . . . . . . . . 47
3.8
Sensitivity Comparison: LOF vs. Random . . . . . . . . . . . . . . . . 51
3.9
SPARCL clustering on standard synthetic datasets from the literature. . 52
3.10
Results on Swiss-roll
3.11
Scalability Results on Dataset DS5
3.12
Clustering Quality on Dataset DS5 . . . . . . . . . . . . . . . . . . . . 55
3.13
Clustering Results on 3D Dataset . . . . . . . . . . . . . . . . . . . . . 56
3.14
Clustering quality for varying dataset size . . . . . . . . . . . . . . . . . 58
3.15
Varying Number of Natural Clusters . . . . . . . . . . . . . . . . . . . . 59
. . . . . . . . . . . . . . . . . . . . . . . . . . . . 53
vii
. . . . . . . . . . . . . . . . . . . . 54
3.16
Varying Number of Dimensions . . . . . . . . . . . . . . . . . . . . . . . 60
3.17
10 dimensional dataset (size=500K, k=10) projected onto a 3D subspace 61
3.18
Clustering quality for varying number of seed-clusters . . . . . . . . . . 61
3.19
Protein Dataset . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 62
3.20
Cluster separation with Locally Linear Embedding . . . . . . . . . . . . 63
3.21
Cancer Dataset: (a)-(c) are the actual benign tissue images. (d)-(f)
gives the clustering of the corresponding tissues by SPARCL. . . . . . . 66
4.1
Initial dataset (4.1(a)); after iterations 3 and 6; and the backbone after
8 iterations (right) of the algorithm . . . . . . . . . . . . . . . . . . . . 68
4.2
Example skeleton of a binary image (in black). The white outline is the
skeleton. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 70
4.3
Sample dataset showing one iteration of glob and movement . . . . . . 72
4.4
k-NN matrices for sample dataset . . . . . . . . . . . . . . . . . . . . . 72
4.5
Bubble plot for Figure 4.1(d). The size of a bubble is proportionate to
the weight wi of a point. . . . . . . . . . . . . . . . . . . . . . . . . . . 74
4.6
The Backbone Identification Based Clustering Algorithm . . . . . . . . 74
4.7
Example illustrating the globbing-movement twin process. . . . . . . . . 76
4.8
Reconstructed (and original) k-NN matrices for sample dataset . . . . . 77
4.9
The number of points moved and globbed per iteration for a dataset
with 1000K points. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 80
4.10
Balancing the two contradicting influences in the clustering formulation. 81
4.11
Scalability Results for Backbone Based Clustering . . . . . . . . . . . . 85
4.12
Backbone/skeleton of 2D synthetic datasets in our study. Left column:
original dataset, right column: skeletons. . . . . . . . . . . . . . . . . . 87
4.13
Backbone/skeleton of 3D synthetic datasets in our study. Left column:
original dataset, right column: skeletons. . . . . . . . . . . . . . . . . . 88
4.14
Purity score with varying dataset size . . . . . . . . . . . . . . . . . . . 89
4.15
Execution time and purity for varying number of nearest neighbors . . . 89
5.1
Subspace clustering – Challenges for SPARCL . . . . . . . . . . . . . . 91
5.2
Local Outlier Factor based representatives are rotation invariant. . . . . 93
viii
ACKNOWLEDGMENT
While I think back about the interesting graduate school years at RPI, this journey
would not have been anywhere close, had it not been for the following people.
First and foremost, I sincerely thank my adviser, Professor Zaki for his support,
both in research and otherwise. He has this amazing style of advising – giving
freedom but at the same time questioning; helping us to think but not hand-holding;
being gently pushy but never overbearing; acknowledging lack of progress but still
being optimistic. Above all, he has been very approachable and always willing to
discuss ideas. I have enjoyed many involved discussions in his office. I am extremely
fortunate to have had him as my adviser, otherwise my frequent India trips to meet
my wife would not have been possible :)
I would also like to thank my committee members, Professor Goldberg and Professor
Magdon-Ismail, for agreeing to be a part of my committee. Their courses during
graduate school were the most informative. Professor Magdon-Ismail gave very good
suggestions and ideas during my candidacy and beyond.
I have had the opportunity of working with the remaining members of my committee
on other projects. I thank Professor Szymanski for allowing me to be associated
with the RDM project after my active participation ended. Meetings with Professor
Szymanski have always been very exciting – full of good research ideas sprinkled
with anecdotes from history, literature and science. It was a pleasure interacting
with him.
Apart from agreeing to be a part of my committee, I have many things to thank
Taneli for. He was a wonderful mentor when I interned at Nokia Research Center
over Summer 2008. I had a fruitful and a memorable summer. He also provided
multiple opportunities for me to continue my association with Nokia Research. I
am very grateful to him for those opportunities and look forward to his guidance
and mentorship further ahead in my career.
Huge thanks goes to Terry Hayden and Chris Coonrad. They are the pillars of
the department. Because of their efforts, graduate life in the department seems so
ix
comfortable. I will miss those csgrads mails from Chris and Terry :)
A large part of graduate life is spend in the lab with fellow graduate students. I
have my fondest memories at RPI with my labmates and colleagues. I have enjoyed
working with Hasan and Saeed on many projects. In particular, Hasan’s enthusiasm
while working on a project has been contagious. We discussed many ideas and Hasan
always had thought provoking insight. Apart from research related aspects, I have
seen (and try to imbibe) the merits of tremendous hard-work and perseverance from
Hasan. Saeed has the knack of grasping new concepts and building on those. It was
fun working with him on designing the experiments for the ORIGAMI and the
SPARCL papers. I owe a lot of my awareness of world politics to Saeed :) I would
also like to acknowledge a few other colleagues/friends – Asif, Ali, Apirak, Hilmi,
Krishna and Medha.
Last but most important, I owe a lot to my family members. Without their collective
support obtaining this degree would have been much more difficult. I am indebted
to my wife, Anjali, who stood by me throughout these years. She was pushy at
times but always very understanding and supportive. Credit goes to my immediate
family members – my parents and sister (Aai, Baba and Priti), and Anjali’s parents
and sister (Mom, Dad and Neha) for their constant support.
This thesis is dedicated to Ajoba (my grandfather), who passed away on the day of
my candidacy. Apart from being the first one to have a PhD in my family, he has
been a great source of inspiration for me. He was always very curious about my
research and its progress.
x
ABSTRACT
Clustering is one of the fundamental data mining tasks. Many different clustering
paradigms have been developed over the years, which include partitional, hierarchical, mixture model based, density-based, spectral, subspace, and so on. Traditional
algorithms approach clustering as an optimization problem, wherein the objective is
to minimize certain quality metrics such as the squared error. The resulting clusters
are convex polytopes in d-dimensional metric space. For clusters that have arbitrary shapes, such a strategy does not work well. Clusters with arbitrary shapes
are observed in many areas of science. For instance, spatial data gathered from
Geographic Information Systems, data from weather satellites, data from studies on
epidemiology and sensor data rarely possess regular shaped clusters. Image segmentation is an area of technology that deals extensively with arbitrary shaped regions
and boundaries. In addition to the complex shapes some of the above applications
generate large volumes of data. The set of clustering algorithms that identify irregular shaped clusters are referred to as shape-based clustering algorithms. These
algorithms are the focus of this thesis.
Existing methods for identifying arbitrary shaped clusters include density-based,
hierarchical and spectral algorithms. These methods suffer either in terms of the
memory or time complexity, which can be quadratic or even cubic. This shortcoming has restricted these algorithms to datasets of moderate sizes. In this thesis we
propose SPARCL, a simple and scalable algorithm for finding clusters with arbitrary
shapes and sizes. SPARCL has a linear space and time complexity. SPARCL consists of two stages – the first stage runs a carefully initialized version of the Kmeans
algorithm to generate many small seed clusters. The second stage iteratively merges
the generated clusters to obtain the final shape-based clusters. The merging stage
is guided by a similarity metric between the seed clusters. Experiments conducted
on a variety of datasets highlight the effectiveness, efficiency, and scalability of our
approach. On large datasets SPARCL is an order of magnitude faster than the
best existing approaches. SPARCL can identify irregular shaped clusters that are
xi
full-dimensional, i.e., the clusters span all the input dimensions.
We also propose an alternate algorithm for shape-based clustering. In prior clustering algorithms the objects remain static whereas the cluster representatives are
modified iteratively. We propose an algorithm based on the movement of objects
under a systematic process. On convergence, the core structure (or the backbone) of
each cluster is identified. From the core, we can identify the shape-based clusters
more easily. The algorithm operates in an iterative manner. During each iteration,
a point can either be subsumed (the term “globbing” is used in this text) by another
representative point and/or it moves towards a dense neighborhood. The stopping
condition for this iterative process is formulated as a MDL model selection criterion.
Experiments on large datasets indicate that the new approach can be an order of
magnitude faster, while maintaining clustering quality comparable with SPARCL.
In the future, we plan to extend our work to identify subspace clusters. A subspace
cluster spans a subset of the dimensions in the input space. The task of subspace
clustering thus involves not only identifying the cluster members, but also the relevant dimensions for each cluster. Indexing spatial objects using the seed selection
approach proposed in SPARCL is another line of work we intend to explore.
xii
CHAPTER 1
Introduction
Clustering has been a traditional and a prominent area of research within the data
mining, machine learning and statistical learning communities. Along with classification and regression, cluster analysis covers most techniques proposed in these
communities. The growing interest in the field of cluster analysis is fueled by a large,
constantly growing, set of applications that have benefited greatly by the progress
in this area.
Broadly, clustering can be defined as follows. Given a set D of n objects in
d-dimensional space, cluster analysis assigns the objects into k groups such that
each object in a group is more similar to other objects in its group as compared
to objects in other groups 1 . While some clustering algorithms merely identify
members of different groups, others also provide the characteristic representative(s)
for each group. Some other algorithms are able to identify isolated objects that
do not belong to any specific group. These objects are atypical and are commonly
known as outliers or noise. Another class of clustering algorithms assigns each
object a probability of belonging to each of the k groups. A more thorough review
of clustering paradigms appears in Section 2.2.
Within the machine learning community, cluster analysis is popularly known
as unsupervised learning. Unsupervised learning derives its name from the complementary field of supervised learning, popularly known as classification. On one
hand, the classification task is aided (or supervised) by the presence of labels for
the objects and the goal is to assign labels to new unseen objects. On the contrary,
cluster analysis is devoid of any such supervision. Hence the name unsupervised
learning. On a related note, techniques that combine both supervised and unsupervised learning have also been studied within the machine learning community. They
are aptly known as semi-supervised learning algorithms.
In this thesis, we focus on clustering algorithms that can capture clusters of
1
This is a very general definition. Variations and specialization of this definition can be seen
for different flavors of clustering problems.
1
2
arbitrary shapes and sizes. These algorithms are commonly known in the literature
as spatial clustering algorithms, although we mostly refer to them as shape-based
clustering algorithms. Throughout this document, objects will be interchangeably
referred to as data points or instances. Similarly, the groups will be referred to
as clusters and terms ‘cluster analysis’ and clustering will be used interchangeably.
The d dimensions will be called as the features or attributes of the objects.
1.1
Clustering – Application Domains
This notion of capturing similarity between objects lends itself to a variety of
applications. As a result, cluster analysis plays an important role in almost every
area of science and engineering, including bioinformatics [55], market research [96],
privacy and security [62], image analysis [105], web search [125], health care [89]
and many others. Some of the key application domains of clustering are described
in this section.
Market Research: Cluster analysis is widely used in market research [118, 102].
Researchers have used cluster analysis to group or segment populations/customers.
Such a segmenting can help gain useful insight into market penetration, customer
base size and product positioning [117]. Moreover, the result of cluster analysis can
also reveal the correlations between the various segments. For market surveys and
test panels, cluster analysis can help determine the size and composition of test
markets [30].
Finance: As market research is crucial for new product developers, a good understanding of stocks is important for brokers/traders [41]. Grouping related stock
options helps traders plan their hedging strategy. Similarly, knowledge of related
stocks can help infer similar behavior under different market conditions [87]. Studies have been conducted using cluster analysis to understand regional differences in
market behavior [17].
Customer profiling: Increased availability of customer behavior data (online purchases, website visits, reviews, comments, wish lists, etc.) has made it possible to
build models to capture customer preferences [24]. Customer profiling has enabled
organizations to not only provide targeted products (and recommendations) but also
3
superior customer service. Analyzing customer data has also helped financial institutes and online stores identify fraudulent behavior [51]. Within clinical research,
grouping patient symptoms and diagnoses has helped health care practitioners identify diseases effectively.
Planning and governance: Identifying population dynamics enables authorities
to better distribute facilities (schools, hospitals, etc.) across a town or city. Similarly, spread of diseases can also be contained based on identification of normal and
“abnormal” clusters [86].
Sciences: Within the scientific computing community, clustering has been used by
astronomers to categorize constellations and stars [60]. Interesting problems in life
sciences have also applied cluster analysis. Grouping protein sequences [78], analysis of gene expression data [27] and building the phylogenetic tree [85] are a few
examples.
Internet-based Applications: Internet based applications such as search (both
image and text) [16], books and movie recommendations, and music portals have
effectively utilized cluster analysis to provide improved and customized results.
Miscellaneous: Other application within computer science include detecting communities in social network graphs [113], image segmentation [105] and grouping
related documents [109].
The set of applications described above clearly indicate that clustering is one
of the major data mining methods. Despite the vast amount of research in this area,
the emergence of new applications creates the need for more effective and efficient
clustering algorithms.
1.2
Shape-based Clustering
In this thesis, our focus is on the arbitrary-shape clustering task. We use the
term shape-based clustering for all algorithmic techniques that capture clusters with
arbitrary shapes, varying densities and sizes. Shape-based clustering remains of
active interest, and several previous approaches have been proposed; spectral [105],
density-based (DBSCAN [34]), and nearest-neighbor graph based (Chameleon [64])
approaches are the most successful among the many shape-based clustering methods.
4
However, they either suffer from poor scalability or are very sensitive to the choice of
the parameter values. On the one hand, simple and efficient algorithms like Kmeans
are unable to mine arbitrary-shaped clusters, and on the other hand, clustering
methods that can cluster such datasets are not very efficient. Considering the volume
of data generated by current sources (e.g., geo-spatial satellites) there is a need for
efficient algorithms in the shape-based clustering domain that can scale to much
larger datasets.
1.2.1
Motivating Applications
The need for spatial clustering can be illustrated from the following histor-
ical incident. Figure 1.1(a)2 shows the map of London during the 1855 Cholera
outbreak. The map marks the location of deaths caused due to cholera and the
position of water pumps. The story goes that Dr. John Snow (one of the founders
of medical epidemiology) used the map to correlate the deaths with the sources of
water. Grouping/clustering the occurrences of deaths, along with the location of
the pumps helped him identify the pump with contaminated water. Although this
is a small example and at that time techniques from the field of cartology were more
popular as compared to cluster analysis; even then this goes to emphasis the role of
shape-based clustering in modern day Geographic Information Systems.
Astronomy-related studies, research on epidemiology, location based applications, seismological observations are a few sources of spatial data. Improvements in
sensor devices, observation satellites and GPS devices have enabled gathering finer
and varied types of data, resulting in a large volume of gathered data. Identifying
shape-based clusters could aid in resource allocation, urban planning and marketing,
health care and criminology. Some recent applications of spatial data and clustering
are outlined below.
Location-based Search: With the popularity of Google Local, Ovi Maps from
Nokia, Placemaker from Yahoo and similar location specific services, efficient algorithms for indexing and querying spatial data have come to the forefront. Efficient
response to spatial queries such as “Find all restaurants in the vicinity of Empire
2
Image taken from http://en.wikipedia.org/wiki/GIS
5
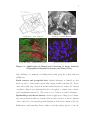
(a) GIS Data – London Cholera
(b) Image of Katrina Hurricane
(c) Satellite Image of California Forest Fire
(d) Chromosome Separation
Figure 1.1: Applications of Shape-based Clustering in Image Analysis,
Geographical Information Systems and Sensor Data.
State building” is contingent on building indices that group the points-of-interest
(POI) data.
Earth sciences and geo-spatial data: Spatial clustering on climatology data
has been used to characterize regions with varying weather patterns [95]. In another effort [110], large datasets from astronomical studies are analyzed to clusters
of galaxies. Shape-based clustering has also been applied to seismic data to understand earthquake patterns [5]. [47] serves as a good survey of related techniques.
Epidemiology and disease clusters: Another application of shape-based clustering comes from the health care domain, wherein early detection of disease outburst
can be achieved by observing the spatial distribution of the disease instances [72, 69].
Furthermore, understanding disease clusters can help analyze spread of an out-
6
break [71].
Global Information Systems (GIS) data: Ecoregions – areas of land or water
characterized by presence of certain types of flora or fauna, soil type, animal communities, etc. – can be captured [49] using shape-based clustering. The detection of
such regions impacts conservation activities for wildlife and forests. Segmentation
of sensor fields is crucial for understanding placement of sensors and master nodes.
Spatial clustering methods have been applied for segmenting sensor networks [128]
and for grouping sensor networks considering the energy efficiency criteria [42]. Clustering algorithms have been used on geo-spatial satellite images and remote sensing
digital images to identify regions with irregular shapes [101], such as bridges, rivers
and roads.
Figure 1.1(c)3 shows the remote sensing image of the California forest fire.
Similarly, Figure 1.1(b)4 shows a satellite image of the cloud formation during Hurricane Katrina. Image segmentation methods based on shaped-based clustering can
help identify regions of interest in these images. Similar applications appear within
biological image analysis, such as chromosome separation. Figure 1.1(d) 5 shows an
image used for chromosome separation.
1.2.2
Problem Formulation and Contribution
Traditional clustering algorithms have focused on the following objectives: 1)
improving the clustering quality, 2) improving efficiency, and 3) designing algorithms
that can scale to larger datasets. The last consideration is gaining prominence as
the sizes of the datasets are growing at a steady pace. Shape-based clustering becomes challenging for large datasets since standard distance measures and parametric models are unable to capture arbitrary shaped clusters. Although density-based
algorithms have been proposed to overcome this limitation, they suffer from a high
computational complexity and sensitivity to parameters. Similarly, spectral clustering algorithms suffer from scalability issues.
Existing approaches to clustering tackle scalability issues through the following
3
Image taken from http://www.geology.com
Image taken from http://www.usgs.gov/ngpo/
5
Image taken from http://www.riken.go.jp/asi/images/kaleidoscope/chromosome.jpg
4
7
methods:
1. Distributed clustering algorithms: This approach to clustering large scale
datasets, scales up the resources (CPU and memory) proportionately. Distributed and parallel versions of existing clustering algorithms can deal with
large datasets. For instance, [61] discusses a distributed density based clustering algorithm and [92] describes a parallel version of BIRCH. Recently,
cluster computing paradigms such as Map-Reduce have also been employed
for scalability purposes [21].
2. Sampling based methods: rely on applying clustering algorithms on a
randomly selected sample of the data [119]. The underlying assumption is that
the results on the sample would apply to the entire dataset. CLARANS [88]
CURE [45] and DBRS [116] are examples of this approach. Factors such as
the size of the sample would affect the quality of the clustering. Also, these
methods scale well but on the down side they rely on uniform size and density
of the clusters.
3. Data summarization methods: Somewhat related to the sampling based
methods, this class of algorithms aims at identifying representatives within
the large dataset. Standard clustering algorithms can be applied over this
summary dataset. Final clustering is obtained by mapping the representatives
to the original set of points. This approach is taken by CSM [75].
Another approach is to “intelligently” reduce the dataset size. With a significantly smaller dataset, even computationally expensive algorithms can be applied.
Reducing the dataset size in a principled manner to achieve scalability is the driving theme for the algorithms proposed in this thesis. In this thesis, we propose two
simple, yet highly scalable algorithm for mining clusters of arbitrary shapes, sizes
and densities.
We call our first algorithm SPARCL (which is an anagram of the bold letters in ShAPe-based CLusteRing). In order to achieve this we exploit the linear
(in the number of objects) runtime of Kmeans based algorithms while avoiding its
8
drawbacks. Kmeans based algorithms assign all points to the nearest cluster center; thus the center represents a set of objects that collectively approximates the
shape of a d dimensional hypersphere. When the number of centers are few, each
such hypersphere covers a larger region, thus leading to incorrect partitioning of a
dataset with arbitrary shapes. Increasing the number of centers reduces the region
covered by each center. SPARCL exploits this observation by first using a smart
strategy for sampling objects from the entire dataset. These objects are used as initial seeds of the Kmeans algorithm. On termination, Kmeans yields a set of centers.
In the second step, a similarity metric for each pair of centers is computed. The
similarity graph representing pairwise similarities between the centers is partitioned
to generate the desired final number of clusters.
The second algorithm proposed in this thesis is inspired from the concept of
skeletonization from the image processing literature. A skeletonized dataset is much
smaller as compared to the original dataset and has much less noise. The reduction
in the amount of noise makes the data cleaner resulting in efficient identification of
the clusters. The reduction in the dataset size, on the other hand, contributes to
the scalability of the clustering algorithm. In order to achieve the same effect as
skeletonization we define two operations on the data – globbing and displacement.
These two operations are performed on the dataset in an iterative fashion. The
stopping criteria for the iterative process is based on a Minimum Description Length
(MDL) principle formulation. On termination, a skeletonized dataset is obtained.
In a second step, clusters from the reduced dataset are obtained, either by applying
a hierarchical or a spectral clustering algorithm.
To summarize we made the following key contributions in this work:
1. We propose a new, highly scalable algorithm, SPARCL, for arbitrary shaped
clusters, that combines partitional and hierarchical clustering in the two phases
of its operation. The overall complexity of the algorithm is linear in the number
of objects in the dataset.
2. SPARCL takes only two parameters – number of initial centers and the number
of final clusters expected from the dataset. Note that the number of final
clusters to find is typically a hyper-parameter of most clustering algorithms.
9
3. Within the second phase of SPARCL we define a new function that captures
similarity between a pair of cluster centers. This function encapsulates the
distance between the clusters as well as the density of the pair of clusters.
4. The second backbone detection based algorithm, applies two simple operations – globbing and displacement – on the dataset to identify the skeleton
(backbone) of the clusters. On repeated application of these operations, the
cluster backbone emerges. Hierarchical clustering on the backbone produces
the final set of clusters.
5. We perform a variety of experiments on both real and synthetic shape clustering datasets to show the strengths and weaknesses of our approaches. We
show that our methods are an order of magnitude faster than the best current
approaches.
1.3
Thesis Outline
Chapter 2 provides a comprehensive introduction to clustering algorithms,
with specific emphasis on shape-based clustering algorithms. Certain key shapedbased clustering algorithms from the literature are discussed. Chapter 3 focuses on
the SPARCL algorithm. Chapter 3 also provides a thorough experimental comparison with related algorithms. Chapter 4 introduces the second algorithm for identifying arbitrary shaped clusters. Since SPARCL performs better than the state-ofthe-art algorithms, as a result the backbone based algorithm in Chapter 4 focuses
on comparison with SPARCL. Finally, Chapter 5 discusses the future directions.
Future efforts involve extending SPARCL to identify clusters in subspaces. Some
other directions include using the seed selection procedure outlined in Chapter 3 to
index shapes. Using concepts from graph sparsification literature to obtain a sparse
data is another interesting line of work to improve scalability. The concept of tree
spanners is one such idea.
CHAPTER 2
Background and Related Work
This chapter covers fundamentals of clustering followed by an overview of various
clustering algorithms. A few shape-based clustering algorithms (such as DBSCAN
and CHAMELEON) are discussed in further detail since we compare SPARCL with
them in Chapter 3.
2.1
2.1.1
Clustering Preliminaries
Data Types
The objects in the dataset are assumed to be in a d-dimensional feature space.
The type of data associated with each feature determines the overall type of the
object. Depending on the application, each feature of an object can have a different
data type associated with it. The most common data types include numeric, binary,
categorical (also known as nominal ), ordinal or a combination of them. Numeric
features have real values. Binary features capture the presence or absence of the
feature for an object. Categorical data is a generalization of binary data to more
than two choices. Ordinal data is characterized by the presence of order information
between them. For instance, the medal tally of countries taking part at Olympics,
wherein gold, silver and bronze have an order associated with them. Most clustering
algorithms are catered towards numeric data. while some others can handle categorical data [38, 46]. A few can cluster mixed data, i.e., some categorical features
along with numerical features [20].
2.1.2
Distance Measures
The main operation in clustering is to group similar objects together and to
keep dissimilar objects far apart. The similarity is defined in terms of some distance
metric. The distance measure is chosen based on the data types associated with the
features of an object. A variety of distance measures have been proposed in the
literature, which include:
10
11
Minkowiski distance: of order p (p-norm distance), is given by
dist(x, y) =
d
X
| xi − yi |
i=1
p 1/p
(2.1)
where x, y ∈ Rd and xi represents the value at the ith dimension. Minkowiski
distance is applicable for d-dimensional Euclidean spaces. Manhattan distance and
Euclidean distance are special cases of Minkowiski distance with p = 1 and p = 2,
respectively.
Object y
1
0
1
a
b
0
c
d
Object x
Figure 2.1: Contingency Table for Jaccard Co-efficient
Jaccard Coefficient: The distance between two binary valued objects can be
calculated with the Jaccard Coefficient. Given the contingency table as shown in
Figure 2.1, the Jaccard coefficient is given by
sim(x, y) =
a
a+b+c
(2.2)
where a and d indicate the number of dimensions in which the two objects have
the same binary value of 1 and 0, respectively. Similarly, c and b count the number
of dimension in which the two objects have different binary values. The Jaccard
coefficient is an asymmetric measure. A symmetric distance measure for binary
data computes the ratio of number of dissimilar features to the total number of
features, given by
sim(x, y) =
b+c
a+b+c+d
(2.3)
12
Cosine Measure: In order to compute the cosine distance, the set of features for
each object is treated as a vector. The distance between two objects is the cosine
of the angle between the corresponding vectors. This measure is frequently used for
text documents, due to its scale and length invariant properties.
The choice of the distance/similarity measure is also dependent on the application and the properties of the data. For instance, Discrete Wavelet Transform [63],
Discrete Fourier Transform [79] and Dynamic Time Warping [66] are favorably
used for time-series data; edit distance and its variations for sequence data such
as protein/gene sequence; Pearson Correlation [98] for collaborative filtering; and
Spearman correlation [107] for ordinal data.
2.2
Dominant Clustering Paradigms
In the following section, we outline some properties based on which the clus-
tering algorithms can be distinguished. Some of these properties pertain to the
output of the clustering algorithms, some others to the type of data accepted by the
algorithm and the rest to the parameters associated with the algorithms.
2.2.1
Differentiating Properties
Since the field of cluster analysis has been in existence for a long time, many
clustering algorithms have been proposed. Although many of these algorithms might
seem similar at the outset, there is a set of properties that can help differentiate
between them. Observing the algorithms with respect to these properties, brings
out the differences between them. The properties have been organized into related
groups.
Performance: Properties related to the efficiency and scalability of the algorithm.
• Time and Space complexity: The time and space complexities are important from the point of scalability to larger datasets. This also includes the
fact whether the algorithm needs the entire pair-wise similarity (or distance)
13
matrix to be computed. For large datasets, computing the entire pair-wise
similarity matrix is prohibitive, both in terms of space and time.
• High-dimensionality: Can the algorithm scale to higher dimensions?
Membership: Properties related to the membership/representative information
resulting from the algorithm.
• Representatives: Does the algorithm produce a set of representatives for
the identified clusters?
• Hard versus soft: Does the algorithm assign each object to a single fixed
cluster (hard clustering) or does it result in a probability distribution over
cluster membership (soft clustering)?
• Outlier Detection: Does the algorithm distinguish between outliers and
cluster members, or are outliers assigned to one of the identified clusters?
Robustness: Properties capturing sensitivity to external effects.
• Data order dependency: Does the output or performance of the algorithm
depend on the order in which the points are processed?
• Parameters and their effect: Algorithms with smaller number of parameters are favored. Moreover, it is important to understand the effect of changes
in the parameter values on the final clustering. Sensitivity of the clustering
results to changes in parameter values reflects the lack of robustness of the
algorithm. A robust algorithm is definitely preferred.
Cluster type: Properties that capture the type of clusters identified by the algorithm.
• Shape-based clusters: Is the algorithm able to identify clusters with arbitrary shapes and diverse densities?
• Subspace clusters: Can the algorithm identify clusters that lie in a subset
of the d dimensions, called a subspace. Each cluster can belong in a different
subspace.
14
Input Parameters: Properties related to inputs provided to the algorithm.
• Data type: Defines the data types (from Section 2.1.1) that can be handled
by the algorithm.
• Distance measure: The distance measures (from Section 2.1.2) that can be
used by the algorithm.
• Prior knowledge: Does the algorithm depend on assumptions regarding the
data. This naturally restricts the applicability of the algorithm to a wide range
of datasets.
2.2.2
Categorization
Due to the large number of potential application domains, many flavors of
clustering algorithms have been proposed [59, 84]. Categorizing them helps in understanding their differences. Although Section 2.2.1 outlined some of the differentiating properties, the mode of operation is the most common basis of categorization.
Figure 2.2 provides a taxonomy of clustering algorithms based on their mode of
operation. Broadly, they can be categorized as variance-based, hierarchical, partitional, spectral, probabilistic/fuzzy and density-based. However, the common task
among all algorithms is that they compute the similarities (distances) among the
data points to solve the clustering problem. The definition of similarity or distance
varies based on the application domain. For instance, if the data instance is modeled
as a point in d-dimensional linear subspace, Euclidean distance generally works well.
However, in applications like image segmentation or spatial data mining, Euclidean
distance based measure does not generate the desired clustering solution. Clusters in
these applications generally form a dense set of points that can represent (physical)
objects of arbitrary shapes. The Euclidean distance measure fails to isolate those
objects since it favors compact and spherical shaped clusters. Below we review each
of the major clustering paradigms (as illustrated in Figure 2.2).
2.2.2.1
Partitional Clustering
The partitioning based methods aim to divide the set of objects D into k
disjoint sets. An optimal clustering is obtained when the division of objects results
15
Agglomerative
Hierarchical
Divisive
k−Means
Partitional
k−Medoids
Probabilistic
Cluster Analysis
Algorithms
Expectation
Maximization
Graph−theoretic
Connectivity−based
Density−based
Density−function
based
Grid−based
Spectral
Evolution + Neural−net
based
SOM
Figure 2.2: Taxonomy of Clustering Algorithms
in k sets such the following two conditions are satisfied: (1) points in a set are
“close” to other points in the same set, (2) points belonging to two different sets are
as “far apart” as possible. To obtain the optimal clustering one has to enumerate all
possible partitions. Since the number of partitions are exponential in the number
of objects, this approach is naturally unfeasible.
This leads to (non-optimal) algorithms that incrementally obtain a better partitioning based on certain heuristics. Such algorithms are known as iterative relocation methods, based on their mode of operation. The algorithms start with
16
a random partitioning
6
of the objects. In each subsequent iteration the points can
be moved to a different cluster, as long as the quality of the clustering is improved.
The procedure concludes when moving the points does not lead to any further improvement in the quality of the clustering. Partitional algorithms broadly fall under
two sub-categories:
k-means: In this strategy, each cluster is represented by a mean point. The mean
point is the arithmetic mean of all the points belonging to a cluster, along each
dimension. During each iteration, objects are assigned to the mean point closest
to them. This could change the objects assigned to a cluster, which in turn could
change the mean point. This process continues until one of the following conditions
is satisfied: (1) no object moves to a different cluster, or (2) the change in the mean
points for each cluster is below a pre-determined threshold. The clustering quality
metric for k-Means is the Sum of Square Error (SSE). The SSE also serves as
the optimization criteria for the k-Means procedure. Given a clustering C with
clusters C1 , C2 , ..., Ck , the Sum of Square Error is given by
SSE(C) =
k X
X
|| xi − cj || 2
(2.4)
j=1 xi ∈Cj
where the objects are represented by xi , and cj is the mean point for cluster Cj .
It can be shown that for the above SSE, the k-means algorithm converges monotonically to a local minima. We outline the k-means algorithm in Figure 2.3. This
version of k-means is popularly known as the Lloyd’s algorithm [77]. The random
initialization is attributed to Forgy [36]. The described algorithm has a time complexity that is linear in the number of points and the number of clusters. The
complexity can be denoted by O(nke), where e is the number of times lines 4–9 are
executed.
k-medoids: The k-medoids is a variation of the k-means strategy. Here, each
cluster is represented by the medoid of the cluster. A medoid is the object that is
closest to the center of the cluster. Medoids are less affected by outlier points, as
6
Some other initializations have also been proposed in the literature which are discussed later.
17
k-means(D, k):
1. Cinit = pick random init center(D, k)
2. M = assign obj to center(D, Cinit )
3. repeat
4. Cnew = compute centers(D, M)
5. Mnew = assign obj to center(D, Cnew )
6. change = compute change(M, Mnew )
7. M = Mnew
8. until change == true
Figure 2.3: The k-means Algorithm
a result the medoids based approach is more robust. At the same time, computing
medoids is computationally more expensive as compared to computing means.
2.2.2.2
Hierarchical Clustering
Hierarchical clustering, as the name suggests, creates a hierarchy of clusters.
The hierarchical arrangement of the clusters results in a tree-like structure called a
dendrogram. Broadly, two disparate approaches are proposed in the literature for
obtaining hierarchical clusters. Agglomerative hierarchical clustering starts
out with each point being in a separate cluster. During each subsequent step, the
“closest” clusters are merged to form a new cluster at a higher level in the hierarchy.
This process continues till the desired number of clusters are obtained. Divisive
hierarchical clustering takes a top-down approach. It starts with a single cluster
consisting of all the objects. At each step, a cluster is broken into two sub-clusters,
until a stopping condition is satisfied. Examples of stopping condition includes: (1)
reaching the desired number of clusters, or (2) the minimum distance between a
pair of clusters being greater than a predetermined threshold.
For agglomerative
clustering the following distance measures are commonly used:
1. Single-link [106]: The distance between two clusters Ci and Cj is given by the
minimum distance between two points, one of which is in Ci and the other in
Cj .
SL(Ci , Cj ) = min{dist(x, y) | x ∈ Ci , y ∈ Cj }
(2.5)
18
2. Complete-link, also known as the farthest neighbor, is given by the expression
CL(Ci , Cj ) = max{dist(x, y) | x ∈ Ci , y ∈ Cj }
(2.6)
3. Average-link [111], also known as the minimum variance method, determines
the distance between two clusters by the expression
AL(Ci , Cj ) =
P
x∈Ci ,y∈Cj
dist(x, y)
| Ci | × | Cj |
(2.7)
Hierarchical clustering, unlike partitional clustering, does not change the cluster
membership of an object. Smaller clusters can be merged to form bigger clusters,
but otherwise objects cannot drastically change membership. This is an inherent
drawback of the hierarchical mode of the clustering.
Some clustering algorithms combine hierarchical clustering with other clustering algorithms. BIRCH [126], builds a tree-like summary structure (called Clustering
Feature tree) corresponding to the hierarchical arrangement. Conceptually, the CF
tree is similar to a B+-tree. Each node of the CF tree contains the summary statistics for the cluster corresponding to the tree node. In the second step, BIRCH
employs any clustering algorithms to cluster the leaf nodes of the CF tree. Another
algorithm, CURE [45], combines the centroid-based approach with hierarchical clustering. Instead of assigning a single centroid to a cluster, a large number of centroids
are associated with a cluster. The distance between two clusters is the single-link
distance between the centroids of the clusters. Additionally, the centroids associated
with a cluster are pulled in towards the center of the cluster by a fixed fraction of the
distance. This enables CURE to capture clusters that are non-spherical in shape.
CHAMELEON is another popular clustering algorithm. CHAMELEON employs a
combination of graph-partitioning and hierarchical clustering to obtain the final set
of clusters. It can capture clusters with arbitrary shapes and sizes. CHAMELEON
is discussed in detail in Section 2.3.2.
19
2.2.2.3
Probabilistic/fuzzy Clustering
Under fuzzy/probabilistic clustering each object x is assigned a probability of
belonging to a cluster Ci . The concept of probabilistic membership is commonly
known as soft clustering. The most popular fuzzy clustering algorithm is the Fuzzy
C-Means [10] which is a variation of the regular k-means. In Fuzzy C-Means, the
following weighted squared error is minimized
J=
n X
k
X
i=1
Pn
uij xi
uij || xi − cj || cj = Pi=1
n
i=1 uij
j=1
2
(2.8)
where uij is the fraction denoting the likelihood of object xi belonging to cluster Cj
with center cj . It can be shown that with this objective function, a local optima
can be reached following the k-means style algorithm.
Expectation Maximization (EM) [28] algorithm is a popular algorithm for probabilistic clustering. For a mixture model wherein each cluster is generated from
a distribution, the EM algorithm determines the parameter values for the distributions. Expectation Maximization is a Maximum Likelihood Estimation (MLE)
method for the mixture parameters. Intuitively, maximum likelihood estimate selects the parameters values that maximize the likelihood of the observed data. If
the parameters are indicated by the variable α = {α1 , α2 , . . . , αk }, the EM selects
the value of α that maximizes the probability P r(D | α). Like k-means, EM is an
iterative algorithm. Each iteration is composed of two steps:
• E-step: In this step the algorithm computes a lower bound for the expected
value of the likelihood function, under the current estimates of the parameters.
• M-step: In the M-step, the algorithm computes the new estimate for the
parameters which maximizes the expected value of the likelihood function
computed in the E-step.
2.2.2.4
Graph-theoretic Clustering
Vast amount of work has been done within the graph-theory and network
analysis community on clustering algorithms. Usually, the approach taken involves
20
concepts related to influence propagation, graph cut algorithms or community detection methods. In [37], the authors use the concept of affinity propagation between
data points (objects). In this iterative algorithm, messages reflecting the affinity
of a node towards another are passed between nodes. The result of this process
is a set of “exemplars” that correspond to the cluster representatives. Each point
is associated with the closest “exemplar”. Other algorithms that are grounded in
concepts from network flow include [33, 56]. With the popularity of social networks
there has been a renewed interest in graph-based clustering methods. In an earlier
work [48], the authors propose the concept of separating operators, when applied
iteratively to the nodes, brings out the clusters within a graph. The authors define
a separating operator based on the circular escape probability between nodes in a
graph.
2.2.2.5
Grid-based Clustering
The grid based clustering methods operate by partitioning the d-dimensional
space along each dimension. This results in a grid-like structure over the input space.
STING (STatistical INformation Grid) [115] is an example of grid-based clustering.
For each cell resulting from the grid, STING captures statistical information (e.g.
standard deviation, mean, etc.) from the objects within that cell. This forms the
first level of cells. Like hierarchical clustering, cells belonging to the first levels are
combined to form larger cells at the next level. The statistical attributes of cells
at higher resolution can be computed from the cells in the immediate lower level.
As such, STING provides a multi-resolution clustering. Another grid-based algorithmWaveCluster [104], utilizes concepts from signal processing. After generating
the grids, WaveCluster applies discrete Wavelet transform to the objects within a
cell. The wavelet transform identifies boundaries of the clusters as high frequency
regions. Neighboring cells are combined using connected components.
2.2.2.6
Evolution and Neural-net based Clustering
Many clustering algorithms have been proposed from the neural networks and
genetic algorithms communities. A Self Organizing Map (SOM), also known as a
Kohonen map, is a type of artificial neural network that uses a vector quantization
21
technique to map objects in high dimensional data space to a lower dimensional
space. This mapping leads to grouping of objects in the lower dimensional space.
SOMs were initially designed as a data visualization technique. From the evolutionary computing side, genetic algorithms have also been used for clustering [82], to
navigate the feature space in search of appropriate cluster centers.
Due to the large body of work related to clustering, a complete coverage of
the algorithms is beyond the scope of any single document. For instance, clustering
algorithms that draw inspiration from natural and physical phenomenon – colonies
of ants [11], flocks of birds [25], force of gravity [58] and magnetic fields [12] – have
not been discussed.
The algorithms discussed above are specifically for identifying groups of related
objects. Although not stated explicitly, these algorithms assume that the objects in
a cluster span across all the dimensions. Such algorithms are known as full space
clustering algorithms. Certain clustering algorithms, called subspace clustering
algorithms, identify clusters that lie in a space spanned by a subset of the dimensions or some linear/non-linear combination of the dimensions. Given a dataset of
objects, these algorithms are able to capture the subspaces spanned by the objects
in a cluster [3, 94].
Additional data in the form of constraints can be provided to a clustering
algorithm. Common forms of constraints include instance level must-link constraints
and instance level cannot-link constraints. The must-link constraint between a pair
of objects enforces the points to belong to the same cluster. On the other hand,
a cannot-link constraint disallows a pair of objects from being grouped together in
the same cluster. Algorithms that incorporate constraints are commonly known as
constraint based clustering algorithms [26].
Certain recent classes of algorithms treat the objects in d-dimensional space
as a 2-dimensional n × d matrix. Linear algebra based factorization methods, such
as Non-negative Matrix Factorization [73], have been shown to be related to conventional methods such as k-means and spectral clustering. Another branch within
clustering, termed co-clustering [29], aims at grouping features in addition to the
objects. For every object cluster, a group of features is associated, such that a high
22
correlation exists between the object-feature pairs.
2.3
Review of Shape-based Clustering Methods
A comprehensive survey of arbitrary shape clustering with a focus towards
spatial clustering is provided in [84]. Here we review some of the pioneering methods.
2.3.1
Density-based Clustering
D
D
Noise point
C
C
B
B
A
A
Core point
Noise point
eps
(a)
(b)
Figure 2.4: DBScan – Density reachability, core points and noise points.
minPts = 2
DBSCAN [34] was one of the earliest algorithms that addressed arbitrary shape
clustering. It defines two parameters – eps which is the radius of the neighborhood
of a point, and MinPts which is the minimum threshold for the number of points
within eps radius of a point. A point is labeled as a core point if the number of points
within its eps neighborhood is at least MinPts. Based on the notion of density-based
reachability, a cluster can be defined as the maximal set of reachable core points, i.e.,
such that each core point is within the eps neighborhood of at least one other core
point in the cluster. Other (border) points that are with the neighborhood of core
points are also added to the same cluster (ties are broken arbitrarily or in the order
of visitation). Points that are not core and not reachable from a core are labeled
as noise. Figure 2.4 shows the three clusters obtained with minPts set to 2. Points
A through D are core points and D is density reachable from A. Two noise points
23
are shown in Figure 2.4(b). The main advantages of DBSCAN are that it does not
require the number of desired clusters as an input, and it explicitly identifies outliers.
On the flip side, DBSCAN can be quite sensitive to the values of eps and MinPts,
and choosing correct values for these parameters is not that easy. DBSCAN is also
an expensive method, since in general it needs to compute the eps neighborhood
for each point, which takes O(n2 ) time, especially with increasing dimensions; this
time can be brought down to O(n log n) in lower dimensional spaces, via the use of
spatial index structures like R∗ -trees.
DENCLUE [52, 54] is a density based clustering algorithm based on kernel
density estimation. DENCLUE models the impact of a data point within its neighborhood as an influence function. The influence function is defined in terms of
the distance between the two points. The density function at a point in the data
space is expressed in terms of the influence functions acting on that point. Clusters are determined by identifying density attractors which are local maxima of the
density function. The density attractors are identified by performing a gradient
ascent type algorithm over the space of influence functions. Both center-defined
and arbitrary-shaped clusters can be identified by finding the set of points that are
density attracted by a density attractor. DENCLUE shares some of the same limitations of DBSCAN, namely, sensitivity to parameter values, and its complexity is
O(n log m + m2 ), where n is the number of points, and m is the number of populated cells. In the worst case m = O(n), and thus its complexity is also O(n2 ). The
recent DENCLUE2.0 [53] method practically speeds up the time by adjusting the
step size in the hill climbing approach. An extension [31] of DENCLUE, proposes a
grid approximation to deal with large datasets.
2.3.2
Hierarchical Clustering
The arbitrary shape clustering problem has also been modeled as a hierarchi-
cal clustering task. For example, Kaufman and Rousseeuw [65] proposed one of the
earliest agglomerative method that can handle arbitrary shape clusters, which they
termed as elongated clusters. They compute the similarity between two clusters A
and B as the smallest distance between a pair of objects from A and B respectively.
24
This method is computationally very expensive due to the expensive similarity computations, with a complexity of O(n2 log n). Moreover, presence of outlier points
between the boundary region of two distinct clusters can cause wrong merging decisions. In a recent work [68], the authors propose a hierarchical clustering algorithm
based on an approximate nearest neighbor search – Locality-Sensitive Hashing [4].
This approach considerably improves the time complexity of the algorithm.
CURE [45] is another hierarchical agglomerative clustering algorithm that handles shape-based clusters. It follows the nearest neighbor distance to measure the
similarity between two clusters as in [65], but reduces the computational cost significantly. The reduction is achieved by taking a set of representative points from each
cluster and engaging only these points in similarity computations. To ensure that
the representative points are not outlier points, the representatives are pulled in, by a
predetermined factor, towards the mean of the cluster. CURE is still expensive with
its quadratic complexity, and more importantly, the quality of clustering depends
enormously on the sampling quality. In [64], the authors show several examples
where CURE failed to obtain the desired shape-based clusters. CHAMELEON [64]
Figure 2.5: CHAMELEON Clustering Steps. Figure from [64]
also formulates the shape-based clusters as a hierarchical clustering problem over
a graph partitioning algorithm. A m nearest neighbor graph is generated for the
input dataset, for a given number of neighbors m. This graph is partitioned into
a predefined number of sub-graphs (also referred as sub-clusters). The partitioned
sub-graphs are then merged to obtain the desired number of final k clusters. This
process is illustrated in Figure 2.5. CHAMELEON introduces two measures – rel-
25
ative inter-connectivity (RI) and relative closeness (RC) – that determine if a pair
of clusters can be merged. Relative inter-connectivity is defined as ratio of the total
edge cut between the two sub-clusters and the mean internal connectivity of the
sub-clusters. It is given by the expression
RI =
EC(Ci , Cj )
+ EC(Cj ))
1
(EC(Ci )
2
(2.9)
where EC(Ci , Cj ) is the sum of the edges in the m-nearest neighbor graph that
connect cluster Ci and Cj , EC(Ci ) is the minimum sum of the cut edges if cluster Ci
is bisected. The internal connectivity is defined as the weight of the cut that divides
(a)
Figure 2.6: CHAMELEON
from [64].
(b)
–
Relative
Interconnectivity.
Figure
a sub-cluster into equal parts. The relative inter-connectivity measure ensures that
sub-clusters having a small bridge connecting them are not merged together. The RI
measure can be explained using Figure 2.6. Although both Figures 2.6(a) and 2.6(b)
have almost the same edge cut, the mean internal connectivity is very different.
The two circular clusters in Figure 2.6(b) have a much higher internal connectivity
resulting is a smaller value for RI.
Relative closeness is the ratio of the absolute closeness to the internal closeness of
the two sub-clusters, where absolute closeness is the mean edge cut between the two
clusters, and the internal closeness of a cluster is the average edge cut that splits it
into two equal parts. It is given by the expression
RC =
S̄EC (Ci , Cj )
mj
mi
S̄ (Ci ) + mi +m
S̄EC (Cj )
mi +mj EC
j
(2.10)
where mi and mj are the sizes of clusters Ci and Cj respectively. S̄EC (Ci , Cj ) is the
26
average weight of the edges between clusters Ci and Cj and S̄EC (Ci ) is the average
weight of the edges if cluster Ci was bisected. Relative closeness ensures that the
two merged sub-clusters have the same density. Moreover, this measure ensures
that the distance between the two sub-clusters is comparable with their internal
densities. Sub-clusters having high relative closeness and relative inter-connectivity
are merged. CHAMELEON is robust to the presence of outliers, partly due to the
m-nearest neighbor graph which eliminates these noise points. This very advantage,
turns into an overhead when the dataset size becomes considerably large, since computing the nearest neighbor graph can take O(n2 ) time as the dimensions increase.
Figure 2.7 helps understand the RC measure. The S̄EC (Ci , Cj ) measure for the
clusters in Figure 2.7(a) is small as compared to the denominator in Equation 2.10.
This results in a small value for RC for these clusters. On the other hand, even
though the S̄EC (Ci , Cj ) value for the clusters in Figure 2.7(b) might be small, the
denominator is also small due to the within cluster sparsity. The net effect is a high
value for RC, indicating a possible merger of the two clusters.
(a)
(b)
Figure 2.7: CHAMELEON – Relative Closeness. Figure from [64].
2.3.3
Spectral Clustering
Proposed in the pattern recognition community, the spectral clustering meth-
ods are capable of handling arbitrary shaped clusters. The data points are represented as a weighted undirected graph, where the weights denote the similarities
between the nodes (data points). Let W be the symmetric weight matrix. The degree of the nodes in the graph is captured in the diagonal matrix D as d1 , d2 , . . . , dn .
The Normalized Laplacian matrix L is given by L = I − D−1 W .
worst case: O(n2 )
O(n)
O(n)
worst case: O(nlogn)
O(cd )
O(n)
SPARCL (2008)
O(n)
Somewhat
Somewhat
Yes
No
Somewhat
Yes
Yes
Yes
Yes
Yes
Yes
No
No
No
No
No
No
T : radius of
α: shrinkage factor
points within eps
minPts: minimum no. of
eps: radius
L: Entries in a leaf
leaf clusters,
s: random sample size
K: # of pseudo-centers
algorithm
Depends on exact
parameters for RI and RC
p, M IN SIZE, k,
not required
c, no. of final clusters
ξ: noise threshold
σ: density parameter
c: # of representatives
Table 2.1: Summary of spatial (shape-based) Clustering Algorithms
worst case:O(n3 )
O(n2 )
s: # of small
clusters generated
O(pn)
p: # of nearest neighbors
O(ns + nlogn + s2 logs)
each dimension
c: # cells in
O(n)
worst case: O(nlogn)
Somewhat
No
No
Yes
Parameters
p: # of clusters
Yes
Yes
Somewhat
Dependent
Input Order
schemes reduce complexity
Yes
Not very well
Somewhat
Clusters
Irregular Shaped
p: # of partitions
O(n2 logn)
Handles high
dimensionality
Comparison Metrics
Sampling+partitioning
O(n)
O(n)
factor
spatial index: O(nlogn)
O(n)
incremental
O(nB), B: branching
Space
Requirement
Time
Efficiency
Spectral (Shi-Malik, 2000)
CHAMELEON (1999)
WaveCluster (1998)
DENCLUE (1998)
CURE (1998)
DBSCAN (1996)
BIRCH (1996)
Algorithms
Clustering
Part of clusters
Part of clusters
to clusters
Assigns noise points
points
Identifies noise
at 2 stages
Identifies noise points
points.
Identifies noise
points
Identifies noise
Handling Noise
27
28
The Laplacian matrix possesses some nice linear algebra properties, such as,
being positive semi-definite. In [105] the authors formulate the arbitrary shape
clustering problem as a normalized min-cut problem. The normalized cut for a
graph with partitions A1 , . . . , Ak is given by the expression
N cut(A1 , · · · , Ak ) =
k
X
cut(Ai , Āi )
i=1
where cut(A, B) =
P
i∈A,j∈B
wij and vol(A) =
vol(Ai )
P
i∈A,j∈A
(2.11)
wij . The minimization of
the normalized cut criterion tends to result in clusters that are “balanced”. While
the simple cut() criterion has a polynomial time solution, the same cannot be said
for the normalized cut problem [114]. A relaxed version of the problem is solved
using spectral graph theory. The solution to the relaxed version is an approximation
that is obtained by computing the eigenvectors of the graph Laplacian matrix.
The basic idea is to partition the similarity graph based on the eigenvector
corresponding to the second smallest eigenvalue (the smallest eigenvalue is always
0 with eigenvector 1) of the Laplacian matrix. If the desired number of clusters
are not obtained the subgraphs are further partitioned using the lower eigenvectors
as approximations for the second eigenvector of the subgraphs. The intuitive reason of its success is its alternate similarity measure which is shape-insensitive. [83]
shows that the similarity between two data points in the normalized-cut framework
is equivalent to their connectedness with respect to the random walks in the graph,
where the transition probability between nodes is inversely proportional to the distance between the pair of points. Although based on strong theoretical foundation,
this method, unfortunately, is not scalable, due to its high computational time and
space complexity. It requires O(n3 ) time to solve the Eigensystem of the symmetric Laplacian matrix, and storing the matrix also requires at least Ω(n2 ) memory.
There are some variations of this general approach [124], but all suffer from the
poor scalability problem. von Luxburg [80] provides a good ground up tutorial on
spectral clustering. Table 2.1 provides a summarized comparison of shape-based
clustering algorithms that have been proposed in the literature. They are arranged
in chronological order.
29
2.3.4
SPARCL – Brief Overview
Our proposed method SPARCL [18] is based on the well known family of
Kmeans based algorithms, which are widely popular for their simplicity and efficiency [122]. Kmeans based algorithms operate in an iterative fashion. From an
initial set of k selected objects, the algorithm iteratively refines the set of representatives with the objective of minimizing the mean squared distance (also known as
distortion) from each object to its nearest representative. Kmeans based methods
are characterized by O(n d k e) time complexity, where e represents the number of
iterations the algorithm runs before convergence. They are related to Voronoi tessellation, which leads to convex polytopes in metric spaces [90]. As a consequence,
Kmeans based algorithms are unable to partition spaces with non-spherical clusters
or in general arbitrary shapes. However, in this thesis we show that one can use
Kmeans type algorithms to obtain a set of seed representatives, which in turn can
be used to obtain the final arbitrary shaped clusters. In this way, SPARCL retains
the linear time complexity in terms of the data points, and is surprisingly effective
as well, as we discuss next. Note that SPARCL focuses on full-space shape-based
clusters.
2.3.5
Backbone based Clustering – An Overview
The backbone based clustering algorithm is inspired by the concept of skele-
tonization from the image processing literature. We assume a hypothetical generative process for obtaining clusters with arbitrary shapes given the backbone. Our
idea is based on outlining this generative process in reverse. The resulting skeletonized dataset is much smaller as compared to the original dataset and has much
less noise. The reduction in the amount of noise makes the data cleaner leading to
efficient identification of the clusters. The reduction in the dataset size, on the other
hand, contributes to the scalability of the clustering algorithm. In order to achieve
the same effect as skeletonization we define two operations on the data – globbing
and displacement. These two operations are performed on the dataset in an iterative fashion. The stopping criteria for the iterative process is based on a Minimum
Description Length (MDL) principle formulation. On termination, a skeletonized
30
dataset is obtained. The entire process takes a single parameter – the number of
nearest neighbors. In the second step of the algorithm, clusters from the reduced
dataset are obtained, either by applying a hierarchical or a spectral clustering algorithm. We are currently exploring methods by which the clusters can be detected
without specifying the desired number of clusters as a parameter to the hierarchical
or spectral clustering algorithm.
CHAPTER 3
SPARCL: Efficient Shape-based Clustering
In this chapter we focus on a scalable algorithm for obtaining clusters with arbitrary
shapes. In order to capture arbitrary shapes, we want to divide such shapes into convex pieces. This approach is motivated by the concept of convex decomposition [100]
from computational geometry.
Convex Decomposition: Due to the simplicity of dealing with convex shapes,
the problem of decomposing non-convex shapes into a set of convex shapes has been
of great interest in the area of computational geometry. A convex decomposition
is a partition, if the polyhedron is decomposed into disjoint pieces, and it is a
cover, if the pieces are overlapping. While algorithms for convex decomposition
are well understood in 2-dimensional space, the same cannot be said about higher
dimensions [19]. In this work, we approximate the convex decomposition of an
arbitrary shape cluster by the convex polytopes generated by the Kmeans centers
that are within that cluster. Depending on the complexity of the shape, higher
number of centers may be required to obtain a good approximation of that shape.
Essentially, we can reformulate the original problem of identifying arbitrary shaped
clusters in terms of a sampling problem. Ideally, we want to minimize the number
of centers, with the constraint that the space covered by each center is a convex
polytope. One can immediately identify this optimization problem as a modified
version of the facility location problem. In fact, this optimization problem is exactly
the Minimum Consistent Subset Cover Problem (MCSC) [39]. Given a finite set
S and a constraint, the MCSC problem considers finding a minimal collection T
S
of subsets such that C∈T C = S, where C ⊂ S, and each C satisfies the given
constraint. In our case, S is the set of points and c the convex polytope constraint.
The MCSC problem is NP-hard, and thus finding the optimal centers is hard. We
thus rely on the iterative Kmeans type method to approximate the centers.
31
32
3.1
The SPARCL Algorithm
The pseudo-code for the SPARCL algorithm is given in Figure 3.1. The algo-
rithm takes two input parameters. The first one k is the final number of clusters
desired. We refer to these as the natural clusters in the dataset, and like most other
methods, we assume that the user has a good guess for k. In addition SPARCL
requires another parameter K, which gives the number of seed centers to consider
to approximate a good convex decomposition; we also refer to these seed centers as
pseudo-centers. Note that k < K ≪ n = |D|. Depending on the variant of Kmeans
used to obtain the seeds centers, SPARCL uses a third parameter mp, denoting the
number of nearest neighbors to consider during a smart initialization of Kmeans
that avoids outliers as centers. The random initialization based Kmeans does not
require the mp parameter.
SPARCL operates in two stages. In the first stage we run the Kmeans algorithm on the entire dataset to obtain K convex clusters. The initial set of centers
for the Kmeans algorithm may be chosen randomly, or in such a manner that they
are not outlier points. Following the Kmeans run, the second stage of the algorithm computes a similarity metric between every seed cluster pair. The resulting
similarity matrix can act as input either for a hierarchical or a spectral clustering
algorithm. It is easy to observe that this two-stage refinement employs a cheaper
(first stage) algorithm to obtain a course grained clustering. The first phase has
complexity O(ndKe), where d is the data dimensionality and e is the number of iterations Kmeans takes to converge, which is linear in n. This approach considerably
reduces the problem space as we only have to compute O(K 2 ) similarity values in
the second phase. For the second phase we can use a more expensive algorithm to
obtain the final set of k natural clusters.
SPARCL(D, K, k, mp):
1. Cinit = seed center initialization(D, K, mp)
2. Cseed = Kmeans(Cinit , K)
3. forall distinct pairs (Ci , Cj ) ∈ Cseed × Cseed
4.
S(i, j) = compute similarity(Ci , Cj )
5. cluster centers(Cseed , S, k)
Figure 3.1: The SPARCL Algorithm
33
3.2
Phase 1 – Kmeans Algorithm
The first stage SPARCL is shown in steps 1 – 2 of Figure 3.1. This stage
involves running the Kmeans algorithm with a set of initial centers Cinit (line 1),
until convergence, at which point we obtain the final seed clusters Cseed . There is one
subtlety in this step; instead of using the mean point in each iteration of Kmeans,
we actually use an actual data point in the cluster that is closest to the center mean.
We do this for two reasons. First, if the cluster centers are not actual points in the
dataset, chances are higher that points from two different natural clusters would
belong to a seed cluster, considering that the clusters are arbitrarily shaped. When
this happens, the hierarchical clustering in the second phase would merge parts
of two different natural clusters. Second, our approach is more robust to outliers,
since the mean point can get easily influenced by outliers. Figure 3.2(a) outlines an
example. There are two natural clusters in the form of the two rings. When we run a
regular Kmeans, using the mean point as the center representative, we obtain some
seed centers that lie in empty space, between the two ring-shaped clusters (e.g., 4, 5,
and 7). By choosing an actual data point, we avoid the “dangling” means problem,
and are more robust to outliers, as shown in Figure 3.2(b).
This phase starts by selecting the initial set of centers for the Kmeans algorithm. In order for the second stage to capture the natural clusters in the datasets,
it is important that the final set of seed centers, Cseed , generated by the Kmeans
algorithm satisfy the following properties:
1. Points in Cseeds are not outlier points,
2. Representatives in Cseed are spread evenly over the natural clusters.
In general, random initialization is fast, and works well. However, selecting the
centers randomly can violate either of the above properties, which can lead to illformed clusters for the second phase. Figure 3.3 shows an example of such a case.
In Figure 3.3(a) seed center 1 is almost an outlier point. As a result the members
belonging to seed center 1 come from two different natural clusters. This results in
the small (middle) cluster merging with the larger cluster to its right.
In order to avoid such cases and to achieve both the properties mentioned
34
4
5
7
2
1
8
3
6
(a) Using mean point
4
1
8
7
6
2
3
5
(b) Using actual data point
Figure 3.2: Effect of Choosing mean or actual data point
above we utilize our recently proposed outlier and density insensitive based selection
of initial centers [50]. Let us take a quick look at other initialization methods before
discussing our Local Outlier Factor based initialization technique.
3.2.1
Kmeans Initialization Methods
Although there are numerous initialization methods, we briefly discuss some
of the key ones. One of the first schemes of center initialization was proposed by
Ball and Hall [8]. They suggested use of a user defined threshold, d, to ensure that
the seed points are well apart from each others. The first point is chosen as a seed,
35
1.5
1
3
2
0.5
6
4
0
1
5
−0.5
−1
−2
−1.5
−1
−0.5
0
0.5
1
1.5
1
1.5
(a) Randomly selected centers
6 Centers
1.5
1
0.5
0
−0.5
−1
−2
−1.5
−1
−0.5
0
0.5
(b) Natural cluster split by bad center assignment
Figure 3.3: Bad Choice of Cluster Centers
and for any subsequent point considered, it is selected as a seed if it is at least d
distance apart from already chosen seeds, until k seeds are found. With a right
choice of the value of d, this approach can restrict the splitting of natural clusters,
but guessing a right value of d is very difficult and the quality of seeds depends on
the order in which the data points are considered.
Astrahan [7] suggested using two distance parameters, d1 and d2 . The method
first computes the density of each point in the dataset, which is given as the number
of neighboring points within the distance d1 , and it then sorts the data points
according to decreasing value of density. The highest density point is chosen as the
36
first seed. Subsequent seed point are chosen in order of decreasing density subject to
the condition that each new seed point be at least at a distance of d2 from all other
previously chosen seed points. This step is continued until no more seed points can
be chosen. Finally, if more than k seeds are generated from the above approach,
hierarchical clustering is used to group the seed points into the final k seeds. The
main problem with this approach is that it is very sensitive to the values of d1 and d2 .
Furthermore, users have insufficient knowledge regarding the good choices of these
parameters, and the method is computationally very expensive. A range search
query needs to be made for every data point followed by a hierarchical clustering of
a set of points. Small values of d1 and d2 may produces enormously large number of
seeds, and hierarchical clustering of those seeds can be very expensive (O(n2 log n)
in the worst case). This method also performs poorly when there exist different
clusters in the dataset with variable density and size.
Katsavounidis et. al. [57] suggested a parameterless approach, which we call
the KKZ method based on the initials of all the authors. KKZ chooses the first
centers near the “edge” of the data, by choosing the vector with the highest norm
as the first center. Then, it chooses the next center to be the point that is farthest
from the nearest seed in the set chosen so far. This method is very inexpensive
(O(kn)) and is easy to implement. It does not depend on the order of points and
is deterministic by nature; as single run suffices to obtain the seeds. However, KKZ
is sensitive to outliers, since the presence of noise at the edge of the dataset may
cause a small set of outlier/noise points to make up a cluster.
Bradley and Fayyad [14] proposed an initialization method that is suitable for
large datasets. We call their approach Subsample, since they take a small subsample
(less than 5%) of the dataset and use k-means clustering on the subsample and
record the cluster centers. This process is repeated and cluster centers from all the
different iterations are accumulated in a dataset. Finally, a last round of k-means
is performed on this dataset and the cluster centers of this round are returned as
the initial seeds for the entire dataset. This method generally performs better than
k-means and converges to the local optimal faster. However, it still depends on
the random choice of the subsamples and hence, can obtain a poor clustering in an
37
unlucky session.
More recently, Arthur and Vassilvitskii [6] proposed the k-means++ approach,
which is similar to the KKZ method. However, when choosing the seeds, they do
not choose the farthest point from the already chosen seeds, but choose a point with
a probability proportional to its distance from the already chosen seeds.
3.2.2
Initialization using Local Outlier Factor
We chose the local outlier factor (LOF) criterion for selecting the initial set of
cluster centers. LOF was proposed in [15] as a measure for determining the degree
to which a point is an outlier. For a point x ∈ D, define the local neighborhood of
x, given the minimum points threshold mp as follows:
N (x, mp) = {y ∈ D | dist(x, y) ≤ dist(x, xmp )}
where xmp is the mp-th nearest neighbor of x. Thus N (x, mp) contains at least mp
points. The density of x is then computed as follows:
density(x, mp) =
P
y∈N (x,mp) distance(x, y)
| N (x, mp) |
!−1
Essentially, the lower the distance between x and neighboring points, the higher the
density of x. The average relative density (ard) of x, is then computed as the ratio
of the density of x and the average density of its nearest neighbors, given as follows:
ard(x, mp) = P
density(x, mp)
density(y,mp)
|N (x,mp)|
y∈N (x,mp)
Finally the LOF score of x is just the inverse of the average relative density
of x:
LOF (x, mp) = ard(x, mp)−1
If a point is in a low density neighborhood compared to all its neighbors, then its
ard score is low and hence its LOF value is high. Thus LOF value represents the
extent to which a point is an outlier. A point that belongs to a cluster has an LOF
38
value approximately equal to 1, since its density and the density of its neighbors is
approximately the same.
LOF has three excellent properties: (1) It is very robust when the dataset has
clusters with different sizes and densities. (2) Even though the LOF value may vary
somewhat with mp, it is generally robust in making the decision whether a point is
an outlier or not. That is, for a large range of values of mp, the outlier points will
have LOF value well above 1, whereas points belonging to a cluster will assume an
LOF value close to 1. (3) It leads to practically faster convergence of the Kmeans
algorithm, i.e., fewer iterations.
As we reported in [50], to select the initial seeds, we use the following approach.
A non-outlier point with the largest norm is selected as the first center. The largest
norm ensures that the selected center is farthest from the origin. For selecting
subsequent centers assume that i initial centers have been chosen. To choose the
i + 1-th center, we first compute the distance of each point to each of the i chosen
centers, and sort them in decreasing order of distance. Next, in that sorted order,
we pick the first point that is not an outlier as the next seed. We repeat until K
initial seeds have been chosen, and then run the Kmeans algorithm to converge with
those initial starting centers, to obtain the final set of seed centers Cseed .
3.2.3
Complexity Analysis of LOF Based Initialization
The overall complexity of this approach can be analyzed in terms of the steps
involved. Let us assume that t ≪ n is the number of outliers in the data. While
choosing the i + 1-th center, the minimum distance of each of the n − i non-center
points from the i centers is computed. Aggregated over the K centers, the total
computational cost of this step amounts to O(nK 2 d), where d is the dimensionality
of the data. Once the minimum distances are computed, the i + 1-th center is chosen by examining points in descending order of minimum distance and selecting the
point that has an LOF value close to 1. The linear-time partition-based selection
algorithm [22] for computing the p-th largest number can be used to find the points
in descending order. In the worst case, the selection algorithm has to be invoked t
times (with p = 1 . . . t) for the i + 1-th center selection. If t is a small constant, the
39
selection based approach can be much more efficient as compared to the O(n log n)
sorting based selection algorithm. The aggregated computational cost for the selection phase of K centers is given by O(tnK) or O(tKn log n) in the worst case.
The LOF value for each examined point is computed during the selection stage.
1
The cost of computing the LOF value of a point is given by O(n1− d ∗ mp), since
nearest neighbor queries are performed on the mp neighbors of the point and each
1
nearest neighbor query takes O(n1− d ) time. In the worst case, for each center t
LOF computations need to be performed. As the result, the LOF computation
1
aggregated over K centers comes out to O(n1− d ∗ mp ∗ t ∗ K). Finally, adding
up the costs of the above steps, the complexity of the entire process is given by
1
O(nK 2 d + tKn log n + n1− d ∗ mp ∗ t ∗ K). As seen from the previous expression, the
overall time complexity is linear in the number of points in the data. On the other
hand, a random initialization for the seed centers takes O(K) time. As an example
350
5
300
19 47
29
37 25
42 18 23 49
46
11 31
10
7
12
39
30
27
13
28 21 38
26
44
24 32 1
2 50 41 48 20
34
17 8 45
9
22
36 4
16
43
250
200
150
100
50
0
6
14 33 3 35 15
40
0
100
200
300
400
500
600
700
(a) Selected centers on D1 dataset
Figure 3.4: Local Outlier Based Center Selection
of LOF-based seed selection, Figure 3.4 shows the initial set of centers for one of
the shape-based datasets. Section 3.6.2 provides an empirical comparison of LOF
based initialization with other initialization methods.
40
3.3
Phase 2 – Merging Neighboring Clusters
As the output of the first phase of the algorithm, we have a relatively small
number K of seed cluster centers (compared to the size of the dataset) along with
the point assignments for each cluster. During the second phase of the algorithm,
a similarity measure for each pair of seed clusters is computed (see lines 3-4 in
Figure 3.1). The similarity between clusters is then used to drive any clustering
algorithm that can use the similarity function to merge the K seed clusters in the
final set of k natural clusters. We applied both hierarchical as well as spectral
methods on the similarity matrix. Since the size of the similarity matrix is O(K 2 ),
as opposed to O(n2 ), even spectral methods can be conveniently applied.
p
p
p
j
i
k
Vk
B Xu
B X2 B
X1
11
00
00
11
Ii
Center X
fx
B Y0 B
Y1 B Y2 B Y3
B X0
Ij
B Yv
1
0
0
1
Center Y
fy
Hk
Figure 3.5: Projection of points onto the vector connecting the centers
3.3.1
Cluster Similarity
Let us consider that the d-dimensional points belonging to a cluster X are
denoted by PX and similarly points belonging to cluster Y are denoted by PY . The
corresponding centers are denoted by cX and cY , respectively. A similarity score
is assigned to each cluster pair. Conceptually, each cluster can be considered to
41
represent a Gaussian and the similarity captures the overlap between the Gaussians. Intuitively, two clusters should have a high similarity score if they satisfy the
following conditions:
1. The clusters are close to each other in the Euclidean space.
2. The densities of the two clusters are comparable, which implies that one cluster
is an extension of the other.
3. The face (hyperplane) at which the clusters meet is wide.
The compute similarity function in Figure 3.1 computes the similarity for a given
pair of centers. For computing the similarity, points belonging to the two clusters
are projected on the vector connecting the two centers as shown in Figure 3.5. Even
though the figure just shows points above the vector being projected, this is merely
for the convenience of exposition and illustration. fx represents the distance from
the center X to the farthest projected image Ii of a point pi belonging to X. Hi is
the horizontal (along the vector joining the two centers) distance of the projection
of point pi from the center, and Vi is the perpendicular (vertical) distance of the
point from its projection. The means (mHX and mHY ) and standard deviations
(sHX and sHY ) of the horizontal distances for points belonging to the clusters are
computed. Similarly, means and standard deviations for perpendicular distances are
computed. A histogram with bin size of
si
2
(i ∈ {HX , HY }) is constructed for the
projected points. The bins are numbered starting from the farthest projected point
fi (i ∈ X, Y ), i.e., bin BX0 is the first bin for the histogram constructed on points
in cluster X. The number of bins for cluster X is given by |BX |. Then, we compute
the average of horizontal distances for points in each bin; dij denotes the average
distance for bin j in cluster i. max bini = arg maxj dij represents the bin with the
largest number of projected points in cluster i. The number of points in bin Xi is
given by N [Xi ]. The ratio
N [Xi ]
N [Xmax binX ]
is denoted by sz ratioXi .
Now, the size based similarity between two bins in clusters X and Y is given
by the equation:
size sim(BXi , BYj ) = sz ratio(BXi ) ∗ sz ratio(BYj )
(3.1)
42
The distance-based similarity between two bins in clusters X and Y is given by the
following equation, where dist(BXi , BYj ) is the horizontal distance between the bins
Xi and Yj :
dist sim(BXi , BYj ) =
2 ∗ dist(BXi , BYj )
sHX + sHY
(3.2)
The overall similarity between the clusters X and Y is then given as
S(X, Y ) =
t
X
size sim(BXi , BYi ) ∗ exp−dist sim(BXi ,BYi )
(3.3)
i=0
where t = min(|BX |, |BY |). Also, while projecting the points onto the vector, we
discarded points that had a vertical distance greater than twice the vertical standard
deviation, considering them as noise points.
Let us look closely at the above similarity metric to understand how it satisfies
the above mentioned three conditions for good cluster similarity. Since the bins start
from the farthest projected points, for bordering clusters the distance between X0
and Y0 will be very less. This gives a small value to dist sim(BX0 , BY0 ). As a result,
the exponential function gets a high value due to the exponent taking a low value.
This causes the first term of the summation in Equation 3.3 to be high, especially if
the size sim score is also high. A high value for the first term indicates that the two
clusters are close by and that there are a large number of points along the surface of
intersection of the two clusters. If the size sim(BX0 , BY0 ) is small, which can happen
when the two clusters meet at a tangent point, the first term in the summation will
be small. This is exactly as expected intuitively and captures conditions 1 and 3
mentioned above. Both the size sim and dist sim measures are averse to outliers
and would give a low score for bins containing outlier points. For outlier bins, the
sz ratio will have a low score, resulting in a lower score for size sim. Similarly,
clusters having outlier points would tend to have a high standard deviation, which
would result in a low score for dist sim.
We considered the possibility of extending the histogram to multiple dimensions, along the lines of grid-based algorithms [40], but the additional computational
cost does not justify the improvement in the quality of the results.
43
Finally, once the similarity between pairs of seed has been computed, we can
use spectral or hierarchical agglomerative clustering to obtain the final set of k natural clusters. For our experiments, we used the agglomerative clustering algorithm
provided with CLUTO.
Our similarity metric S(X, Y ) can be shown to be a kernel. The following
lemmas regarding kernels allow us to prove that the similarity function is a kernel.
Lemma 3.3.1 [103] Let κ1 and κ2 be kernels over X × X, X ⊆ Rn , and let f (.) be
a real-valued function on X. Then the following functions are kernels:
i. κ(x, z) = κ1 (x, z) + κ2 (x, z),
ii. κ(x, z) = f (x)f (z),
iii. κ(x, z) = κ1 (x, z)κ2 (x, z),
Lemma 3.3.2 [103] Let κ1 (x, z) be a kernel over X × X, where x, z ∈ X. Then
the function κ(x, z) = exp(κ1 (x, z)) is also a kernel.
Theorem 3.3.3 Function S(X, Y ) in Equation 3.3 is a kernel function.
Proof: Since dist and sz ratio are real valued functions, dist sim and size sim are
kernels by Lemma 3.3.1(ii). This makes exp(−dist sim(., .)) a kernel by Lemma 3.3.2.
Product of size sim and exp(−dist sim(., .)) is a kernel by Lemma 3.3.1(iii). And finally, S(X, Y ) is a kernel since the sum of kernels is also a kernel by Lemma 3.3.1(i).
qededtrue
The matrix obtained by computing S(X, Y ) for all pairs of clusters turns out to
be a kernel matrix. This nice property provides the flexibility to utilize any kernel
based method, such as spectral clustering [88] or kernel k-means [29], for the second
phase of SPARCL.
3.4
Complexity Analysis
The first stage of SPARCL starts with computing initial K centers randomly
or based on the local outlier factor. If we use random initialization phase 1 takes
44
O(Knde) time, where e is the number of Kmeans iterations. The time for computing
1
the LOF-based seeds is O(nK 2 d + tKn log n + n1− d ∗ mp ∗ t ∗ K) [50], where t is the
number of outliers in the dataset, followed by the O(Knde) time for Kmeans. The
second phase of the algorithm projects points belonging to every cluster pair on the
vector connecting the centers of the two clusters. The projected points are placed
in appropriate bins of the histogram. The projection and the histogram creation
requires time linear in the number of points in the seed cluster. For the sake of
simplifying the analysis, let us assume that each seed cluster has the same number
of points,
n
.
K
Projection and histogram construction requires O( Kn ) time. In practice
only points from a cluster that lie between the two centers are processed, reducing
the computation by half on an average. Since there are O(K 2 ) pairs of centers,
the total complexity for generating the similarity map is K 2 × O( Kn ) = O(Kn).
The final stage applies a hierarchical or spectral algorithm to find the final set of
k clusters. Spectral approach will take O(K 3 ) time in the worst case, whereas
agglomerative clustering will take time O(K 2 log K). Overall, the time for SPARCL
is O(Knd + K 2 log K) (ignoring the small number of iterations it takes Kmeans
to converge) if using the random initialization, or O(K 2 nd + K 2 log K), assuming
mp = O(K), and using the LOF-based initialization. In our experiment evaluation,
we obtained comparable results using random initialization for datasets with uniform
density of clusters. With random initialization, the algorithm runs in time linear in
the number of points as well as the dimensionality of the dataset.
3.5
Estimating the Value of K
As discussed in Section 3.3, neighboring clusters are merged to obtain the
final set of k natural clusters. A “good” clustering is guaranteed if the following
conditions are satisfied:
1. Merging Condition – Only pseudo-centers belonging to a single natural
cluster are merged together,
2. Pseudo-center Condition – No pseudo-center exists such that it is a representative for points belonging to more than one natural cluster.
45
The Merging Condition is influenced by the effectiveness of the similarity measure
and the merging process itself. The similarity score in turn depends on the satisfiability of the Pseudo-center Condition. This transitive dependence between the
above two conditions indicates that satisfying the second condition is crucial for
obtaining a good clustering result.
The value of K can adversely influence the Pseudo-center condition. Underestimating K can result in points from two or more natural clusters being assigned to
the same pseudo-center, since each center has to now account for a larger number
of points. This is emphasized by our results (Section 3.6.3.5) in Figure 3.18, which
shows a lower clustering quality score for smaller values of K. Hence, having a good
estimate of K can considerably improve the clustering quality. At the same time,
the clustering outcome is not sensitive to small changes in the value of K, which
implies that a rough estimate suffices.
In many application domains the expert has an insight into approximate distances between natural clusters. For instance, cell biologists might have an estimate
of the distance between nearby chromosomes; a radiologist might have an intuition
regarding average distance between bones in an X-ray image; or distance between
regions of interest on a weather forecast map might be known a priori. Let us assume that an expert can estimate the minimum distance between any true clusters,
denoted by cdistmin . Given cdistmin , we can estimate the value of K such that
the Pseudo-center Condition is satisfied. Figure 3.6(a) shows the true clusters for
an illustrative dataset, with the noise points removed. The figure also shows the
cdistmin for this dataset.
Assume point A is selected as one of the pseudo-centers. In order to assign
point B to a center other than A, there has to be another center C closer than
cdistmin to point B. Any point closer than cdistmin to B has to belong to Cluster
1, which implies that center C would belong to Cluster 1. In other words, if the
nearest center for each point is at a distance less than cdistmin , condition two is satisfied. If the dataset is scattered over a 2-dimensional region with area (volume for
V
higher dimensions) V , then the value of K is given by ⌈ 2πcdist
⌉. The 2πcdistmin
min
expression is an approximation for the area of a circle (convex polyhedron) around
46
B
cdistmin
A
CLUSTER 2
CLUSTER 1
(a) Estimating K from cdistmin
300
300
250
200
150
9
12
8
250
16
20
10 24
200
1
26 6
7
14
18
150
15
2
100
22
23
4
3
19
50
0
400
21
13
17
11
420
440
460
480
500
(b) Seed Centers with
100
5
25
50
520
540
560
cdistmin = 20
580
0
400
420
440
460
480
500
520
540
560
580
(c) Members of each seed cluster with cdistmin =
20
Figure 3.6: Estimating the value of K
a center point. The above expression can be similarly generalized for higher dimensional datasets to ⌈ V ol.
V ol. occupied by cluster shape
⌉.
of hypersphere with radius cdistmin
The area or volume occupied
by the clusters does not have to be computed explicitly. Based on the above idea,
the LOF based algorithm (Section 3.2) for obtaining initial seeds can be modified
to automatically select the required number of seeds. Figure 3.7 shows the modified
47
LOF initialization algorithm. The algorithm seed center initialization takes as
input the dataset of points D, cdistmin and a parameter for LOF computation. The
algorithm returns the set of seed pseudo-centers. In the LOF based initialization, it
seed center initialization(D, cdistmin , mp):
1. Take any reference point, r (origin suffices)
2. Insert r in C
3. do
4.
sort the points in D in decreasing order of
5.
minimum distance from points in C
6.
for each x in sorted order
7.
if (LOF(x, mp) ≈ 1)
8.
insert x in C
9.
min dist = distx
10.
break
11.
endif
12.
endfor
13. while min dist ≥ cdistmin
14. remove r from C
15. return C
Figure 3.7: Generating seed representatives with cdistmin
can be shown that each subsequently selected seed representative results in a monotonic decrease in the minimum distance (min dist). As a result, the condition on
Line 13 is violated after a finite number of iterations of the while loop. At the time
the condition in the while loop is violated, the maximum distance of a point to its
nearest seed representative is less than cdistmin . As a result of which, no pseudocluster has points from more than one natural cluster. The LOF function on Line
7 computes the Local Outlier Factor for a point. Recall that the LOF value is an
indicator of the degree to which a point is an outlier. A value close to 1 signifies a
point is not an outlier.
We would like to caution the reader that this is a worst case analysis which
guarantees that the Pseudo-center Condition is satisfied. On the downside, for
pathological datasets much larger number of seed representatives could be selected
(in the worst case O(n) seeds) as compared to what might suffice for a good clustering. This can be seen in the results for dataset DS2 wherein a good clustering is
obtained with K = 60 (as shown in Figure 3.9(b)). Applying the algorithm in Fig-
48
ure 3.7 generates K = 287 seed representatives with cdistmin = 20. For the dataset
in Figure 3.6(a), the seed centers and the points assigned to them are shown in Figures 3.6(b) and 3.6(c), respectively. As one can see in Figure 3.6(b), the LOF based
initialization generates centers that are uniformly distributed. For regular shaped
clusters, the Pseudo-center Condition can be preserved even with a non-uniform
distribution of the centers as long as points such as A and B are not assigned to
the same seed-cluster. This approach could result in a reduced number of seed centers and a faster overall computation time. In this work, we do not address the
non-uniform selection of seed centers.
3.6
Experiments and Results
Experiments were performed to compare the performance of our algorithm
with Chameleon [64], DBSCAN [34] and spectral clustering [105]. The Chameleon
code was obtained as a part of the CLUTO [127]7 package. The DBSCAN implementation in Weka was used for the sake of comparison. Similarly, for spectral
clustering the SpectraLIB Matlab implementation
8
based on the Shi-Malik algo-
rithm [105] was used initially. Since this implementation could not scale to larger
datasets, we implemented the algorithm in C++ using the GNU Scientific Library9
and SVDLIBC10 . Even this implementation would not scale to very large datasets
since the entire affinity matrix would not fit in memory. The results in Table 3.2
for spectral clustering are based on this implementation.
Even though the implementations are in different languages, some of which
might be inherently slower than others, the speedup due to our algorithm far surpasses any implementation biases. All the experiments were performed on Mac G5
machine with a 2.66 GHz processor, running the Mac 10.4 OS X. Our code is written
in C++ using the Computational Geometry Algorithms Library (CGAL). We show
results for both LOF based as well as random initialization of seed clusters.
7
http://glaros.dtc.umn.edu/gkhome/cluto/
http://www.stat.washington.edu/spectral/
9
http://www.gnu.org/software/gsl/
10
http://tedlab.mit.edu/~dr/svdlibc/
8
49
3.6.1
Datasets
3.6.1.1
Synthetic Datasets
We used a variety of synthetic and real datasets to test the different methods.
DS1, DS2, DS3, and DS4, shown in Figures 3.9(a), 3.9(b), 3.9(c), and 3.9(d), are
those that have been used in previous studies including Chameleon and CURE.
These are all 2D datasets with points ranging from 8000 to 100000. The Swissroll dataset in Figure 3.10 is the classic non-linear manifold using in non-linear
dimensionality reduction [74]. We simply split the manifold into four clusters to see
how our methods handle this case.
For the scalability tests, and for generating 3D datasets, we wrote our own
shape-based cluster generator. To generate a shape in 2D, we randomly choose
points in the drawing canvas and accept the points which lie in our desired shape.
All the shapes are generated with point (0,0) as the origin. To get complex shapes,
we combine rotated and translated basic shapes (circle, rectangle, ellipse, circular
strip, etc.). Our 3D shape generation is built on the 2D shapes. We randomly
choose points in the 3 coordinates, if the x and y coordinates satisfy the shape, we
randomly choose the z-axis from a given range. This approach generates true 3D
shapes, and not only layers of 2D shapes. Similar to the case for 2D, we combine
rotated and translated basic 3D shapes to get more sophisticated shapes. Once we
generate all the shapes, we randomly add noise (1% to 2%) to the drawing frame.
An example of a synthetic 3D dataset is shown in Figure 3.13(b). This 3D dataset
has 100000 points, and 10 clusters.
3.6.1.2
Real Datasets
We used two real shape-based datasets: cancer images and protein structures.
The first is a set of 2D images from benign breast cancer
11
. The actual images are
divided into 2D grid cells (80 × 80) and the intensity level is used to assign each
grid to either a cell or background. The final dataset contains only the actual cells,
along with their x and y co-ordinates.
Proteins are 3D objects where the coordinates of the atoms represent points.
11
These were obtained from Prof. Bulet Yener at RPI
50
Since proteins are deposited in the protein data bank (PDB) in different reference
frames, the coordinates of the protein need to be centered such that the minimum
point (atom) is above the (0,0,0) origin. We translate the proteins to get separated
clusters. Once the translation is done, we add the noise points. Our protein dataset
has 15000 3D points obtained from the following proteins: 1A1T (865 atoms), 1B24
(619 atoms), 1DWK (11843 atoms), 1B25 (1342 atoms), and 331 noise points.
3.6.2
Comparison of Kmeans Initialization Methods
We compared different initialization methods on a set of synthetic datasets.
These datasets contain regular shaped clusters of varying sizes and densities. The
exact details of the datasets are omitted as they do not influence the comparative
results. Since the clusters generated by Kmeans are hyperspheres, distortion score
is used as the evaluation metric for comparing the initialization methods. Distortion
Score is defined as the sum of the distance between each point and its closest center.
Smaller value of distortion implies a better clustering.
Multiple runs are performed for algorithms that depend either on the order of
objects in the dataset or on randomization. For those algorithms, the minimum and
average distortion values are shown. Results for different dimensions (d) and number
of natural clusters (k) are shown in Table 3.1. The value in bold indicates the best
result for each row. The optimal distortion measure is also shown since the datasets
are synthetically generated. The results show that the LOF based initialization
performs better on most of the datasets.
Results in Figure 3.8 highlight the
robustness of LOF-based initialization as compared to random initialization. In
Figure 3.8(a), the distortion score is computed for varying percentage of random
noise in the dataset. Again, a lower distortion score indicates robustness to random
noise. Similarly, Figure 3.8(b) shows that the LOF based initialization is robust to
small changes in the parameter (mp) value.
3.6.3
Results on Synthetic Datasets
Results of SPARCL on the synthetic datasets are shown in Table 3.2, and
in Figure 3.9 and 3.10. We refer the reader to [64] for the clustering results of
Chameleon and DBSCAN on datasets DS1-4. In essence, Chameleon is able to
51
d
k Optimal
8 10
25
50
16 10
25
50
24 10
25
50
7738
9365
8694
16865
17241
17580
26149
22233
21453
LOF
7755
9382
8754
16882
17261
17622
26150
22261
21467
Random
min
avg
7904 8421
9774 10185
9244 9565
17406 18496
18298 19219
18866 19507
26706 28733
23241 24582
22838 23818
Subsample
min
avg
7887 8092
9639 10044
9136 9407
17356 18314
17647 18812
18469 19084
26150 28340
23034 23942
22477 23387
k-means++
min
avg
8008 8508
9641 9951
9289 9598
16870 17951
17732 18550
18974 19661
26755 28860
22803 23787
23003 23762
KKZ
9204
10743
17042
19346
20567
21632
29413
27052
26599
Table 3.1: Comparison on synthetic datasets. The distortion scores are
shown for each method. The value in bold indicate the best
result for each row.
LOF
Random minimum
Random average
Random maximum
6300
Distortion Score
Distortion Score
8000
6400
LOF
random minimum
random average
random maximum
7600
7200
6200
6100
6000
5900
5800
5700
2
4
6
Noise percentage
(a) Random Noise
8
10
5
10
15
20
25
mp value
30
35
40
(b) d = 8, k = 15
Figure 3.8: Sensitivity Comparison: LOF vs. Random
Name
|D|(d)
DS1
8000 (2)
DS2
10000 (2)
DS3
8000 (2)
DS4
100000 (2)
Swiss-roll 19200 (3)
k
6
9
8
5
4
SPARCL
Chameleon DBSCAN Spectral
(LOF/Random)
5.74/1.277
4.02
14.16
199
8.6/1.386
5.72
24.2
380
6.88/1.388
4.24
14.52
239
35.24/20.15
280.47
23.92/17.89
19.38
-
Table 3.2: Runtime Performance on Synthetic Datasets. All times are
reported in seconds. ‘-’ for DBSCAN and Spectral method
denotes the fact that it ran out of memory for all these cases.
52
(a) Results on DS1
(b) Results on DS2
(c) Results on DS3
(d) Results on DS4
Figure 3.9: SPARCL clustering on standard synthetic datasets from the
literature.
perfectly cluster these datasets, whereas both DBSCAN and CURE make mistakes,
or are very dependent on the right parameter values to find the clusters. As we
can see SPARCL had no difficulty in identifying the shape-based clusters in these
datasets. However, SPARCL does make minor mistakes at the boundaries in the
Swiss-roll dataset (Figure 3.10). The reason for this is that SPARCL is designed
mainly for full-space clusters, whereas this is a 2D manifold embedded in a 3D
space. In other words, it is a nonlinear subspace cluster. What is remarkable is that
53
Figure 3.10: Results on Swiss-roll
SPARCL can actually find a fairly good clustering even in this case.
Table 3.2 shows the characteristics of the synthetic datasets along with their
running times. The default parameters for running Chameleon in CLUTO were retained (number of neighbors was set at 40). Parameters that were set for Chameleon
include the use of graph clustering method (clmethod=graph) with similarity set to
inverse of Euclidean distance (sim=dist) and the use of agglomeration (agglofrom=30),
as suggested by the authors. Results for both the LOF and random initialization
are presented for SPARCL. Also, we used K = 50, 60, 70, 50 for each of the datasets
DS1-4, respectively. For swiss-roll we use K = 530.
We can see that DBSCAN is 2-3 times slower than both SPARCL and Chameleon
on smaller datasets. However, even for these small datasets, the spectral approach
ran out of memory. The times for SPARCL (with LOF) and Chameleon are comparable for the smaller datasets, though the random initialization gives the same
results and can be 3-4 times faster. For the larger DS4 dataset SPARCL shows an
order of magnitude faster performance, showing the real strength of our approach.
For DBSCAN we do not show the results for DS4 and Swiss-roll since it returned
only one cluster, even when we played with different parameter settings.
Time (sec)
54
40000
35000
30000
25000
20000
15000
10000
5000
0
SPARCL(random)
SPARCL(lof)
Chameleon
DBScan
0
100 200 300 400 500 600 700 800 900 1000
# of points x 1000 (d=2)
Figure 3.11: Scalability Results on Dataset DS5
3.6.3.1
Scalability Experiments
Using our synthetic dataset generator, we generated DS5, in order to perform
experiments on varying number of points, varying densities and varying noise levels.
For studying the scalability of our approach, different versions of DS5 were generated
with different number of points, but keeping the number of clusters constant at 13.
The noise level was kept at 1% of the dataset size. Figure 3.11 compares the runtime
performance of Chameleon, DBScan and our approach for dataset sizes ranging from
100000 points to 1 million points. We chose not to go beyond 1 million as the time
taken by Chameleon and DBSCAN was quite large. In fact, we had to terminate
DBSCAN beyond 100K points. Figure 3.11 shows that our approach, with random
initialization, is around 22 times faster than Chameleon while it is around 12 time
faster when LOF based initialization is considered. Note that the time for LOF also
increases with increase in the size of the dataset. For Chameleon, the parameters
agglofrom, sim, clmethod were set to 30, dist and graph, respectively. For DBSCAN
the eps was set at 0.05 and MinPts was set at 150 for the smallest dataset. MinPts
was increased linearly with the size of the dataset. In our case, for all datasets,
55
K = 100 seed centers were selected for the first phase and mp was set to 15.
(a) SPARCL (K = 100)
(b) DBSCAN (minPts=150, eps=0.05)(c)
Chameleon
(agglofrom=30,
sim=dist, clmethods=graph)
Figure 3.12: Clustering Quality on Dataset DS5
Figure 3.12 shows the clusters obtained as a result of executing our algorithm,
DBSCAN and Chameleon on the dataset DS5 of size 50K points. We can see that
DBSCAN makes the most mistakes, whereas both SPARCL and Chameleon do well.
Scalability experiments were performed on 3D datasets as well. Result for one
of those datasets is shown in Figure 3.13(b). The 3D dataset consists of shapes in
full 3D space (and not 2D shapes embedded in 3D space). The dataset contained
random noise too (2% of the dataset size). As seen in Figure 3.13(a), SPARCL
(with random initialization) can be more than four times as fast as Chameleon.
Time (sec)
56
20000
SPARCL(lof)
18000
16000 SPARCL(random)
Chameleon
14000
12000
10000
8000
6000
4000
2000
0
0
100
200
300
400
500
600
# of points x 1000 (d=3)
Figure 3.13: Clustering Results on 3D Dataset
3.6.3.2
Clustering Quality
Since two points in the same cluster can be very far apart, traditional metrics such as cluster diameter, k-Means/k-Medoid objective function (sum of squared
errors) and compactness (avg. intra-cluster distance over the avg. inter-cluster distance) are generally not appropriate for shape-based clustering. We apply supervised
57
metrics, wherein the true clustering is known apriori, to evaluate clustering quality.
Popular supervised metrics include purity, Normalized Mutual Information, rank
index, and so on. In this work, we use purity as the metric of choice due to its intuitive interpretation. Given the true set of clusters (referred to as classes henceforth
to avoid confusion), CT = {c1 , c2 , . . . , cL } and the clusters obtained from SPARCL
CS = {s1 , s2 , . . . , sM }, purity is given by the expression:
purity(CS , CT ) =
1 X
max ksk ∩ cj k
N k j
(3.4)
where N is the number of points in the dataset. Purity lies in the range [0,1], with
a perfect clustering corresponding to purity value of 1.
As a side note, purity tends to favor larger number of clusters, reaching a score
of 1 even when each point is in its own cluster. To overcome this bias Normalized
Mutual Information (NMI) [81] is used as a metric for clustering quality. Normalized
Mutual Information is given by the expression:
N M I(CS , CT ) =
I(CS ; CT )
[H(CS ) + H(CT )]/2
(3.5)
where I(CS ; CT ) is the mutual information and H(.) is the entropy. The mutual
information is given
I(CS , CT ) =
X X
p(si , cj ) log
si ∈CS cj ∈CT
and the entropy is given by H(X) = −
P
i∈X
p(si , cj )
p(si ) · p(cj )
(3.6)
p(i) log p(i). Since entropy increases
with the increase in number of clusters, overall NMI score decreases with increase
in the number of clusters. NMI overcomes this shortcoming of the purity measure
while maintaining the [0,1] range of the score. In our case, the number of clusters
obtained from SPARCL are the same as the true number of clusters. As a result,
purity can be safely used as the quality score without being concerned about the
above mentioned drawback.
Since DS1-DS4 and the real datasets do not provide the class information,
experiments were conducted on varying sizes of the DS5 dataset. The class infor-
58
mation was recorded during the dataset generation. Fig. 3.14 shows the purity score
for clusters generated by SPARCL and CHAMELEON (parameters agglofrom=100,
sim=dist, clmethod=graph). Since these algorithms cluster noise points differently,
for fair comparison they are ignored while computing the purity, although the noise
points are retained during the algorithm execution. Note that for datasets larger
than 600K, CHAMELEON did not finish in reasonable time. When CHAMELEON
was run with the default parameters, which runs much faster, the purity score lowered to 0.6, whereas SPARCL’s purity score is more than 0.9.
Purity score
1
0.9
0.8
0.7
0.6
Sparcl(lof)
Chameleon
0.5
0
100 200 300 400 500 600 700 800 900 1000
Dataset Size (x1000)
Figure 3.14: Clustering quality for varying dataset size
3.6.3.3
Varying Number of Clusters
Experiments were conducted to see the impact of varying the number of natural clusters k. To achieve this, the DS5 dataset was replicated by tiling the dataset
in a grid form. Since the DS5 dataset contains 13 natural clusters, a 1 × 3 tiling contains 39 natural clusters (see Fig. 3.15(a)). The number of points are held constant
at 180K. The number of natural clusters are varied from 13 to 117. The number of
seed-clusters are set at 5 times number of natural clusters, i.e, K = 5k. We see that
SPARCL finds most of the clusters correctly, but it does make one mistake, i.e., the
center ring has been split into two. Here we find that since there are many more
clusters, the time to compute the LOF goes up. In order to obtain each additional
center the LOF method examines a constant number of points, resulting in a linear
59
2500
SPARCL(lof)
SPARCL(random)
Chameleon
Time (sec)
2000
1500
1000
500
0
0
(a) 1x3 grid tiling. Results of SPARCL
20
40
60
80
100
# of natural clusters (d=2)
120
(b) Varying number of natural clusters.
Figure 3.15: Varying Number of Natural Clusters
relation between the number of clusters and the runtime. Thus we prefer to use the
random initialization approach when the number of clusters are large. With that
SPARCL is still 4 times faster than Chameleon (see Fig. 3.15(b)).
Even though Chameleon produces results competent with that of SPARCL, it requires tuning the parameters to obtain these results. Especially when the nearest
neighbor graph contains disconnected components CHAMELEON tends to break
natural clusters in an effort to return the desired number of clusters. Hence CHAMELEON expects the user to have a certain degree of intuition regarding the dataset
in order to set parameters that would yield the expected results.
3.6.3.4
Varying Number of Dimensions
Synthetic data generator SynDECA (http://cde.iiit.ac.in/~soujanya/
syndeca/) was used to generate higher dimensional datasets. The number of points
and clusters were set to 500K and 10, respectively. 5% of the points were uniformly
distributed as noise points. SynDECA can generate regular (circle, ellipse, square
and rectangle) as well as random/irregular shapes. Although SynDECA can generate subspace clusters, for our experiments full dimensional clusters were generated.
Fig. 3.16(b) shows the runtime for both LOF based and random initialization of
seed clusters. With increasing number of dimensions, LOF computation takes substantial time. This effect can be attributed to a combination of two effects. First,
1.1
3000
1
2500
0.9
2000
Time (sec)
Purity score
60
0.8
0.7
0.5
4
6
8
1500
1000
500
SPARCL(lof)
SPARCL(random)
Chameleon
0.6
SPARCL(lof)
SPARCL(random)
Chameleon
0
10
12
# of dimensions
(a) Purity
14
16
4
6
8
10
12
14
16
# of dimensions
(b) Runtime
Figure 3.16: Varying Number of Dimensions
since a kd-tree is used for nearest-neighbor queries the performance degrades with
increasing dimensionality. Second, since we keep the number of points constant in
this experiment, the sparsity of the input space increases for higher dimensions. On
the other hand, random initialization is computationally inexpensive. Fig. 3.16(a)
shows the purity for higher dimensions. Both SPARCL and CHAMELEON perform
well on this measure. The quality of the clustering can also be visually inspected.
The points in the high dimensional space can be projected onto a lower dimensional
space. For our experiments, we use Principal Component Analysis [32] (PCA) as
the dimensionality reduction technique. PCA has the distinction of being a linear
transformation that is optimal for preserving the subspace with the largest variance
in the data. Figure 3.17 shows the above dataset with 10 dimensions projected onto
a 3-dimensional subspace. The noise points have been purposely suppressed in order
to view the projected clusters clearly. As seen in Figure 3.17, the compact regions
representing the clusters contain points from the same natural clusters. Projecting
points on a lower dimensional sub-space, results in small overlap of some of the
clusters.
61
Figure 3.17: 10 dimensional dataset (size=500K, k=10) projected onto a
3D subspace
1
0.9
0.8
Purity score
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0
60
120 180 240 300 360 420 480 540
K
Figure 3.18: Clustering quality for varying number of seed-clusters
3.6.3.5
Varying Number of Seed-Clusters (K)
SPARCL has a single parameter, K. Fig. 3.18 shows the effect of changing K
on the quality of the clustering. The dataset used is same as in Fig. 3.15(a), with
300K points. As seen in the figure, the purity stabilizes around K=180 and remains
almost constant till K=450. As K is increased further, a significant number of seedcenters lie between two clusters. As a result SPARCL tends to merge parts of one
62
cluster with the other, leading to a gradual decline in the purity. Overall, the figure
shows that SPARCL is fairly insensitive to the K value.
100
90
80
70
60
50
40
30
20
10
0
200
100
0
200
180
160
140
120
100
80
60
40
20
0
Figure 3.19: Protein Dataset
3.6.4
Results on Real Datasets
We applied SPARCL on the protein dataset. As shown in Figure 3.19, SPARCL
is able to perfectly identify the four proteins. The largest doughnut-shaped is the
1DWK protein while the other smaller ones are amoeba like irregular shaped. The
K value for the protein dataset is 30. On this dataset, Chameleon returns similar results. The results on the benign cancer datasets are shown in Figure 3.21.
Here too SPARCL successfully identifies the regions of interest. The K value for
this dataset is 100. The distinct clusters in the cancer dataset represent the nuclei,
whereas the surrounding region is the tissue. Clusters that are globular in shape
correspond to healthy tissues whereas irregular shapes of the nuclei correspond to
cancerous tissues. We do not show the time for the real datasets since the datasets
are fairly small and both Chameleon and SPARCL perform similarly.
63
−1
−1
−1
50
−1
0
15
−1
10
−1
5
−1
0
−1
−5
15
−1
10
5
−10
−1
0
−5
−15
−10
−1
−2.5
−2
−1.5
−1
−0.5
0
0.5
1
1.5
2
−15
(a) Original Swiss-roll dataset
90
(b) Swiss roll embedded in 2D with
l=8
0.2
80
0
70
60
−0.2
50
40
−0.4
30
−0.6
20
10
−0.8
0
200
−1
100
0
160
140
120
100
80
60
40
20
(c) Original Protein Dataset
0
−1.2
−0.5
0
0.5
1
1.5
2
2.5
3
(d) Protein dataset embedded in 2D
with l=8
Figure 3.20: Cluster separation with Locally Linear Embedding
3.6.5
Comparison with Locally Linear Embedding
In this section we compare our approach with a popular embedding technique.
Locally Linear Embedding (LLE) [99] embeds the d dimensional points in the dataset
into a smaller set of dimensions d′ , such that the local geometry of each point
is retained. Formally, given a dataset D and a parameter l, LLE first expresses
each point as a linear combination of its l neighbors such that the error ǫ(W ) =
P
P
2
Xi ∈D | Xi −
Xj ∈Rl (Xi ) Wij Xj | is minimized. The matrix W assigns weights
to the l nearest neighbors (given by Rl (Xi )) for reconstructing a point Xi . Once
the W matrix is obtained by solving a constrained least squares problem, the new
′
embedding Yi (Yi ∈ Rd ) for a point Xi is obtained by minimizing the cost function
64
Φ(Y ) =
P
Yi
| Yi −
P
Yj ∈Rl (Yi )
Wij Yj |2 .
We use LLE to embed two 3D datasets (swiss-roll and proteins datasets) into 2
dimensions. The objective is to check if the clusters in the embedded 2-dimensional
space are well separated. We use the LLE implementation provided by the author
of [99]
12
. Figure 3.20 shows the original and the embedded datasets. Notice that
LLE is able to separate out three clusters out of four from the protein dataset. Two
clusters are almost merged with each other (top right corner of Figure 3.20(d)). As
for the swiss-roll dataset, LLE linearizes the points in 2D, but a clear separation
between the clusters is not obtained. One can see that neighboring clusters in the
manifold overlap. The overlapping is an artifact of the small gap between the true
clusters.
3.7
Conclusions
In this work, we made use of a very simple idea, namely, to capture arbitrary
shapes by means of convex decomposition, via the use of the highly efficient Kmeans
approach. By selecting a large enough number of seed clusters K, we are able
to capture most of the dense areas in the dataset. Next, we compute pairwise
similarities between the seed clusters to obtain a K ×K symmetric similarity matrix.
The similarity is designed to capture the extent to which the points from the two
clusters come close to each other, namely close to the d-dimensional hyperplane that
separates the two clusters. The similarity is computed rapidly by projecting all the
points in the two clusters on the line joining the two centers (which is reminiscent
of linear discriminant analysis). We bin the distances horizontally and compute a
one-dimensional histogram to approximate the closeness of the points, which in turn
gives the similarities between the clusters. We then apply a merging based approach
to obtain the final set of user-specified (natural) clusters.
Our experimental evaluation shows that this simple approach, SPARCL, is
remarkably effective in finding arbitrary shaped-based clusters in a variety of 2D
and 3D datasets. It has the same accuracy as Chameleon, a state of the art shapebased method, and at the same time it is over an order of magnitude faster, since
12
http://www.cs.toronto.edu/~roweis/lle/code.html
65
its running time is essentially linear in the number of points as well as dimensions.
SPARCL can also find clusters in the classic Swiss-roll dataset, effectively discovering
the 2D manifold via Kmeans approximations. It does make some small errors on
that dataset. In general SPARCL works well for full-space clusters, and is not
yet tuned for subspace shape-based clusters. In fact, find arbitrary shaped-based
subspace clusters is one avenue of future work for our method.
66
(a)
(b)
(c)
(d)
(e)
(f)
Figure 3.21: Cancer Dataset: (a)-(c) are the actual benign tissue images.
(d)-(f ) gives the clustering of the corresponding tissues by
SPARCL.
CHAPTER 4
Shape-based Clustering through Backbone Identification
This chapter introduces another scalable approach to clustering spatial data. This
approach is motivated by the concepts of skeletonization within the image processing
community.
In this chapter, we present a scalable clustering algorithm that aims to identify
the underlying shape of the clusters or what we refer to as the intrinsic shape of
the clusters. We also refer to the intrinsic shape as the backbone of the clusters.
The intrinsic shape of a cluster is conceptually similar to image skeletonization
in the image processing literature. Figure 4.1(a) shows and example dataset and
Figure 4.1(d) shows its intrinsic shape. The intrinsic shape of the dataset has two
benefits:
1. Removal or reduction of noise points from the dataset, and
2. Reduction in the size of the dataset
Both these effects help in reducing the computational cost and improving the quality
of the clustering. The basic idea is to recursively collapse a set of points into a single
representative point. Over a few iterations, the dataset is repeatedly summarized
until the intrinsic shape (also referred to as the backbone) of the data is identified,
as illustrated in Figure 4.1. The contributions of this chapter can be summarized
as follows:
1. We propose a new algorithm to identify the shape (skeleton) of the clusters.
This step enables easy identification of the final set of clusters.
2. Many clustering algorithms need the true number of clusters as an input to
the algorithm. Note that DBSCAN is an exception. In this work, we outline
methods that allow us to identify the true clusters in lieu of the actual number
of clusters as an input parameter.
67
68
350
300
300
250
250
200
200
150
150
100
100
50
0
0
100
200
300
400
500
600
50
700
0
100
(a) Initial Dataset
300
250
250
200
200
150
150
100
100
0
100
200
300
400
300
400
500
600
(b) After 3 Iterations
300
50
200
500
(c) After 6 Iterations
600
50
0
100
200
300
400
500
600
(d) After 8 Iterations
Figure 4.1: Initial dataset (4.1(a)); after iterations 3 and 6; and the backbone after 8 iterations (right) of the algorithm
3. The clustering algorithm can identify clusters of varying shapes, sizes and
densities.
4.1
Related Techniques
Considerable work has been done in the field of arbitrary shape clustering.
Apart from the standard clustering methods (hierarchical, density-based and spectral) that have been described in Section 2.2.2, certain alternate clustering algorithms, such as those inspired from various physical and natural phenomenon, have
69
also been proposed. More specifically, clustering algorithms motivated by concepts
from swarm intelligence [1] and biologically inspired models have been proposed recently [91]. These algorithms are characterized by individual data points that are
termed agents, that interact with and alter their local environment under defined
principles. In [35], the authors propose a flocking based spatial clustering algorithm.
Each agent within the flocking model moves under separation, cohesion and alignment behaviors modeled after the flocking phenomenon of birds. The movement of
agents under these behaviors repeated over pre-defined iterations results in clusters
of agents. Separation ensures that agents maintain certain distance from neighboring agents. Movement of agent under the cohesive behavior allows agents to form
clusters.
Another line of work inspired from physical sciences, models cluster centers
as centers of gravitational forces [121, 93, 43, 70] exerted by data points
13
on
each other. In [43], the authors determine clusters by moving points under the
Gravitational Law and Newton’s motion law. While the authors claim that the
number of clusters are determined automatically, the proposed algorithm requires a
number of other parameters (α: minimum number of points permissible in a cluster,
ǫ: clustering merging distance bound). Moreover, the clusters captured are convex
in shape. In [93], the authors compare hierarchical clustering with gravitational
clustering.
Clustering algorithms motivated by principles from magnetism have been proposed [12, 9] as well. In [12], the authors use the spin-spin correlation function to
determine clusters. Each data point is assumed to possess a Potts spin variable.
Within the Potts spin model, at super–paramagnetic temperatures spin variables
belonging to the same cluster get aligned with each other. The spin-spin correlation
function is estimated using Monte Carlo methods, which in turn governs the size
and number of clusters.
13
A data point is considered as a unit-mass particle that is exposed to gravitational forces
70
4.1.1
Skeletonization
Skeletonization (also known as thinning) from image processing literature con-
ceptually resembles the approach proposed in this chapter. Let us take a brief look
at skeletonization from the image processing perspective, although we will not make
use of image processing algorithms in this work.
Skeletonization is the process of peeling off from an image as many pixels
as possible without affecting the general shape of the image. In other words, after
pixels have been peeled off, the image should still be recognized. The skeleton hence
obtained must have the following properties. It should be 1) as thin as possible, 2)
connected, and 3) centered. Figure 4.2, shows an image and its skeleton. Skeletons
Figure 4.2: Example skeleton of a binary image (in black). The white
outline is the skeleton.
have many mathematical definitions. Some of the definitions are as follows:
1. Fire propagation model: Blum [13] described a skeleton in terms of a fire
propagation model. Assume that a region of prairie grass has the shape of
the object whose skeleton has to be determined. Assume that a fire is lighted
along each edge of the region. The points on the prairie region where two or
more “fronts” of fire meet form the skeleton of the region. Blum defined the
Medial Axis Transform (MAT) to determine the skeleton.
2. Centers of bi-tangent circles: This approach is conceptually similar to the
Medial Axis Transformation. This method considers a point p (within the
region R) to be a part of the skeleton if p is equidistant from two points on
the boundary of R.
71
3. Centers of maximal disks: If disks are placed on the region R to be skeletonized, such that the size of the disk cannot be increased without intersecting
the boundary of R, then the centers of these maximal disks define the skeleton.
Numerous algorithm for skeletonization have been proposed in the image processing
community. Morphology based techniques [44] along with iterative thinning algorithms [23] are commonly used for identifying skeletons. These algorithms rely
heavily on the binary pixel based representation of the data and on the notion of
foreground and background pixels. Morphological operators are applied on a pixel
and its neighborhood to achieve various effects (e.g. thinning, thickening, hole filling,
etc.). The strict adherence to the pixel based representation makes these methods
infeasible for our data.
4.2
The Clustering Algorithm
Our approach to clustering is motivated by the notion that a cluster possesses
an intrinsic shape or a core shape. Intuitively, for a 2-dimensional Gaussian cluster, points around the mean of the cluster could be considered as points forming
the core shape of the cluster. For an arbitrary shaped cluster, such as shown in
Figure 4.1(a), the intrinsic shape of the cluster is captured by the backbone of the
cluster (Figure 4.1(d)). The clustering algorithm has two phases. In the first phase
we identify the intrinsic shape of the clusters. In the following phase, the individual
clusters are separately identified.
4.2.1
Preliminaries
Consider a dataset D of N points in d-dimensional Euclidean space. The
distance between points i and j is represented by dij . The k-nearest neighbors (kNN) of a data point i are given by the set Rk (i). The nearest neighbors for all points
are captured in the matrix A. Each entry A(i, j) is given by

 1 if j ∈ R (i)
k
A(i, j) =
 0 if j ∈
/ Rk (i)
72
The term k-NN matrix is used for A henceforth. The entry A(i, j) can be viewed
as the probability of point j being in the k-NN set of i.
4
Figure 4.3(a) (left)
4
5
3’={4,5}
7
3
3
2
4
3
4’={6,7}
6
1’ = {1,2}
2
2
2’={3}
1
1
1
1
2
3
4
5
1
2
3
4
5
(a) Sample Dataset
Figure 4.3: Sample dataset showing one iteration of glob and movement
shows a sample dataset and Figure 4.4(a) shows the corresponding k-NN matrix.
Figure 4.3(a) (right) shows the sample dataset after one iteration, while Figure 4.8(a)
shows the corresponding updated k-NN matrix.
For the sake of clarity, the notation kn (n subscript for neighborhood) is used
to denote the k parameter in a nearest neighbor context. Whenever required, the
notation kc would imply the true number of clusters in a dataset.





A0 = 




0
1
1
0
0
0
0
1
0
1
0
0
0
0
1
1
0
0
0
0
0
0
0
0
0
1
1
0
0
0
0
1
0
0
1
0
0
0
1
0
0
1
0
0
0
0
1
1
0










(a) Initial k-NN matrix for sample data

0
 1
A1 = 
 0
0
1
0
1
1
1
1
0
1

0
0 

1 
0
(b) Updated k-NN matrix
after first iteration
Figure 4.4: k-NN matrices for sample dataset
73
4.2.2
Phase 1 – Backbone Identification
We hypothesize that, given the points in the backbone, the initial dataset can
be obtained through the following hypothetical generative process. Let us assume
that the backbone of a cluster has Nt points. Assume that each backbone point
pi has two parameters associated with it. The weight parameter for pi , denoted
by wi , indicates the number of points that can be generated from pi . The spread
parameter, indicates the region around pi within which wi points can be generated.
For a d-dimensional input space, a covariance matrix, σi could represent the spread
parameter. For the sake of simplicity, we assume that the covariance matrix is a
diagonal matrix with the same variance vi along each dimension. Now, assume
that a Gaussian process generates m (m < wi ) points at random, with mean at pi
and the covariance matrix σi dictating the distribution of these points. The weight
wi is distributed (either uniformly or as a function of the distance of the point
from pi ) across the generated m points. The covariance matrix for the m points is
obtained by updating σi such that the spread volume for the m points is decreased
in proportion to weights assigned to them. This generative process is repeated at
each new point until the weight assigned to a new point has reduced to one. A
weight wi = 1 indicates that a point cannot generate any points. We propose this
simple generative model for obtaining the original dataset from the backbone.
Contrary to the generative model, we want to identify the points belonging
to the backbone given the original dataset. In essence, our approach tries to run
the generative model in reverse. In other words, we follow a “reverse generative”
process. Notice that the backbone has much less noise as compared to the original
set of points, making it easier to identify the individual clusters. The task now is to
capture this backbone or the core shape. To identify this core backbone shape, we
propose an algorithm based on two simple concepts:
1. Globbing: Globbing involves assigning a representative to a group of points.
The globbed points are removed from the dataset and their representative
(point) is added. Each point, in the dataset, has a weight w assigned to it.
Initially, the weight of each point is set to 1. The weight of a representative
is proportional to the number of points globbed by the representative. All
74
points that lie within a d-dimensional ball of radius b, around a representative
r are globbed by r. As discussed later, the value of b is estimated from the
dataset. To illustrate the effect of globbing, Figure 4.5 shows the bubble plot
corresponding to Figure 4.1(d). Each point is replaced by a bubble wherein
the size of bubble is proportionate to the number of points globbed by it.
Figure 4.5: Bubble plot for Figure 4.1(d). The size of a bubble is
proportionate to the weight wi of a point.
2. Object Movement: In our model, each point experiences a force of attraction from its neighboring points. Under the influence of these forces a point
can change its position. The magnitude and direction of movement is proportionate to the forces exerted on the point.
find core clusters(D, k):
1. Initialize wi = 1, ∀i
2. r = estimate knn radius(D, k)
3. repeat
4. glob objects(D, r, k)
5. Dnew = move objects(D, r, k)
6. D = Dnew
7. until stopping condition satisfied
8. C = identify clusters(D)
Figure 4.6: The Backbone Identification Based Clustering Algorithm
75
The backbone identification algorithm involves two steps that are repeated iteratively. In the first step, objects are globbed starting at the most dense regions of
the dataset. In the following second step, objects move under the influence of mutual forces. Figure 4.3(a) shows the initial dataset consisting of 7 points and the
effect of one iteration (globbing followed by movement) on the dataset. Similarly,
Figures 4.4(a) and 4.8(a) show the initial k-NN matrix A0 and the updated k-NN
matrix A1 after one iteration, respectively. On convergence of the iterative process,
the intrinsic shape of the cluster is expected to emerge. Figure 4.1(d) shows the
backbone of the dataset in Figure 4.1(a), on convergence. Note that the two steps
outlined in the algorithm are essentially simulating the generative model in reverse.
The algorithm is outlined in Figure 4.6. estimate knn radius computes an estimate for the average distance to the k th nearest neighbor for objects in the dataset.
The radius is estimated by first obtaining the distance to the k th nearest neighbor
over a random sample from the original dataset. The largest 5% of these distances
are eliminated and the average radius is computed from the remaining 95%. This
average radius is used as the globbing radius r.
During glob objects all points within a radius r of a point a are marked as being
“globbed” by a. The use of the globbing radius r in the globbing step ensures that
only points in the close proximity of a can be represented by a. Such selective globbing also ensures that outlier or noise points do not glob points belonging to dense
cluster regions. Globbing modifies the dataset by removing the globbed points and
by updating the weight wa of the globbing point to include the weights of all the
P
globbed points (i.e. wa = ∀p s.t. dist(p,a)<r wp ).
In the move objects step, a point b in d-dimensional space is displaced under the
influence of its nearest neighbors’ force of attraction. Out of the k nearest neighbors,
only those that have not been globbed by b participate in displacing b. The force
exerted by an object c on object b is proportional to wc and inversely proportional
to dist(b, c), where dist() is some distance function. The updated position of b in
dimension i is given by Equation 4.1, where bi is the ith dimension of b.
bi =
b i · wb +
wb +
P
c∈Rk (b) ci
P
c∈Rk (b)
1
dist(b,c)
1
dist(b,c)
· wc ·
wc ·
(4.1)
76
r
f1
11
00
00
11
f3
a
f
2
Figure 4.7: Example illustrating the globbing-movement twin process.
Figure 4.7 elaborates the globbing and movement steps. For a point a (shown in
red) the 8 nearest neighbors are marked in blue. Out of the 8 nearest neighbors,
5 lie within radius r, as a result they are globbed by a. The remaining 3 nearest
neighbors are responsible for moving a. The forces exerted by these points on a are
shown by the vectors f1 , f2 and f3 . The resultant direction in which a moves is the
vector sum of f1 , f2 and f3 .
One can extrapolate that the above two steps repeated without a suitable
stopping condition would result in a dataset with a single point which globs all the
points in the dataset. Let Dn be the dataset after iteration n. D = D0 and let Df inal
be the dataset obtained after Line 6 of Figure 4.6. Clustering quality is poor if Df inal
has points that represent globbed points from more than one natural cluster. At the
same time, if Df inal is very similar to D0 , then we have not achieved any reduction in
the dataset size. Hence, a “good” stopping condition needs to balance the reduction
in the dataset size and the degree to which Dn captures D0 .
To formalize this notion, let An be the k-NN matrix after iteration n. The
initial k-NN matrix for the dataset is A (or A0 ). Let the size of An be Nn × Nn ,
where Nn is the number of points in the dataset at the end of iteration n. Consider
fn : Rd → Rd be an onto function for iteration n. Function fn maps a point a in the
original dataset D0 to a point in Dn that has globbed a. Given that fn (a) = fn (b),
i.e., both a and b are globbed by the same point in Dn , the probability that b is in
the k-neighborhood of a is approximated by the expression:
s(f (a))−2
Pr[b ∈ Rk (a)] =
Ck−2n
s(f (a))−1
Ck−1n
, if fn (a) = fn (b)
(4.2)
77
where s(x) is the number of points globbed within x. The above equation can be
explained as follows. The numerator corresponds to the number of sets of points
of size k − 2 (considering a and b to be included in the set) that can be selected
from s(fn (a)) − 2 points. The denominator corresponds to the number of sets (of
points) that include point a. Essentially, the probability is given by the ratio of
the two selections. In the alternate scenario, when fn (a) 6= fn (b), the probability of
b ∈ Rk (a) is given by the expression
s(f (a))+s(f (b))−2
n
Ck−2n
1
Pr[b ∈ Rk (a)] =
· s(fn (a))+s(fn (b))−1 , if fn (a) 6= fn (b)
d(fn (a), fn (b)) Ck−1
(4.3)
The probability in Equation 4.3 depends on two factors: 1) the number of points
globbed by the representatives of a and b in Dn , and 2) the distance between the
representatives fn (a) and fn (b). The larger the distance between fn (a) and fn (b),
the smaller the probability of b belonging to Rk (a). Similarly, the probability in
Equation 4.3 is less than that in Equation 4.2. This resonates with the intuition that
nearby points should have higher probability. Note that although the k-NN relation
is not symmetric, the above probabilities are symmetric, i.e., Pr[b ∈ Rk (a)] =
Pr[a ∈ Rk (b)]. Note that for the Equations 4.2 and 4.3 to represent probabilities,
P
the right hand side should be normalized by dividing by the term Za = b Pr[b ∈
Rk (a)]. Let Mi be the N0 × N0 matrix with the entry Mi [x, y] representing Pr[y ∈
Rk (x)]. Figure 4.8 shows the M1 matrix (without the normalizing factor Z) obtained
using A1 (from example in Figure 4.4) and Equations 4.2 and 4.3. For the sake of
comparison, the original k-NN matrix A0 is also shown alongside.
Given the above description, the stopping condition for Algorithm 4.6 can be
formulated in terms of the Minimum Description Length (MDL) principle.
4.2.2.1
Minimum Description Length principle
Minimum Description Length (MDL) principle [97] is a model selection criteria. The MDL principle originates from the more general theory of Occam’s razor.
Occam’s razor states that given two approaches that are equivalent in all other
respects, select the one that is simpler. By considering that the simplest represen-
78



0
1
0.5 0.083 0.083 0.066 0.066
0 1 1
 1

 1 0 1
0
0.5
0.083
0.083
0.066
0.066



 0.5 0.5

 1 1 0
0
0.16
0.16
0.083
0.083



 A0 =  0 0 0
0.083
0.083
0.16
0
1
0.33
0.33
M1 = 



0.083 0.083 0.16 1
 0 0 0
0 0.33 0.33 



0.066 0.066 0.083 0.33 0.33 0
 0 0 0
1 
0.066 0.066 0.083 0.33 0.33 1
0
0 0 0
(a) Reconstructed k-NN matrix after first iteration
0
0
0
0
1
1
0
0
0
0
1
0
0
1
0
0
0
1
0
0
1
0
0
0
0
1
1
0










(b) Initial k-NN matrix for sample data
Figure 4.8: Reconstructed (and original) k-NN matrices for sample
dataset
tation corresponds to the most compressed representation, the MDL principle takes
an information theoretic approach towards selecting a model. Let us assume that P1
is interested in transmitting the data D to P2 . Given a set of methods (hypotheses)
H used to encode the data, P1 needs to pick the hypothesis hx that has the largest
compression. For P2 to decode the data, it needs the hypothesis hx as well as the
data that is encoded using hx . Let L(hx ) be the number of bits required to represent
the hypothesis and L(D | hx ) be the encoded data given hypothesis hx . The MDL
principle suggests selecting the model that minimizes L(hx ) + L(D | hx ). One can
notice that the MDL principle balances the generality and the specificity (the biasvariance trade-off) in model selection for the data. A simple model requires fewer
number of bits corresponding to the L(hx ) term, but it results in a larger number
of bits to represent the data L(D | hx ). On the contrary, a complex model would
exhibit just the opposite effect. The term L(D | hx ) also corresponds to the error
introduced in the transmission as a result of selecting the model hx .
In the context of our clustering algorithm, the set of hypotheses/models is
represented by Di , ∀i > 0. The simplest model D1 requires the largest number
of bits, but requires fewest number of bits to encode D. Stated another way, the
simplest model has the smallest error when it comes to reconstruction of the original
data. This is often called as the reconstruction error. For subsequent hypotheses,
as L(Di ) decreases, the additional data required to represent D0 (given by L(D0 |
Di ), i > 0) increases. L(D0 | Di ) can be interpreted as the error introduced in
reconstructing D0 from Di .
79
Representing the model and the data: As seen before, Ai represents the k-NN
matrix for Di . Let Mi represent the k-NN matrix “reconstructed” from Ai using
Equations 4.2 and 4.3. The probability that the reconstructed k-NN matrix Mi
faithfully captures A0 is given by Pr[A0 | Mi ]. Since each element in A0 can be
considered independent, Pr[A0 | Mi ] can be expressed as
Pr[A0 | Mi ] =
N0 Y
N0
Y
Pr[A0 (m, n) | Mi (m, n)]
(4.4)
m=0 n=0
Since A0 is a binary matrix, as a result the expression Pr[A0 (m, n) | Mi (m, n)] is
given by
Pr[A0 (m, n) | Mi (m, n)] =



Mi (m,n)
if A0 (m, n) = 1
1−Mi (m,n)
if A0 (m, n) = 0
(4.5)
The number of bits required to represent the total reconstruction error is captured
by
L(D0 | Di ) = − log Pr[A0 | Mi ]
N0 X
N0
X
= −
log Pr[A0 (m, n) | Mi (m, n)]
(4.6)
m=1 n=1
The number of bits to represent the model depends on the relative size of Di . It is
given by the following expression
L(Di ) = − log(
| Di |
)
| D0 |
(4.7)
Hence the trade-off at the end of any iteration i is between the average reconstruction
error given by
1
L(D0
N02
| Di ) and the size of the model L(Di ). The term L(D0 | Di )
normalized by divided with N 2 , gives the average number of bits per entry in the
matrix. Computing the reconstruction matrix is O(N 2 ) for each iteration, where N
is the number of points in the original dataset. As a result, this is not a feasible
approach to ascertain the stopping condition. We present a stopping condition that
is simpler to compute but captures the same trade-off between the reconstruction
error and the dataset size.
80
A Practical Stopping Condition: Since the above stopping condition is computationally expensive, we provide a practical stopping condition that can intuitively
shown to be related to the MDL based formulation stated above.
In a dataset, if points are only globbed (without moving), it results in the
sparsification (reduction) of the data. In addition, moving points enables further
globbing in subsequent iterations. In other words, if gi is the number of points
globbed in an iteration and mi is the number of points that are moved in an iteration,
gi ∝ mi−1 . This is shown in Figure 4.9.
Number of points
120000
No. points moved
No. points globbed
100000
80000
60000
40000
20000
0
2
3
4
5
6
7
Iterations
8
9
10
Figure 4.9: The number of points moved and globbed per iteration for a
dataset with 1000K points.
Intuitively, as more points are globbed across the iterations, the reconstruction error
increases. Let Ei be the reconstruction error at the end of iteration i and let the
error difference between two consecutive iterations be ∆Ei (∆Ei = Ei − Ei−1 ).
The difference between the errors is proportional to the number of points globbed,
i.e., ∆Ei ∝ gi . Combining this with the previous observation (gi ∝ mi−1 ) yields
∆Ei ∝ mi−1 .
As fewer points move in subsequent iterations (mi < mi−1 ), it reflects the decline
in the size of the dataset, i.e., Ni < Ni+1 . The ratio
mi
(<
mi−1
1) captures the relative
rate of this decline.
To state upfront, if the expression
mj−1
mj
<
mj−2
mj−1
(4.8)
81
does not hold then the iterative process is halted, else continued. The above discussion helps understand this stopping condition. Let us look at Figure 4.10 showing
the two contradicting influences – dataset size and reconstruction error – in an MDL
based formulation of our clustering problem. Although the ratio
mj
mj−1
is less than
1
Reconstruction Error
Relative Dataset size
0
Iterations
Figure 4.10: Balancing the two contradicting influences in the clustering
formulation.
one, the condition in Equation 4.8 is encouraging an increase in this ratio. It implies
that the stopping condition encourages a rapid decrease in the size of the dataset,
by the relation mi ∝ Ni . The downward sloping arrow along the ‘Reconstruction
Error’ curve in Figure 4.10 represents this effect. Moreover, as mi is less than mi+1 ,
i+1
∆Ei+1 is less than ∆Ei . The relative error difference ( ∆E
) is increasing as long
∆Ei
as the condition in Equation 4.8 is satisfied, as a result of mi being less than mi−1 .
Hence, the condition in Equation 4.8, does not favor a decline in the relative error
difference. In the context of Figure 4.10, this is depicted by the downward sloping
arrow along the ‘Reconstruction Error’ curve. At the iteration at which the stopping condition in Equation 4.8 is violated, both the above effects (increasing relative
reconstruction error and the rate at which the dataset size is decreasing) are not
satisfied. We chose to stop at this iteration. Intuitively, this is indicated by the
intersection point of the two curves in Figure 4.10.
At the end of the iterative process a much smaller dataset Dt , as compared to the
original dataset, is obtained. This dataset preserves the structural shape of the
original dataset.
82
4.2.3
Phase 2 – Cluster Identification
Once the intrinsic shape of the clusters is identified, the task remains to isolate
the individual clusters. The first phase (Section 4.2.2) helps drastically reduce the
noise while reducing the size of the dataset considerably.
Let us consider two cases within cluster identification. First case deals with
the possibility that the desired number of clusters is pre-specified. In the second
case, the algorithm needs to determine the number of clusters automatically.
Number of clusters c specified: In this scenario, obtaining the clusters is fairly
straight forward. Since the original dataset is significantly reduced in size after the
first phase, any computationally inexpensive clustering algorithm can be applied
to Dn . We show results of applying hierarchical clustering (CHAMELEON) in
Section 4.3.
Number of clusters unspecified: When the number of clusters are not specified,
the identify clusters(D) method in Figure 4.6 proceeds in two stages. In the
first stage, running a connected components algorithm on Dt delivers the set of
preliminary clusters C. In the second stage, the clusters in C are merged to obtain
the final set of clusters.The merging process is based on a similarity metric. For
each pair of clusters in C two similarity measures are defined. Let B(Ci , Cj ) be the
points in cluster Ci that have a point from Cj in their k-NN set, i.e. B(Ci , Cj ) =
pi ∈ Ci | ∃pj ∈ Rk (pi ) ∧ pj ∈ Cj . We call B(Ci , Cj ) the border points in cluster Ci
to cluster Cj . Note that B(Ci , Cj ) need not be the same as B(Cj , Ci ). Let E(Ci , Cj )
be the total number of occurrences of points in Cj in the k-neighborhood of points
P
in Ci , i.e., E(Ci , Cj ) = pi ∈Ci | pj | pj ∈ Rk (pi ) ∧ pj ∈ Cj |. Let B(Ci ) be the set
S
of all border points in cluster Ci , i.e., B(Ci ) = ∀Cj 6=Ci B(Ci , Cj ) The first similarity
metric S1 is given
S1 (Ci , Cj ) =
| E(Ci , Cj ) |
>α
| B(Ci , Cj ) |
(4.9)
The higher the value of the ratio in Equation 4.9, the greater the similarity between
the clusters. A high value for S1 (Ci , Cj ) indicates that the points in Cj are close
to the border points in Ci . This similarity metric captures the degree of closeness,
measured in terms of local neighborhood of border points, between a cluster pair.
83
The second similarity measure we define, S2 , is given by
S2 (Ci , Cj ) =
| B(Ci , Cj ) |
>β
| B(Ci ) |
(4.10)
The similarity S2 (., .) ensure that two clusters can be merged only if the interaction
“face” (fraction of border points) between the two clusters is above the β threshold.
Cluster pairs are iteratively merged, starting with the pair with highest similarity.
For two clusters Ci and Cj to be merged both conditions in Equations 4.9 and 4.10
must be satisfied. Since the true number of clusters are not specified, we need
to provide lower-bound thresholds (α and β) for the similarity criteria to continue
merging of clusters.
4.2.4
Complexity Analysis
Let us assume that the above algorithm converges after t iterations. The
number of points at the end of each iteration is given by N0 , N1 , ..., Nt . For each point
p (in each iteration i) that globs its nearest neighbors, a k-NN search is performed on
1− d1
the dataset. Since we use a kd-Tree to store the points, a k-NN search takes O(Ni
)
time complexity. Let G1 , G2 , ..., Gt be the number of points that have globbed other
points, in each of the iteration. The total complexity of the k-NN searches is given
P
1− 1
by O( ti=1 Gi · Ni d ). Moving the points involves computing the new location
based on the k-NN. If M1 , M2 , ..., Mt represents the number of points that move in
P
each iteration, the total cost of moving across all iterations is given O(k · ti=1 Mi ).
When CHAMELEON is applied to the set of points after the iterative process, the
computational cost is O(Nt log Nt ). Hence the total computational cost is the sum
of the above terms. Let us assume that a constant fraction of points are globbed
and moved in each iteration, i.e., Gi = Mi = O(1). Also let us assume that in the
worst case the number of points in each iteration are O(N0 ), i.e., Ni = O(N0 ). In
the worst case, the runtime complexity of the algorithm is O(tN0 +kN0 +N0 log N0 ),
where t is the number of iterations of the algorithms and k is the number of nearest
neighbors selected.
84
4.3
Experimental Evaluation
In this section we will briefly look at the performance results for the above al-
gorithm. We only cover the scenario where the true number of clusters are specified.
4.3.1
Datasets
The same datasets that were used for SPARCL in Chapter 3 are used here.
Broadly, a set of synthetic datasets containing 13 clusters of arbitrary shapes are
used for the scalability experiments. Some of the commonly used datasets in the
literature have also been explored. The experiments are conducted on a Mac G5
machine with a 2.66 GHz processor, running the Mac 10.4 OS X. Our code is written
in C++ using the Approximate Nearest Neighbor Library (ANN)
4.3.2
14
.
Scalability Results
To study the scalability of the proposed algorithm, we generate synthetic
datasets of varying number of points. The number of noise points are set constant at 5% of the total dataset size. The dimensionality of the dataset is d = 2
and the number of clusters are fixed at 13. For each dataset k is set at 70. The first
column in Table 4.1 specifies the size of the datasets, the largest being a dataset
with 1 million points. The table breaks down the total execution time into the time
taken during the iterative process (Column 2) and the CHAMELEON execution
time on the final dataset after the iterative steps (Column 4). The number of iterations performed and the size of the final dataset (as a percentage of the initial
dataset) after t iterations are shown in Columns 3 and 5, respectively. Execution
time results for 3D datasets (protein and swiss roll) have also been shown in this
table. As observed from the table, the time taken by the iterative process increases
with the increasing size of the dataset. Also, different datasets exhibit varying degrees of dataset reduction. The time taken by CHAMELEON is proportional to
the dataset reduction achieved. This is evident from the observation that the time
taken by CHAMELEON on the 1000K dataset is ten times less than that for the
800K dataset. The reduction in the dataset is purely a factor of the density of the
14
http://www.cs.umd.edu/~mount/ANN/
85
points and also the relative position of the points. As such, no concrete reasoning
for better reduction with the 1000K dataset can be tendered.
1600
SPARCL(random)
Backbone-based clustering
1400
Time (sec)
1200
1000
800
600
400
200
0
0
100
200
300
400
500
600
# of points x 1000 (d=2)
700
800
900
1000
Figure 4.11: Scalability Results for Backbone Based Clustering
Figure 4.11 compares the execution time taken by random seeded SPARCL with
the method proposed in this chapter. The time reported is the total execution
time, i.e., time for iterative steps and time taken by CHAMELEON. To remind
the reader, randomly seeded SPARCL is faster as compared to SPARCL that is
seeded using the LOF technique. Moreover, both forms of SPARCL are an order of magnitude faster as compared to contemporary clustering algorithms. As a
result, those comparison have been omitted here. To summarize, the backbone
based clustering approach is around an order of magnitude faster as compared
to SPARCLṠince SPARCL itself is an order of magnitude faster than contemporary
clustering algorithms (CHAMELEON and DBSCAN), the backbone based approach
is two orders of magnitude faster than CHAMELEON and DBSCAN. Figure 4.12
shows the “skeletons” or reduced datasets for some of the common datasets in the
literature (Fig. 4.12(b) and 4.12(d)). The skeletons for 3D datasets (protein and
swiss roll) are also shown in Figure 4.13. For the sake of comparison, the number
of points in each dataset are also show. The 3D datasets exhibit a predominant
86
Dataset
(no. of
points)
10K
50K
100K
200K
400K
600K
800K
1000K
protein
(14669)
swiss roll
(19386)
Time for t Number of
Time for
Dataset size
iterations iterations CHAMELEON on
after t
(sec)
(t)
dataset post t
iterations (% of
iterations (sec)
initial size)
0.503
4
0.428
4.41%
3.00
4
1.08
4.07%
5.597
4
1.616
5.2%
12.159
4
7.66
5.98%
26.467
4
25.130
6.94%
40.923
4
58.732
6.88%
57.503
4
109.935
7.49%
113.861
10
10.501
1.78%
1.119
5
1.068
13.8%
1.38
6
1.16
12.74%
Table 4.1: Scalability results on dataset with 13 true clusters. The size
of the dataset is varied keeping the noise at 5% of the dataset
size.
sparsification effect as compared to a skeletonization effect.
4.3.3
Clustering Quality Results
As in Chapter 3, an external criterion, namely purity score is used to measure
the clustering quality. Recall that the purity score lies in the range [0, 1]. Like
before, the noise points are eliminated while computing the purity, since different
algorithms deal with noise points differently. Figure 4.14 shows the purity score for
the synthetic datasets used earlier. The purity is fairly stable apart from the score
for dataset of size 600K. As compared to SPARCL the purity score of the proposed
method is less by a small fraction. This is because the globbing and movement
process at times tends to glob border points with noise points.
4.3.4
Parameter Sensitivity Results
We performed experiments to test the sensitivity of the algorithm to the input
parameter k (number of nearest neighbors). For a given dataset, we alter k and
record the clustering quality. We selected the dataset with 800K points for this
87
350
300
300
250
250
200
200
150
150
100
100
50
0
0
100
200
300
400
500
600
700
50
0
100
(a) 8000 points
200
300
400
500
600
(b) 1077 points
500
450
450
400
400
350
350
300
300
250
250
200
200
150
150
100
100
50
0
0
100
200
300
400
500
600
700
50
0
100
(c) 1000 points
200
300
400
500
600
700
(d) 838 points
Figure 4.12: Backbone/skeleton of 2D synthetic datasets in our study.
Left column: original dataset, right column: skeletons.
experiment. Figures 4.15(a) and 4.15(b) show the run time and purity,respectively,
as the value of k is varied. Figure 4.15 shows the execution time and purity as
the number of nearest neighbors are increased. Note that the purity score remains
almost the same. From Figure 4.15(a) one can see that the execution time increases
linearly as the k parameter is gradually increased.
4.4
Conclusion
In this chapter, we proposed another method for clustering large spatial point
datasets. Like SPARCL this method too results in a reduced dataset, which we call
as the backbone of the original dataset. Finding clusters in the backbone amounts
to identifying clusters in the original dataset. The algorithm performs two steps
88
60
50
40
20
0
0
15
15
10
10
15
5
5
15
10
0
0
10
5
−5
5
−5
0
0
−5
−10
−10
−5
−10
−15
−15
−15
(a) 19386 points
−10
(b) 2471 points
90
90
80
80
70
70
60
60
50
50
40
40
30
30
20
20
10
10
0
0
150
200
100
100
50
0
160
140
120
100
80
60
40
20
0
(c) 14669 points
0
150
100
50
0
(d) 2023 points
Figure 4.13: Backbone/skeleton of 3D synthetic datasets in our study.
Left column: original dataset, right column: skeletons.
(globbing and movement) iteratively, resulting in a substantially reduced dataset
that still captures the structural shape of the clusters. From the experimental
evaluation we see that the algorithm is more scalable as compared to SPARCL.
4.4.1
Comparison with SPARCL
Since both SPARCL and the proposed approach target the space of scalable
clustering algorithms, they have considerable similarities and some subtle differences. Following are some notes comparing the two.
1. In its first stage, SPARCL aims to identify representatives from the entire
dataset that would capture the dense regions (clusters) in the dataset. On
the other hand, the current method tries to retain the structure in the data,
89
Purity score
1
0.8
0.6
0.4
0.2
Backbone-based clustering
SPARCL(lof)
0
0 100 200 300 400 500 600 700 800 900 1000
Dataset Size (x 1000)
2000
1800
1600
1400
1200
1000
800
600
400
200
1.1
1
Purity score
Time (sec)
Figure 4.14: Purity score with varying dataset size
0.9
0.8
0.7
0.6
Time
0
50
100 150 200 250 300 350 400
k nearest neighbors
(a) Execution time
Purity score
0.5
0
50
100 150 200 250 300 350 400
k nearest neighbors
(b) Purity score
Figure 4.15: Execution time and purity for varying number of nearest
neighbors
while globbing and moving the points. In some sense, the backbone is the
representative for the entire dataset.
2. SPARCL takes a projective approach, wherein the points belonging to the two
clusters are projected onto the line connecting their centers. As the dimen-
90
sionality of the data is increased, this approach is likely to result in misleading
similarity scores. This is because even points that are far apart can get project
onto the same bin, resulting in a misleading score. The backbone based approach on the other hand, can suffer from the curse of dimensionality as it
relies extensively on nearest neighbor queries.
3. Although SPARCL has superior run time complexity, in practice the backbone
based clustering algorithm turns out to be more efficient.
4. In some sense SPARCL is a parametric approach since it assumes that regular
isotropic clusters can be overlayed on the true clusters. The current algorithm
is non-parametric that way, since it does not make any assumptions and infers
any information directly from the data.
CHAPTER 5
Conclusion and Future Work
Chapters 3 and 4 cover our existing contributions on shape-based clustering. This
chapter covers some future directions in shape-based clustering.
5.1
Efficient Subspace Clustering
4
3
4
2
3
2
1
0
Z axis
Z axis
1
−1
0
−1
−2
−2
−3
−3
−0.5
−4
−0.42 −0.44 −0.46 −0.48 −0.5 −0.52 −0.54 −0.56 −0.58 −0.6
−1 0
Y axis
−4
1
−1
X axis
−0.4
−0.5
0
0.5
1
Y axis
X axis
(a) View perpendicular to the YZ plane
(b) View perpendicular to the XZ plane
Figure 5.1: Subspace clustering – Challenges for SPARCL
As a future direction, we are interested in exploring the possibility of extending SPARCL and the backbone method to subspace based clustering. Subspace
clustering is useful for applications where the patterns/clusters lie within a smaller
set of dimensions.
As noted earlier our current solutions are designed for full-space clustering, i.e., the
clusters are assumed to span all the dimensions. Preliminary experiments show, for
example, that SPARCL cannot detect subspace clusters effectively. This is because
a subspace cluster can have very sparsely distributed points in dimensions other
than the subspace dimensions. As a result, the similarity score between the seed
clusters computed by SPARCL will end up being small, indicating separate clusters.
This is illustrated in Figure 5.1. Consider a cluster in XZ subspace, as shown in
91
92
Figure 5.1(b). The same cluster appears as a sparse set of points when viewed along
the direction perpendicular to the Y Z plane. If a projection based approach is taken
(as in SPARCL), the seed clusters are likely to end up having very small scores for
inter-cluster similarity, due to the sparsity of the data. The subspace criterion of
the seed clusters is not taken into account in the similarity computation. As a result, the similarity between two clusters in different subspaces can be close to the
similarity between two clusters in the same subspace. Different approaches can be
tried for identifying the subspace clusters. Preliminary ideas regarding some of the
approaches are outlined as follows:
1. A new unified similarity metric needs to be defined that takes into account
the dimensionality of the seed clusters along with the distance similarity. Currently, in SPARCL, the similarity S(X, Y ) is a function of the distance and
density of the two pseudo-clusters. This similarity should also include the
dimension compatibility between the two pseudo-clusters X and Y .
2. A projective approach such as taken by [2] can be combined with SPARCL.
Using the concepts in [2], a large number of convex polytopes in different
subspaces can be determined. The convex polytopes can now be merged to
obtain the final set of clusters. In this method too, the SPARCL similarity
metric has to be a function of the dimensions involved.
5.2
Shape Indexing
Considerable work on indexing and matching shapes has been done [123, 120].
Some of the work from the data mining community in this area has focused on
converting the shapes to a time series and then indexing the time series [67]. The
drawback of such time series based methods is that they only consider the boundary
of the shape, independent of other factors such as the density of points within
the shape. Our idea is based on the Local Outlier Factor proposed in Chapter 3.
Although, never explicitly stated, the representatives selected by the LOF approach
are rotation invariant as shown in Figure 5.2. Which also means that the distances
to k-nearest neighbors from each point are preserved. This fact can be used to index
93
250
-300
11
6
12
-320
7
200
7
11
2
4
9
-340
9
12
5
150
-360
6
1
8
-380
8
2
4
100
-400
10
1
3
5
10
3
-420
50
420
440
460
480
500
520
540
560
580
300
(a)
350
400
450
500
(b)
Figure 5.2: Local Outlier Factor based representatives are rotation invariant.
shapes. From the set of selected seeds, the distance from each seed to its k-nearest
neighbors constitutes a feature vector. Let A be such a feature vector for a shape
a and let B be the feature vector for a shape b. If the shapes a and b are similar,
then A = αB, where α is the scaling factor.
Other directions: Other areas of future exploration include scaling proposed algorithms to higher dimensions using methods such as LSH and algorithms for efficient
nearest neighbor search in high dimension [112, 76].
New spatial clustering algorithm based on concepts from graph theory is another
potential direction. Graph sparsification methods can be used to sparsify the kNN
graph for the data points. Efficient sparsification methods have been proposed
in [108]. From the sparse kNN graph identifying the clusters should be an easier
task.
BIBLIOGRAPHY
[1] Ajith Abraham, Swagatam Das, and Sandip Roy. Swarm intelligence algorithms for data clustering. In Soft Computing for Knowledge Discovery and
Data Mining, pages 279–313. 2008.
[2] Pankaj K. Agarwal and Nabil H. Mustafa. k-means projective clustering. In
PODS ’04: Proceedings of the twenty-third ACM SIGMOD-SIGACT-SIGART
symposium on Principles of database systems, pages 155–165, New York, NY,
USA, 2004. ACM.
[3] Rakesh Agrawal, Johannes Gehrke, Dimitrios Gunopulos, and Prabhakar
Raghavan. Automatic subspace clustering of high dimensional data for data
mining applications. SIGMOD Record, 27(2):94–105, 1998.
[4] Alexandr Andoni and Piotr Indyk. Near-optimal hashing algorithms for approximate nearest neighbor in high dimensions. Commun. ACM, 51(1):117–
122, 2008.
[5] Anooshiravan Ansari, Assadollah Noorzad, and Hamid Zafarani. Clustering
analysis of the seismic catalog of Iran. Comput. Geosci., 35(3):475–486, 2009.
[6] D. Arthur and S. Vassilvitskii. k-means++: The advantages of careful seeding.
In Proc. of Symposium of Discrete Analysis, 2005.
[7] M. M. Astrahan. Speech analysis by clustering, or the hyperphoneme method.
Technical report, Stanford A.I. Project Memo, Stanford University, 1970.
[8] G. H. Ball and D. J. Hall. Promenade– an online pattern recognition system.
Technical report, Stanford Research Institute, Stanford University, 1967.
[9] Mats Bengtsson and Johan Schubert. Dempster-shafer clustering using potts
spin mean field theory. Soft Computing, 5(3):215–228, 2001.
[10] James C. Bezdek. Pattern Recognition with Fuzzy Objective Function Algorithms. Kluwer Academic Publishers, Norwell, MA, USA, 1981.
[11] Wu bin and Shi Zhongzhi. A clustering algorithm based on swarm intelligence.
volume 3, pages 58–66 vol.3, 2001.
[12] Marcelo Blatt, Shai Wiseman, and Eytan Domany. Clustering data through
an analogy to the potts model. In Advances in Neural Information Processing
Systems 8, pages 416–422. MIT Press, 1996.
[13] Harry Blum. A transformation for extracting new descriptors of shape. Models
for the Perception of Speech and Visual Form, pages 362–380, 1967.
94
95
[14] P. S. Bradley and U. M. Fayyad. Refining initial points for k-means clustering.
In Fifteenth Intl. Conf. on Machine Learning, pages 91–99, 1998.
[15] M. M. Breunig, H. Kriegel, R. T. Ng, and J. Sander. Lof: Identifying densitybased local outliers. In ACM SIGMOD 2000 Int. Conf. On Management of
Data, 2000.
[16] Deng Cai, Xiaofei He, Zhiwei Li, Wei-Ying Ma, and Ji-Rong Wen. Hierarchical clustering of www image search results using visual, textual and link
information. In MULTIMEDIA ’04: Proceedings of the 12th annual ACM international conference on Multimedia, pages 952–959, New York, NY, USA,
2004. ACM.
[17] Man-chung Chan, Yuen-Mei Li, and Chi-Cheong Wong. Web-based cluster
analysis system for china and hong kong’s stock market. In IDEAL ’00:
Proceedings of the Second International Conference on Intelligent Data Engineering and Automated Learning, Data Mining, Financial Engineering, and
Intelligent Agents, pages 545–550, London, UK, 2000. Springer-Verlag.
[18] V. Chaoji, M. Al Hasan, S. Salem, and M.J. Zaki. Sparcl: Efficient and
effective shape-based clustering. In Data Mining, 2008. ICDM ’08. Eighth
IEEE International Conference on, pages 93–102, Dec. 2008.
[19] B. Chazelle and L. Palios. Algebraic Geometry and its Applications. SpringerVerlag, 1994.
[20] Tom Chiu, DongPing Fang, John Chen, Yao Wang, and Christopher Jeris.
A robust and scalable clustering algorithm for mixed type attributes in large
database environment. In KDD ’01: Proceedings of the seventh ACM SIGKDD
international conference on Knowledge discovery and data mining, pages 263–
268, New York, NY, USA, 2001. ACM.
[21] Cheng T. Chu, Sang K. Kim, Yi A. Lin, Yuanyuan Yu, Gary R. Bradski,
Andrew Y. Ng, and Kunle Olukotun. Map-reduce for machine learning on
multicore. In Bernhard Schölkopf, John C. Platt, and Thomas Hoffman, editors, Advances in Neural Information Processing Systems 19, pages 281–288.
MIT Press, 2006.
[22] T. H. Cormen, C. E. Leiserson, R. L. Rivest, and C. Stein. Introduction to
Algorithms. McGraw-Hill, 2nd edition, 2005.
[23] M. Couprie. Note on fifteen 2d parallel thinning algorithms. Technical report,
Universit de Marne-laValle, IGM2006-01, 2006.
[24] Glendon Cross and Wayne Thompson. Understanding your customer: Segmentation techniques for gaining customer insight and predicting risk in the
telecom industry. SAS Global Forum, 2008.
96
[25] Xiaohui Cui, Jinzhu Gao, and Thomas E. Potok. A flocking based algorithm
for document clustering analysis. J. Syst. Archit., 52(8):505–515, 2006.
[26] Ian Davidson and S. S. Ravi. Clustering with constraints: Feasibility issues
and the k-means algorithm. In SIAM Data Mining Conference, 2005.
[27] Marcilio de Souto, Ivan Costa, Daniel de Araujo, Teresa Ludermir, and
Alexander Schliep. Clustering cancer gene expression data: a comparative
study. BMC Bioinformatics, 9(1):497, 2008.
[28] A. P. Dempster, N. M. Laird, and D. B. Rubin. Maximum likelihood from
incomplete data via the em algorithm. Journal of the Royal Statistical Society.
Series B (Methodological), 39(1):1–38, 1977.
[29] I. S. Dhillon, Y. Guan, and B. Julis. Kernel k-means, spectral clustering
and normalized cuts. In KDD ’04: Proceedings of the tenth ACM SIGKDD
international conference on Knowledge discovery and data mining, 2004.
[30] Sara Dolniar and Friedrich Leisch. Behavioral market segmentation of binary
guest survey data with bagged clustering. In ICANN ’01: Proceedings of
the International Conference on Artificial Neural Networks, pages 111–118,
London, UK, 2001. Springer-Verlag.
[31] Carlotta Domeniconi and Dimitrios Gunopulos. An efficient density-based approach for data mining tasks. Knowledge and Information Systems, 6(6):750–
770, 2004.
[32] Richard O. Duda, Peter E. Hart, and David G. Stork. Pattern Classification
(2nd Edition). Wiley-Interscience, 2000.
[33] A. J. Enright, S. Van Dongen, and C. A. Ouzounis. An efficient algorithm for
large-scale detection of protein families. Nucleic Acids Res, 30(7):1575–1584,
2002.
[34] Martin Ester, Hans-Peter Kriegel, Jorg Sander, and Xiaowei Xu. A densitybased algorithm for discovering clusters in large spatial databases with noise.
In ACM SIGKDD Int’l Conf. on Knowledge Discovery and Data Mining, pages
226–231, 1996.
[35] Gianluigi Folino and Giandomenico Spezzano. An adaptive flocking algorithm
for spatial clustering. In PPSN VII: Proceedings of the 7th International Conference on Parallel Problem Solving from Nature, pages 924–933, London, UK,
2002. Springer-Verlag.
[36] E. W. FORGY. Cluster analysis of multivariate data: efficiency vs interpretability of classifications. Biometrics, 21:768–769, 1965.
97
[37] Brendan J. Frey and Delbert Dueck. Clustering by passing messages between
data points. Science, 315:972–976, 2007.
[38] Venkatesh Ganti, Johannes Gehrke, and Raghu Ramakrishnan. CACTUS clustering categorical data using summaries. In KDD ’99: Proceedings of the
fifth ACM SIGKDD international conference on Knowledge discovery and data
mining, pages 73–83, 1999.
[39] Byron J. Gao, Martin Ester, Jin-Yi Cai, Oliver Schulte, and Hui Xiong. The
minimum consistent subset cover problem and its applications in data mining.
In KDD ’07: Proceedings of the 13th ACM SIGKDD international conference
on Knowledge discovery and data mining, pages 310–319, New York, NY, USA,
2007. ACM.
[40] J. A. Garcı́a, J. Fdez-Valdivia, F. J. Cortijo, and R. Molina. A dynamic
approach for clustering data. Signal Process., 44(2):181–196, 1995.
[41] Martin Gavrilov, Dragomir Anguelov, Piotr Indyk, and Rajeev Motwani. Mining the stock market (extended abstract): which measure is best? In KDD ’00:
Proceedings of the sixth ACM SIGKDD international conference on Knowledge
discovery and data mining, pages 487–496, New York, NY, USA, 2000. ACM.
[42] Soheil Ghiasi, Ankur Srivastava, Xiaojian Yang, and Majid Sarrafzadeh. Optimal energy aware clustering in sensor networks. Sensors, 2(7):258–269, 2002.
[43] Jonatan Gomez, Dipankar Dasgupta, and Olfa Nasraoui. A new gravitational
clustering algorithm. In In Proc. of the SIAM Int. Conf. on Data Mining
(SDM), 2003.
[44] Rafael C. Gonzalez and Richard E. Woods. Digital Image Processing (3rd
Edition). Prentice-Hall, Inc., Upper Saddle River, NJ, USA, 2006.
[45] Sudipto Guha, Rajeev Rastogi, and Kyuseok Shim. CURE: an efficient clustering algorithm for large databases. In ACM SIGMOD International Conference
on Management of Data, pages 73–84, 1998.
[46] Sudipto Guha, Rajeev Rastogi, and Kyuseok Shim. ROCK: A robust clustering algorithm for categorical attributes. In ICDE ’99: Proceedings of the 15th
International Conference on Data Engineering, page 512, Washington, DC,
USA, 1999. IEEE Computer Society.
[47] J. Han, M. Kamber, and A. K. H. Tung. Spatial Clustering Methods in Data
Mining: A Survey. Taylor and Francis, 2001.
[48] David Harel and Yehuda Koren. Clustering spatial data using random walks.
In KDD ’01: Proceedings of the seventh ACM SIGKDD international conference on Knowledge discovery and data mining, pages 281–286, New York, NY,
USA, 2001. ACM.
98
[49] William W. Hargrove and Forrest M. Hoffman. Using multivariate clustering
to characterize ecoregion borders. Computing in Science and Engg., 1(4):18–
25, 1999.
[50] Mohammad Al Hasan, Vineet Chaoji, Saeed Salem, and Mohammed J. Zaki.
Robust partitional clustering by outlier and density insensitive seeding. Pattern Recogn. Lett., 30(11):994–1002, 2009.
[51] Constantinos S. Hilas and Paris As. Mastorocostas. An application of supervised and unsupervised learning approaches to telecommunications fraud
detection. Know.-Based Syst., 21(7):721–726, 2008.
[52] A. Hinneburg and D.A Keim. An efficient approach to clustering in multimedia
databases with noise. In 4th Int’l Conf. on Knowledge Discovery and Data
Mining, 1999.
[53] Alexander Hinneburg and Hans-Henning Gabriel. Denclue 2.0: Fast clustering
based on kernel density estimation. In International Symposium on Intelligent
Data Analysis, 2007.
[54] Alexander Hinneburg and Daniel A. Keim. A general approach to clustering
in large databases with noise. Knowledge and Information Systems, 5(4):387–
415, 2003.
[55] Xiaohua Hu and Yi Pan. Knowledge Discovery in Bioinformatics: Techniques,
Methods, and Applications (Wiley Series in Bioinformatics). John Wiley &
Sons, Inc., New York, NY, USA, 2007.
[56] Woochang Hwang, Young-Rae Cho, Aidong Zhang, and Murali Ramanathan.
A novel functional module detection algorithm for protein-protein interaction
network. Algorithms for Molecular Biology, 1, 2006.
[57] C. C.J. Kuo I. Katsavounidis and Z. Zhen. A new initialization technique for
generalized lloyd iteration. In IEEE Signal Processing Letter, volume 1, pages
144–146, 1994.
[58] M. Indulska and M. E. Orlowska. Gravity based spatial clustering. In GIS
’02: Proceedings of the 10th ACM international symposium on Advances in
geographic information systems, pages 125–130, New York, NY, USA, 2002.
ACM.
[59] Anil K. Jain and Richard C. Dubes. Algorithms for Clustering Data. PrenticeHall, Inc., Upper Saddle River, NJ, USA, 1988.
[60] Woncheol Jang and Martin Hendry. Cluster analysis of massive datasets in
astronomy. Statistics and Computing, 17(3):253–262, 2007.
99
[61] Eshref Januzaj, Hans-Peter Kriegel, and Martin Pfeifle. Towards effective and
efficient distributed clustering. In In Workshop on Clustering Large Data Sets
(ICDM), pages 49–58, 2003.
[62] Klaus Julisch. Clustering intrusion detection alarms to support root cause
analysis. ACM Transactions on Information and System Security, 6(4):443–
471, 2003.
[63] Konstantinos Kalpakis, Dhiral Gada, and Vasundhara Puttagunta. Distance
measures for effective clustering of arima time-series. In ICDM ’01: Proceedings of the 2001 IEEE International Conference on Data Mining, pages
273–280, Washington, DC, USA, 2001. IEEE Computer Society.
[64] George Karypis, Eui-Hong (Sam) Han, and Vipin Kumar. Chameleon: Hierarchical clustering using dynamic modeling. IEEE Computer, 32(8):68–75,
1999.
[65] L. Kaufman and P. J. Rousseeuw. Finding groups in data. an introduction to
cluster analysis. Wiley Series in Probability and Mathematical Statistics. Applied Probability and Statistics, New York: Wiley, 1990, 1990.
[66] Eamonn Keogh. Exact indexing of dynamic time warping. In VLDB ’02:
Proceedings of the 28th international conference on Very Large Data Bases,
pages 406–417. VLDB Endowment, 2002.
[67] Eamonn Keogh, Li Wei, Xiaopeng Xi, Sang-Hee Lee, and Michail Vlachos.
Lb keogh supports exact indexing of shapes under rotation invariance with
arbitrary representations and distance measures. In VLDB ’06: Proceedings
of the 32nd international conference on Very large data bases, pages 882–893.
VLDB Endowment, 2006.
[68] Hisashi Koga, Tetsuo Ishibashi, and Toshinori Watanabe. Fast agglomerative
hierarchical clustering algorithm using locality-sensitive hashing. Knowledge
and Information Systems, 12(1):25–53, 2007.
[69] Martin Kulldorff and N. Nagarwalla. Spatial Disease Clusters: Detection and
Inference. Statistics in Medicine, 14:799–810, 1995.
[70] Sukhamay Kundu. Gravitational clustering: a new approach based on the
spatial distribution of the points. Pattern Recognition, 32(7):1149–1160, 1999.
[71] P. .C. Lai, C. M. Wong, A. J. Hedley, S. V. Lo, P. Y. Leung, J. Kong, and
G. M. Leung. Understanding the spatial clustering of severe acute respiratory
syndrome (sars) in hong kong. Environ Health Perspectives, 112(15):1550–
1556, 2004.
100
[72] Andrew B. Lawson, Silvia Simeon, Martin Kulldorff, Annibale Biggeri, and
Corrado Magnani. Line and point cluster models for spatial health data.
Comput. Stat. Data Anal., 51(12):6027–6043, 2007.
[73] D. D. Lee and H. S. Seung. Learning the parts of objects by non-negative
matrix factorization. Nature, 401(6755):788–791, October 1999.
[74] John Lee and Michel Verleysen.
Springer, 2007.
Nonlinear Dimensionality Reduction.
[75] Cheng-Ru Lin and Ming-Syan Chen. A robust and efficient clustering algorithm based on cohesion self-merging. In KDD ’02: Proceedings of the
eighth ACM SIGKDD international conference on Knowledge discovery and
data mining, pages 582–587, New York, NY, USA, 2002. ACM.
[76] King Ip Lin, H. V. Jagadish, and Christos Faloutsos. The tv-tree: an index
structure for high-dimensional data. The VLDB Journal, 3(4):517–542, 1994.
[77] S. Lloyd. Least squares quantization in pcm. Technical Note, Bell Laboratories.
Information Theory, IEEE Transactions on, 28(2):129–137, 1957,1982.
[78] Yaniv Loewenstein, Elon Portugaly, Menachem Fromer, and Michal Linial. Efficient algorithms for accurate hierarchical clustering of huge datasets: tackling
the entire protein space. Bioinformatics, 24(13):41–49, July 2008.
[79] G.E. Lowitz. What the fourier transform can really bring to clustering. Pattern
Recognition, 17(6):657–665, 1984.
[80] Ulrike Luxburg. A tutorial on spectral clustering. Statistics and Computing,
17(4):395–416, 2007.
[81] C. Manning, P. Raghavan, and H. Schutze. Introduction to Information Retrieval. Cambridge University, 2008.
[82] Ujjwal Maulik and Sanghamitra B. Genetic algorithm-based clustering technique. Pattern Recognition, 33:1455–1465, 2000.
[83] M. Meila and J. Shi. A random walks view of spectral segmentation. In AI
and Statistics (AISTATS), 2001.
[84] Harvey J. Miller and Jiawei Han. Geographic Data Mining and Knowledge
Discovery. Taylor & Francis, Inc., Bristol, PA, USA, 2001.
[85] Masatoshi Nei and Sudhir Kumar. Molecular Evolution and Phylogenetics.
Oxford University Press, USA, 2000.
[86] Daniel B. Neill and Andrew W. Moore. A fast multi-resolution method for
detection of significant spatial disease clusters. In Advances in Neural Information Processing Systems 16, 2003.
101
[87] Jr Newton Da Costa, Jefferson Cunha, Sergio Da Silva M. Wedel, and
J. Steenkamp. Stock selection based on cluster analysis. Economics Bulletin,
13(1):1–9, 2005.
[88] A. Y. Ng, M. Jordan, and Y. Weiss. On spectral clustering: Analysis and an
algorithm. In Advances in Neural Information Processing Systems 14, 2001.
[89] Mary K. Obenshain. Application of data mining techniques to healthcare
data. Infection Control and Hospital Epidemiology, 25:690–695, 2004.
[90] A. Okabe, B. Boots, and K. Sugihara. Spatial Tessellations: Concepts and
Applications of Voronoi Diagrams. John Wiley & Sons, 1992.
[91] Stephan Olariu and Albert Y. Zomaya. Handbook Of Bioinspired Algorithms
And Applications (Chapman & Hall/CRC Computer & Information Science).
Chapman & Hall/CRC, 2005.
[92] Clark F. Olson. Parallel algorithms for hierarchical clustering. Parallel Computing, 21(8):1313–1325, 1995.
[93] Yen-Jen Oyang, Chien-Yu Chen, and Tsui-Wei Yang. A study on the hierarchical data clustering algorithm based on gravity theory. In PKDD ’01:
Proceedings of the 5th European Conference on Principles of Data Mining and
Knowledge Discovery, pages 350–361, 2001.
[94] Lance Parsons, Ehtesham Haque, and Huan Liu. Subspace clustering for high
dimensional data: a review. SIGKDD Explor. Newsl., 6(1):90–105, 2004.
[95] L. F. Pineda-Martinez and N. Carbajal. Climatology of Mexico: a Description
Based on Clustering Analysis. American Geophysical Union Spring Meeting
Abstracts, pages A7+, May 2007.
[96] Girish Punj and David W. Stewart. Cluster analysis in marketing research:
Review and suggestions for application. Journal of Marketing Research,
20(2):134–148, May, 1983.
[97] J. Rissanen. Modeling by shortest data description. Automatica, 14:465–471,
1978.
[98] Joseph Lee Rodgers and W. Alan Nicewander. Thirteen ways to look at the
correlation coefficient. The American Statistician, 42(1):59–66, 1988.
[99] Sam T. Roweis and Lawrence K. Saul. Nonlinear dimensionality reduction by
locally linear embedding. Science, 290(5500):2323–2326, December 2000.
[100] J.-R. Sack and J. Urrutia. Handbook of computational geometry. NorthHolland Publishing Co., Amsterdam, The Netherlands, 2000.
102
[101] Sriparna Saha and Sanghamitra Bandyopadhyay. Application of a new
symmetry-based cluster validity index for satellite image segmentation. IEEE
Geoscience and Remote Sensing Letters, 5(2):166–170, 2008.
[102] Michael J. Shaw, Chandrasekar Subramaniam, Gek Woo Tan, and Michael E.
Welge. Knowledge management and data mining for marketing. Decision
Support Systems, 31(1):127–137, 2001.
[103] J. Shawe-Taylor and N. Cristianini. Kernel Methods for Pattern Analysis.
Cambridge University Press, 2004.
[104] Gholamhosein Sheikholeslami, Surojit Chatterjee, and Aidong Zhang.
WaveCluster: A multi-resolution clustering approach for very large spatial
databases. In 24th Int. Conf. Very Large Data Bases, VLDB, pages 428–439,
24–27 1998.
[105] Jianbo Shi and Jitendra Malik. Normalized cuts and image segmentation.
IEEE Transactions on Pattern Analysis and Machine Intelligence, 22(8):888–
905, 2000.
[106] R. Sibson. Slink: An optimally efficient algorithm for the single-link cluster
method. The Computer Journal, 16(1):30–34, 1973.
[107] C. Spearman. The proof and measurement of association between two things.
The American journal of psychology, 100(3-4):441–471, 1987.
[108] Daniel A. Spielman and Nikhil Srivastava. Graph sparsification by effective
resistances. In STOC ’08: Proceedings of the 40th annual ACM symposium
on Theory of computing, pages 563–568, New York, NY, USA, 2008. ACM.
[109] M. Steinbach, G. Karypis, and V. Kumar. A comparison of document clustering techniques, 2000.
[110] Alexander Szalay, Tamas Budavari, Andrew Connolly, Jim Gray, Takahiko
Matsubara, Adrian Pope, and Istvan Szapudi. Spatial clustering of galaxies in
large datasets. volume 4847, pages 1–12. Proceedings- SPIE The International
Society for Optical Engineering, 2002.
[111] Pang-Ning Tan, Michael Steinbach, and Vipin Kumar. Introduction to Data
Mining. Addison Wesley, 2005.
[112] Yufei Tao, Ke Yi, Cheng Sheng, and Panos Kalnis. Quality and efficiency
in high dimensional nearest neighbor search. In SIGMOD ’09: Proceedings
of the 35th SIGMOD international conference on Management of data, pages
563–576, New York, NY, USA, 2009. ACM.
[113] Stijn Van Dongen. Graph clustering via a discrete uncoupling process. SIAM
J. Matrix Anal. Appl., 30(1):121–141, 2008.
103
[114] Dorothea Wagner and Frank Wagner. Between min cut and graph bisection.
In MFCS ’93: Proceedings of the 18th International Symposium on Mathematical Foundations of Computer Science, pages 744–750, London, UK, 1993.
Springer-Verlag.
[115] Wei Wang, Jiong Yang, and Richard R. Muntz. Sting: A statistical information grid approach to spatial data mining. In VLDB ’97: Proceedings of the
23rd International Conference on Very Large Data Bases, pages 186–195, San
Francisco, CA, USA, 1997. Morgan Kaufmann Publishers Inc.
[116] Xin Wang and Howard J. Hamilton. DBRS: A density-based spatial clustering
method with random sampling. In Proceedings of the Seventh Pacific-Asia
Conference on Knowledge Discovery and Data Mining, pages 563–575, 2003.
[117] M. Wedel and J. Steenkamp. A clusterwise regression method for simultaneous
fuzzy market structuring and benefit segmentation. Journal of Marketing
Research, pages 385–396, 1991.
[118] Michel Wedel and Wagner A. Kamakura. Market Segmentation: Conceptual
and Methodological Foundations. Kluwer Academic Publisher, 2000.
[119] Ron Wehrens, Lutgarde M.C. Buydens, Chris Fraley, and Adrian E. Raftery.
Model-based clustering for image segmentation and large datasets via sampling. Journal of Classification, 21(2):231–253, September 2004.
[120] Li Wei, Eamonn J. Keogh, and Xiaopeng Xi. Saxually explicit images: Finding
unusual shapes. In ICDM, pages 711–720. IEEE Computer Society, 2006.
[121] W. E. Wright. Gravitational clustering. Pattern Recognition, 9(3):151–166,
1977.
[122] Xindong Wu, Vipin Kumar, J. Ross Quinlan, Joydeep Ghosh, Qiang Yang,
Hiroshi Motoda, Geoffrey J. McLachlan, Angus Ng, Bing Liu, Philip S. Yu,
Zhi-Hua Zhou, Michael Steinbach, David J. Hand, and Dan Steinberg. Top 10
algorithms in data mining. Knowledge and Information Systems, 14(1):1–37,
2007.
[123] Dragomir Yankov, Eamonn J. Keogh, Li Wei, Xiaopeng Xi, and Wendy L.
Hodges. Fast best-match shape searching in rotation invariant metric spaces.
SDM.
[124] L. Zelnik-Manor and P. Perona. Self-tuning spectral clustering. In 18th Annual
Conference on Neural Information Processing Systems, 2004.
[125] Hua-Jun Zeng, Qi-Cai He, Zheng Chen, Wei-Ying Ma, and Jinwen Ma. Learning to cluster web search results. In SIGIR ’04: Proceedings of the 27th annual
international ACM SIGIR conference on Research and development in information retrieval, pages 210–217, New York, NY, USA, 2004. ACM.
104
[126] Tian Zhang, Raghu Ramakrishnan, and Miron Livny. Birch: A new data clustering algorithm and its applications. Data Mining and Knowledge Discovery,
1(2):141–182, 1997.
[127] Ying Zhao and George Karypis. Hierarchical clustering algorithms for document datasets. Data Mining and Knowledge Discovery, 10(2):141–168, 2005.
[128] Xianjin Zhu, Rik Sarkar, and Jie Gao. Shape segmentation and applications
in sensor networks. In Proceedings of the 26th IEEE International Conference
on Computer Communications, pages 1838–1846, 2007.