Download Chapter 35 – Interference and Diffraction

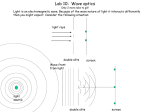
Chapter 35 – Interference
I.
Introduction – Examine some of the wave properties of light. The analysis of waves for light is similar
to the analysis of waves on a string and for sound waves, e.g., interference: constructive and
destructive.
II. Coherence of light
A.
B.
In order to have interference of light it is necessary to have at least two sources of light, and the light
must be coherent. Light from two sources is coherent if the phase difference between the two waves
is constant. For example,
source 1
source 1
source 2
source 2
How can you get coherent light?
1.
Light passing through one, then through two slits.
2.
Laser
1
II.
Interference of light due to two slits
A.
Assume the light emerging from two parallel slits are in phase. The two slits are separated by a
distance d.
S1
optic axis
S2
screen
B.
Analyze mathematically what happens when the light waves coming from the slits interferes with
each other.
P
r1
y
S1

d

r2
O
Q
S2
path
difference
R: R >> d
2
Note that the light traveling from the slits to point P on the screen travel different distances. Because
of this, there is a phase difference between the two waves at P, the resulting amplitude can vary from
zero to a maximum magnitude of two times the amplitude of the waves reaching point P.
Digress: Take a look at two waves traveling different distances, then interfering with each other.
wave
from
slit 1
wave
from
slit 2
S1
S2
Note that constructive interference occurs if the path difference = 0, 1, 2, etc., and destructive
1 3
interference occurs if the path difference =  ,  , etc. So, in our case the two situations can be
2 2
written as:
For constructive interference:
For destructive interference
3
C.
Examples
1.
In the double slit situation, light of wavelength  illuminates a set of double slits. An
interference pattern is observed on a screen that is a distance R from the slits, where R >> d.
Find the distance between two consecutive bright fringes on the screen.
d

O
R
2.
What happens to the distance between the dark or light fringes on the screen when
a.
the distance between the slits d increases or decreases?
b.
the wavelength of the illuminating light increases or decreases?
4
3.
Monochromatic light illuminates a set of double slits where the distance between the slits is 0.2
mm. On a screen that is 1.5 m from the slits, the fourth order bright fringe is 1.8 cm from the
optic axis. Find the wavelength of the light.
C: m = 5
C: m = 4
C: m = 3
C: m = 2
C: m = 1
C: m = 0
III. Look at the intensity pattern of the light on the screen due to the double slits
A.
Consider two waves that are in phase leaving the two slits and interfering with each other at point P
on the screen. The frequency and amplitude of the waves are the same. Because the waves travel
different distances to P, there will be a phase difference, , between the waves.
E1
P
E1 = E sin (t)
E2
E2 = E sin (t + )
Digression: Remember how the path difference (p.d.) between two waves relates to the phase difference
() between the two waves. (This was done when we talked about sound.)
At point P the resulting electric field and the intensity can be found.
EP = E1 + E2 = E sin t + E sin (t + )
5
Remember: Intensity  (Amplitude)2
2


So, Intensity   2 E cos  , or
2

where  
B.
I  I o cos 2

,
2
2
2 dy
d sin  
.

 R
How does the intensity vary? Graph the intensity on the screen for the following situation: light of
wavelength  = 600 nm, passes through two slits separated by a distance d = 0.2 mm, and the screen
is a distance R = 1.5 m from the slits.
Graph the intensity for phase differences  = 0 to  =  3.
+3
+2
 (rad)
(deg)
y (cm)
I (W/m2)
0
 /4
+
 /2
 3/4

I
optic
axis
Io

 3/2
 2
 5/2
 3
-
y

Digression: When looking at a real interference pattern, the intensities actually drop off as one
moves away from the optic axis. This is due to the width of the slits. The above derivation assumes
the widths of the slits are infinitesimally thin.
6
IV. Phasor method of finding the intensity
A.
Again consider the two waves leaving the slits and reaching point P on the screen:
E1 = E sin (t) and E2 = E sin (t + ) .
Think of a phasors as vectors of length E at the angles t and t .
Note that the projection of the phasors onto the vertical axis gives E1 and E2. If we add the two
phasors, we get the phasor (EP) representing the amplitude of the total electric field at point P. The
projection of this phasor onto the y-axis gives the electric field at point P.
EP is the resultant phasor (vector), and its value can be found most easily by rotating the axes until
the first phasor lies on the x-axis. (The value of t is arbitrary, so the diagram with rotated axes can
be drawn by setting t = 0.)
EP represents the resultant amplitude of the waves reaching point P from the two slits.
7
The value of EP can easily be found:
B.
Because the intensity of the light at point P is proportional to the square of the amplitude, the
intensity can be written as:
Note that the phase angles corresponding to maximum and minimum intensities can easily be found
dI
 0.
by
d
8
V.
Thin film interference
A.
Where is it observed?
1.
colors on the surface of water on the street
2.
nonreflective coating on lenses
3.
iridescence of feathers and on insects
4.
B.
Thin film interference is due to the interference of light reflecting from the two surfaces of a thin film.
light source
top
surface
thin
film
bottom
surface
C.
Analyze – simplify by looking at monochromatic light hitting a surface at normal incidence. Look at
a thin wedge of water (soap film) where the thickness is very thin. What kind of interference occurs
at the top? Why?
water
9
Digress: phase shifts at boundaries of a string – fixed and free.
What are the boundary conditions for light? Look at the Lloyd’s mirror experiment.
light source
glass
screen
Conclusion: If light waves are traveling in one medium and are reflected from the surface of a
medium with a lower index, no phase shift occurs. If the reflecting medium has a higher index, then
a 180o phase shift occurs.
10
D.
Expressions for constructive and destructive interference. (we are assuming the light is incident
normally on the thin film.)
n1
n
t
n2
n1 > n and n > n2
n1 < n and n < n2
n1 > n and n < n2
n1 < n and n > n2
11
E.
Examples
1.
Monochromatic light of wavelength 500 nm is incident normally on two glass plates that are in
contact at one end and separated by a 4 m thick hair at the other end.
4 m
2.
a.
Is the point of contact (or close to the point of contact) a point where constructive or
destructive interference occurs?
b.
How many dark (destructive interference) lines are present over the length of the glass
plates?
Find the minimum thickness of a material with index 1.30 to produce a coating on a glass (n =
1.50) lens so that it is not reflecting? What is the color of the reflected light? What is the color of
the transmitted light?
12
3.
Newton’s rings occur when a curved surface is placed on a flat plate.
R
4.
The interferometer
light
source
observer
13